Logarithmusfunktionen
Logarithmengesetze, Umkehrfunktion, Definitionsbereich, Wertebereich, Eigenschaften
Inhaltsverzeichnis zum Thema
- Was ist der Logarithmus?
- Die allgemeine Logarithmusfunktion
- Der Definitionsbereich
- Der Wertebereich
- Spezielle Funktionswerte und Grenzwertverhalten
- Beispiel
- Einfluss der Basis auf den Funktionsgraphen
- Die natürliche Logarithmusfunktion
Was ist der Logarithmus?
Der Logarithmus ist die Umkehroperation zum Potenzieren.
Wir beginnen mit einem Beispiel.
- Du weißt sicherlich, dass $3^4 = 3 \cdot 3 \cdot 3 \cdot 3 =81$ ist.
- Wenn du nun umgekehrt wissen möchtest, mit welcher Zahl du $3$ potenzieren musst, um $81$ zu erhalten, wie kannst du dann vorgehen?
Diese Frage führt zu der Gleichung $3^x=81$. Hier hilft dir der Logarithmus weiter. Er beantwortet die Frage: „Mit welcher Zahl musst du $3$ potenzieren, damit $81$ herauskommt?“
Die Lösung lautet $x=\log_3{81}$.
Allgemeiner kannst du dies auch so formulieren:
- Die Gleichung $a^x=b$ wird durch $y=\log_a{b}$ gelöst.
- Der rechte Teil der Gleichung wird „Logarithmus zur Basis $a$ von $b$“ genannt.
- Dabei muss die Basis positiv sein.
Es gibt natürlich verschiedene Basen. Einige davon führen zu speziellen Logarithmen, welche besonders häufig verwendet werden:
- Der Logarithmus zur Basis $10$ wird auch als dekadischer Logarithmus bezeichnet und schreibt sich abkürzend so: $\log_{10}=\lg$.
- Der Logarithmus zur Basis $e\approx2,71828$, der Euler'schen Zahl, wird als Logarithmus naturalis bezeichnet: $\log_e=\ln$.
Diese beiden Logarithmen findest du auch auf deinem Taschenrechner.
Die allgemeine Logarithmusfunktion
Eine Logarithmusfunktion zur Basis $a$ hat folgende Gestalt:
$\quad~~~f(x)=\log_a(x)$
Die Logarithmusfunktion zur Basis $a$ ist die Umkehrfunktion der Exponentialfunktion zur Basis $a$.
Der Definitionsbereich
Da der Logarithmus die Umkehroperation zum Potenzieren ist und die Basis $a$, welche potenziert wird, positiv ist, folgt daraus, dass auch $a^x$ positiv ist. Dies bedeutet, dass die Logarithmusfunktion nur für positive Argumente definiert ist:
$\quad~~~\mathbb{D}_f=\mathbb{R}^+$
Der Wertebereich
Der Wertebereich der Logarithmusfunktion ist die Menge der reellen Zahlen:
$\quad~~~\mathbb{W}_f=\mathbb{R}$
Spezielle Funktionswerte und Grenzwertverhalten
- Es ist $f(1)=\log_a(1)=0$. Den Punkt $P(1|0)$ haben alle Exponentialfunktionen unabhängig von der Basis gemeinsam, da $a^0=1$ gilt.
- Wenn du für $x=a$ einsetzt, erhältst du $f(a)=\log_a(a)=1$, da $a^1=a$ ist.
Diese beiden Funktionswerte hat jede Logarithmusfunktion unabhängig von der Basis $a>0$, $a\neq 0$. Bei den Grenzwerten werden zwei Fälle unterschieden.
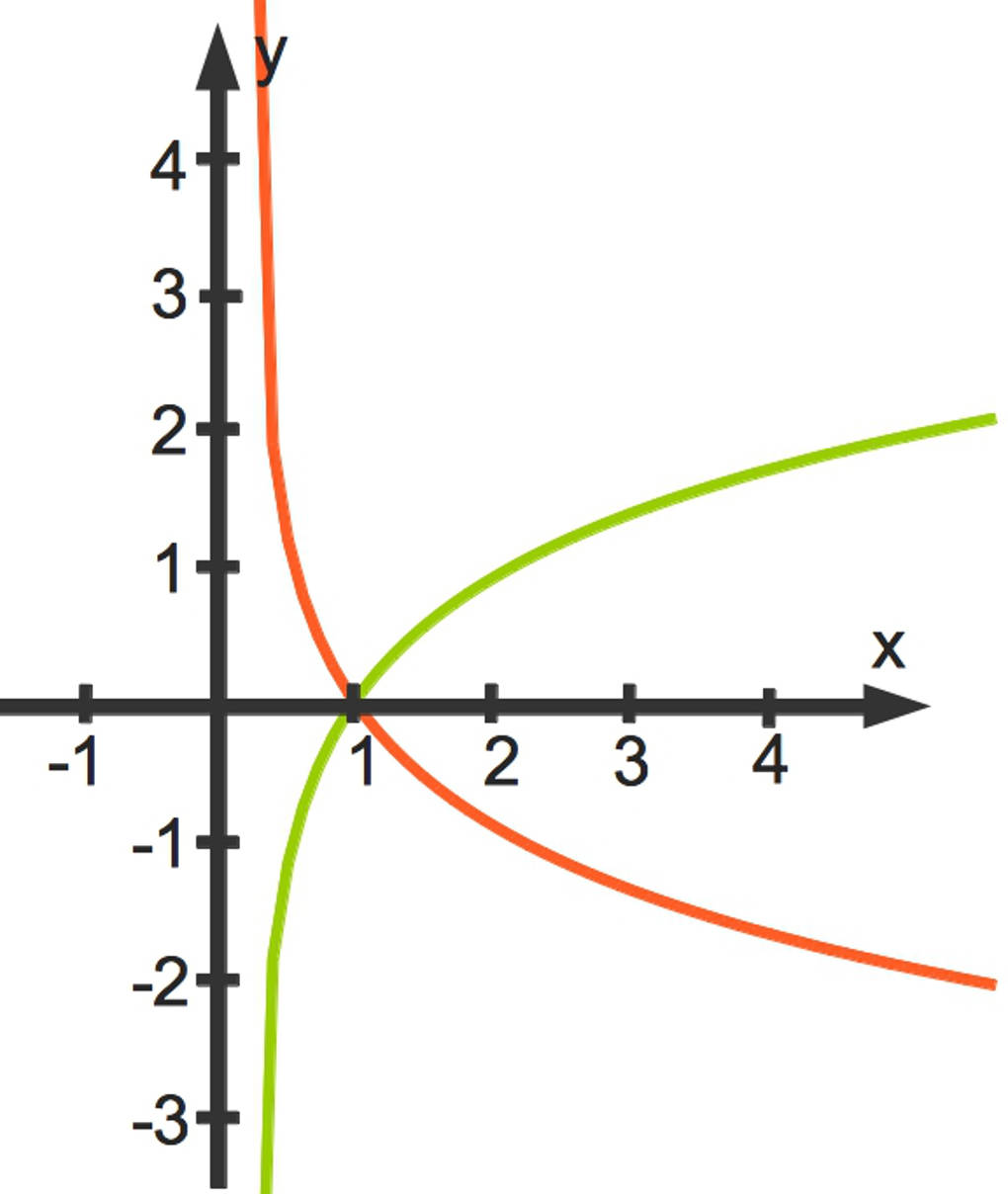
Erster Fall: $f(x)=\log_a(x)$, für $a>1$
- $\lim\limits_{x\to 0}f(x)=$„$-\infty$“ sowie
- $\lim\limits_{x\to \infty}f(x)=$„$\infty$“.
Zweiter Fall: $g(x)=\log_a(x)$, für $0 < a < 1$
$\lim\limits_{x\to 0}g(x)=$„$\infty$“ sowie
$\lim\limits_{x\to \infty}g(x)=$„$-\infty$“.
Hier siehst die Funktionsgraphen zu $f(x)=\log_2(x)$ (grün) und den zu $g(x)=\log_{0,5}(x)$ (rot).
Beispiel
Wir untersuchen folgende Funktion:
$f(x)=\log_{1,2}(x)-17,65$
Dabei steht $x$ für die Anzahl von Menschen, die eine Neuigkeit erfahren haben, und $f(x)$ für die Zeit in Tagen, zu der diese Neuigkeit so viele Menschen erreicht hat.
- Willst du wissen, nach wie vielen Tagen $100$ Menschen die Neuigkeit kennen, setzt du $x=100$ in die Funktionsgleichung ein:
$\quad~~~f(100)=\log_{1,2}(100)-17,65\approx 7,6$
- Nach etwas mehr als siebeneinhalb Tagen kennen $100$ Menschen die Neuigkeit.
- Möchtest du wissen, wie viele Menschen die Neuigkeit am Anfang, also $f(x)=0$, kennen, musst du eine Gleichung lösen:
$\quad~~~\begin{array}{rclll}0&=&\log_{1,2}(x)-17,65&|&+17,65\\ 17,65&=&\log_{1,2}(x)&|&1,2^{(~~~)}\\ 1,2^{17,65}&=&x\\ 25&\approx&x \end{array}$
- Zu Beginn kennen $25$ Menschen die Neuigkeit.
- Übrigens: Die zugehörige Exponentialfunktion lautet wie folgt:
$\quad~~~g(x)=25\cdot 1,2^x$
Einfluss der Basis auf den Funktionsgraphen
Bei der Exponentialfunktion $g(x)=a^x$ kannst du feststellen, dass diese umso steiler verläuft, je größer die Basis $a$ ist. Umgekehrt verläuft die entsprechende Logarithmusfunktion flacher.
Die natürliche Logarithmusfunktion
Die natürliche Logarithmusfunktion $f(x)=\ln(x)$ ist die Umkehrfunktion der natürlichen Exponentialfunktion $g(x)=e^x$.
Auch bei der natürlichen Logarithmusfunktion ist der Definitionsbereich $\mathbb{D}_f=\mathbb{R}^+$ und der Wertebereich $\mathbb{W}_f=\mathbb{R}$.
Beispiel
Wir schauen uns folgende Funktion an:
$\quad~~~f(x)=3\ln(x-1)-2$
Wir untersuchen erst einmal, für welche Argumente $x$ die Funktion überhaupt definiert ist. Es muss $x-1>0$ gelten, also $x>1$. Damit ist $\mathbb{D}_f=\{x\in\mathbb{R}:x>1\}$.
Du kannst den Funktionsgraphen zeichnen, indem du eine Wertetabelle erstellst:

Den zugehörigen Funktionsgraphen kannst du hier sehen.
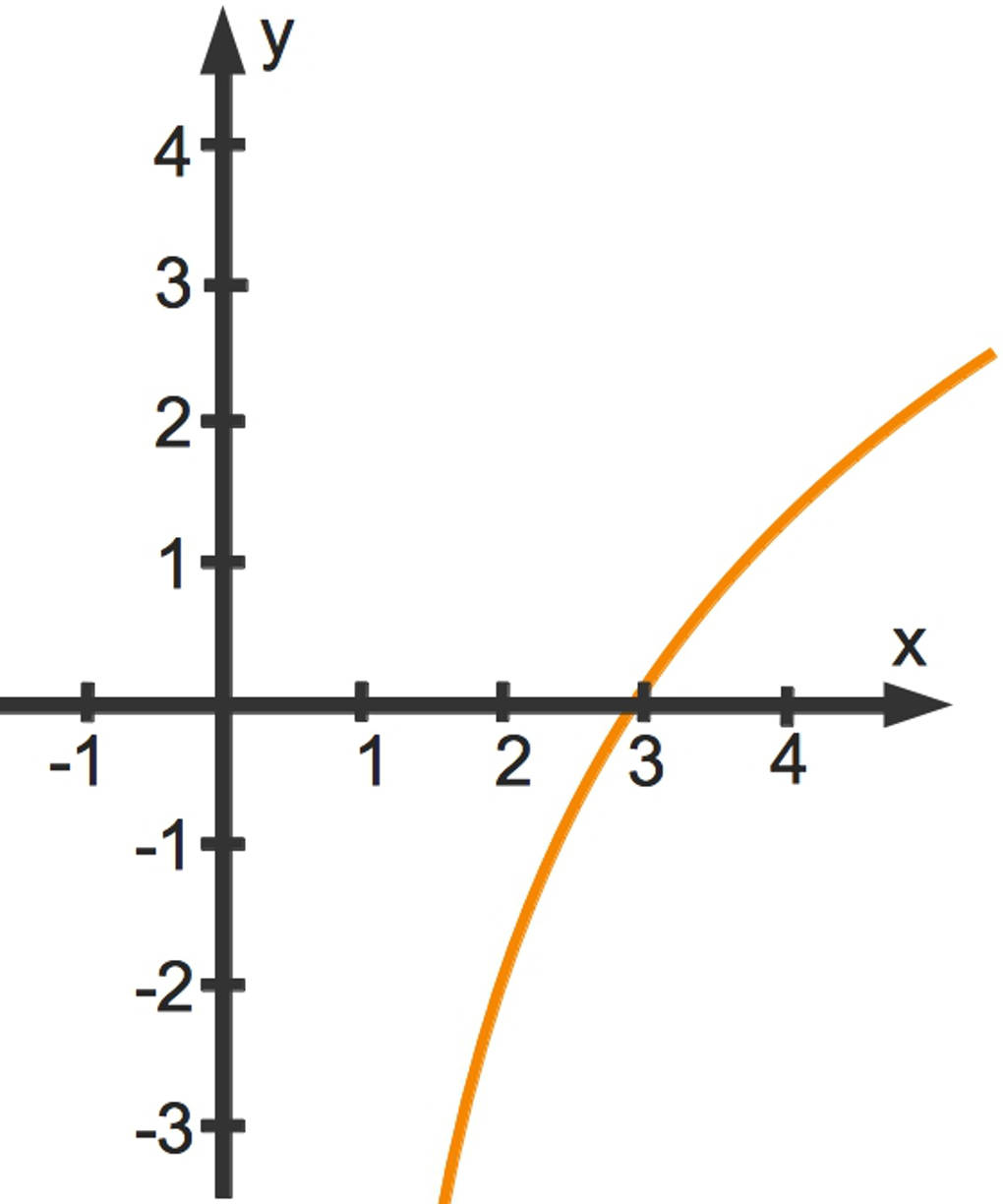
Nun kannst du dich auch fragen, für welches $x$ der Funktionswert $f(x)=19$ angenommen wird. Dies führt zu einer Gleichung $19=3\ln(x-1)-2$, deren Lösung du hier siehst:
$\quad~~~\begin{array}{rclll} 19&=&3\ln(x-1)-2&|&+2\\ 21&=&3\ln(x-1)&|&:3\\ 7&=&\ln(x-1)&|&e^{(~~~)}\\ e^7&=&x-1&|&+1\\ e^7+1&=&x\\ 1097,6&\approx&x \end{array}$
Bei den allgemeinen Logarithmusfunktionen ist bereits das Grenzwertverhalten erklärt worden. An diesem Beispiel kannst du erkennen, dass die Logarithmusfunktion „sehr langsam“ gegen $\infty$ geht.
Alle Videos zum Thema
Videos zum Thema
Logarithmusfunktionen (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Logarithmusfunktionen (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Exponentialfunktion Beispiel



 Logarithmusfunktion
Logarithmusfunktion









