Ganzrationale Funktionen – Rekonstruktion
Weißt du bereits, wie du von einer ganzrationalen Funktionsgleichung zu dem Funktionsgraphen kommst? Hierfür führst du eine Kurvendiskussion. Umgekehrt kannst du auch die Funktionsgleichung rekonstruieren.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was sind ganzrationale Funktionen?
- Was ist eine Rekonstruktion?
- Vorgehensweise bei der Rekonstruktion
- Bekannt: Punkte des Funktionsgraphen
- Bekannt: Die Steigung an einer Stelle
- Bekannt: Wendestelle oder Wendepunkt des Funktionsgraphen
- Bekannt: Symmetrie
- Die Rekonstruktion am Beispiel
Was sind ganzrationale Funktionen?
Eine ganzrationale Funktion ist eine Funktion, deren Funktionsgleichung diese Form hat:
$f(x)=a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+\dots +a_2x^2+a_1x+a_0$.
Dabei wird festgelegt, dass $a_n$ nicht den Wert $0$ haben darf. Man schreibt dafür $a_n\neq 0$ .
- Der Grad dieser Funktion wird durch den höchsten Exponenten festgelegt. Dieser ist $n$.
- Die Werte $a_n$, ..., $a_2$, $a_1, a_0$ sind die Koeffizienten des Polynoms.
Oft wirst du eine solche Funktion untersuchen und bestimmte Eigenschaften bzw. wichtige Punkte und Stellen der Funktion ermitteln müssen. Eine solche Untersuchung wird Kurvendiskussion genannt. Bei dieser bestimmst du bei einer gegebenen Funktionsgleichung Nullstellen, Extrema und Wendepunkte des zugehörigen Funktionsgraphen. Weiterhin kannst du den Funktionsgraphen auf Symmetrie untersuchen. Wenn du all diese Ergebnisse in ein Koordinatensystem einträgst, erhältst du eine Skizze des Funktionsgraphen.
In diesem Text lernst du genau die umgekehrte Richtung kennen.
Was ist eine Rekonstruktion?
Bei einer Rekonstruktion benutzt du gegebene Informationen (z.B. Symmetrie, Position von Nullstellen etc.) über eine Funktion, um die Funktionsgleichung zu rekonstruieren. Oft musst du bei einer solchen Aufgabe die Informationen aus einem kurzen Text ermitteln.
Solche Aufgaben werden auch Steckbriefaufgaben genannt, da wie bei einem Steckbrief Eigenschaften genutzt werden, um etwas (hier eine Funktionsgleichung) zu finden.
Im Folgenden schauen wir uns an, wie du Informationen aus einer solchen Steckbriefaufgabe in mathematische Gleichungen übersetzen kannst. Abschließend siehst du an einem Beispiel, wie eine Rekonstruktion durchgeführt wird.
Vorgehensweise bei der Rekonstruktion
Die wichtigste Information ist der Grad $n$ der gesuchten Funktion, da du mit Hilfe von diesem die allgemeine Funktionsgleichung aufstellen kannst. Merke dir folgende Begriffe zu ganzrationalen Funktionen, da diese häufig in Aufgabenstellungen vorkommen:
- Eine lineare Funktion ist eine Funktion der Form $f(x)=mx+n$. Bei diesen musst du $m$ und $n$ ermitteln. Sie hat den Grad $1$.
- Eine quadratische Funktion hat die Form $f(x)=ax^2+bx+c$. Hier musst du $a$, $b$ und $c$ ermitteln. Sie hat den Grad $2$.
- Eine kubische Funktion hat die Form $f(x)=ax^3+bx^2+cx+d$. Hier musst du $a$, $b$, $c$ und $d$ ermitteln. Sie hat den Grad $3$.
Auch für die nachfolgenden Grade gibt es noch Bezeichnungen, die aber seltener verwendet werden. Ein Spezialfall sind sogenannte biquadratische Funktionen. Diese haben die Form $f(x)=ax^4+bx^2+c$ und somit den Grad $4$.
Nachdem du die Funktionsgleichung der gesuchten Funktion in allgemeiner Form aufgestellt hast, musst du die gegebenen Bedingungen nutzen. Du brauchst immer mindestens so viele Bedingungen, wie du Unbekannte herausfinden willst. Wenn du eine ganzrationale Funktion vom Grad $n$ suchst, benötigst du $n+1$ Bedingungen.
Je nachdem, welche Bedingungen du gegeben hast, ändert sich dein Vorgehen.
Nun kannst du mit der Rekonstruktion von ganzrationalen Funktionen beginnen.
Bekannt: Punkte des Funktionsgraphen
Jeder Punkt $P(p_x|p_y)$, der auf dem Graphen einer Funktion $f$ liegt, erfüllt $f(p_x)=p_y$. Wenn du also die $x$-Koordinate des Punktes in die Funktionsgleichung einsetzt, erhältst du dessen $y$-Koordinate. Beispielsweise führt der Punkt $P(3|6)$ zu der Gleichung $f(3)=6$.
Dies gilt auch für die Schnittpunkte mit den Koordinatenachsen:
- Eine Schnittstelle $x_N$ mit der $x$-Achse führt zu der Gleichung $f(x_N)=0$.
- Die Schnittstelle $y_S$ führt zu $f(0)=a_0=y_S$. Eine solche Schnittstelle ist besonders praktisch bei Steckbriefaufgaben, da du direkt $a_0$ erhältst.
Bekannt: Die Steigung an einer Stelle
Wenn du aus der Aufgabe weißt, dass der Graph zum Beispiel bei $x=3$ die Steigung $5$ hat, gilt $f'(3) = 5$. Beachte, dass hier die erste Ableitung genutzt wird.
Dies gilt auch für Extremstellen. Bei diesen ist die Steigung immer $0$.
Beachte: Eine Extremstelle ist die $x$-Koordinate eines Extrempunktes.
Ein gegebener Extrempunkt beinhaltet also direkt zwei nutzbare Informationen. Dies siehst du hier in einem Beispiel:
„Der Funktionsgraph der Funktion $f$ hat einen Tiefpunkt bei $(1|4)$.“
Dies führt dich zu den Gleichungen $f(1)=4$ und $f'(1)=0$.
Bekannt: Wendestelle oder Wendepunkt des Funktionsgraphen
Die Vorgehensweise ist wie bei Extremstellen bzw. -punkten mit dem Unterschied, dass du die zweite Ableitung nutzen musst.
Bekannt: Symmetrie
Bei ganzrationalen Funktionen kannst du die Symmetrie mit Hilfe der Exponenten untersuchen:
- Wenn alle Exponenten gerade sind, ist die Funktion achsensymmetrisch zur $y$-Achse.
- Sind alle Exponenten ungerade, ist die Funktion punktsymmetrisch zum Koordinatenursprung.
Wenn du also eine der beiden genannten Symmetrien kennst, kannst du bereits einige Summanden in der ganzrationalen Funktion streichen.
All diese Eigenschaften ganzrationaler Funktionen kannst du dir übersichtlich in einer Tabelle zusammenfassen.
Die Rekonstruktion am Beispiel
Schau dir nun ein Beispiel zur Rekonstruktion ganzrationaler Funktionen an.
Gesucht ist eine ganzrationale, kubische Funktion $f$. Der Graph dieser Funktion hat einen lokalen Hochpunkt $\text{HP}(-1|4)$ und schneidet die Koordinatenachsen bei $x=-2$ und $y=2$. Hier siehst du diese Informationen in einem Koordinatensystem:
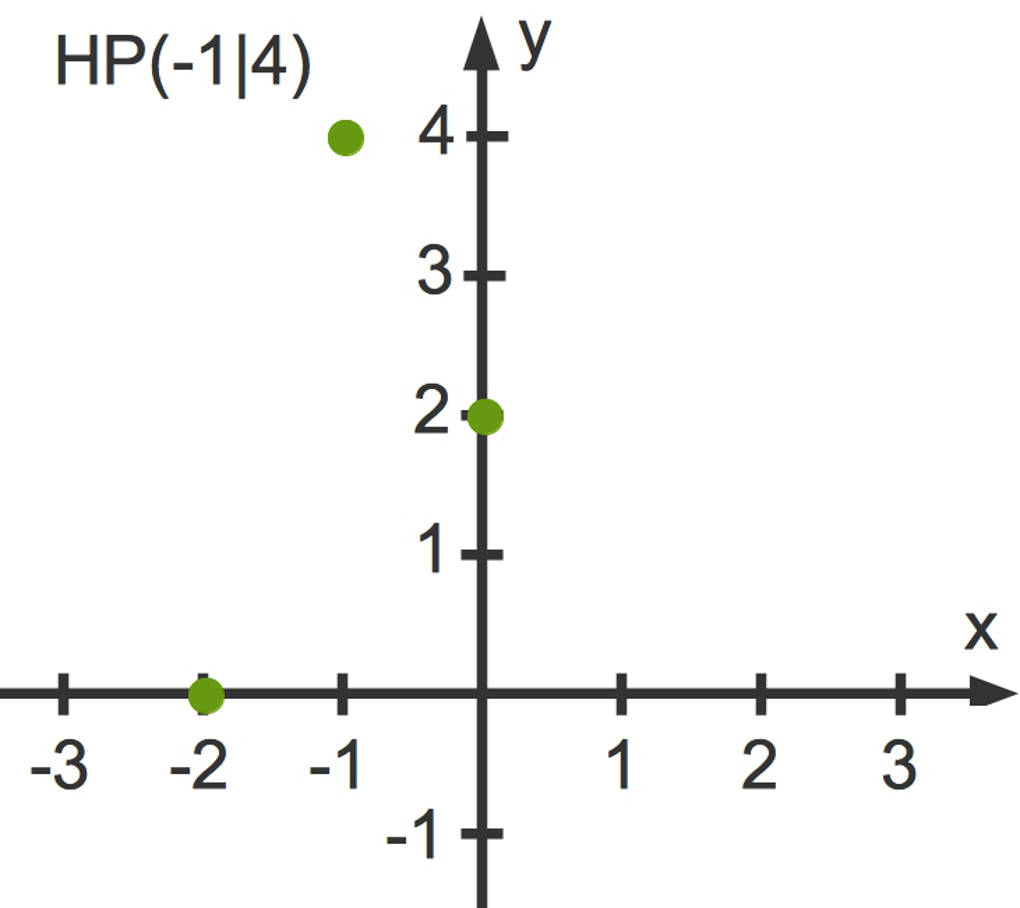
Da die gesuchte Funktion kubisch ist, lautet die allgemeine Funktionsgleichung $f(x)=ax^3+bx^2+cx+d$. Da ein lokales Extremum bekannt ist, benötigst du auch noch die erste Ableitung. Diese lautet $f'(x)=3ax^2+2bx+c$.
Nun schauen wir uns die einzelnen Informationen an und halten fest, was du daraus ableiten kannst:
- Der Graph hat eine Schnittstelle mit der $y$-Achse bei $y=2$. Es gilt $f(0) = 2$. Da alle Summanden bis auf $d$ auf diese Weise „wegfallen“, erhältst du $d=2$.
- Da $f(-2)=0$ ist, erhältst du die Gleichung $-8a+4b-2c+2=0$.
- Der Hochpunkt liefert $f(-1)=4$, also $-a+b-c+2=4$ und $f'(-1)=0$, also $3a-2b+c=0$.
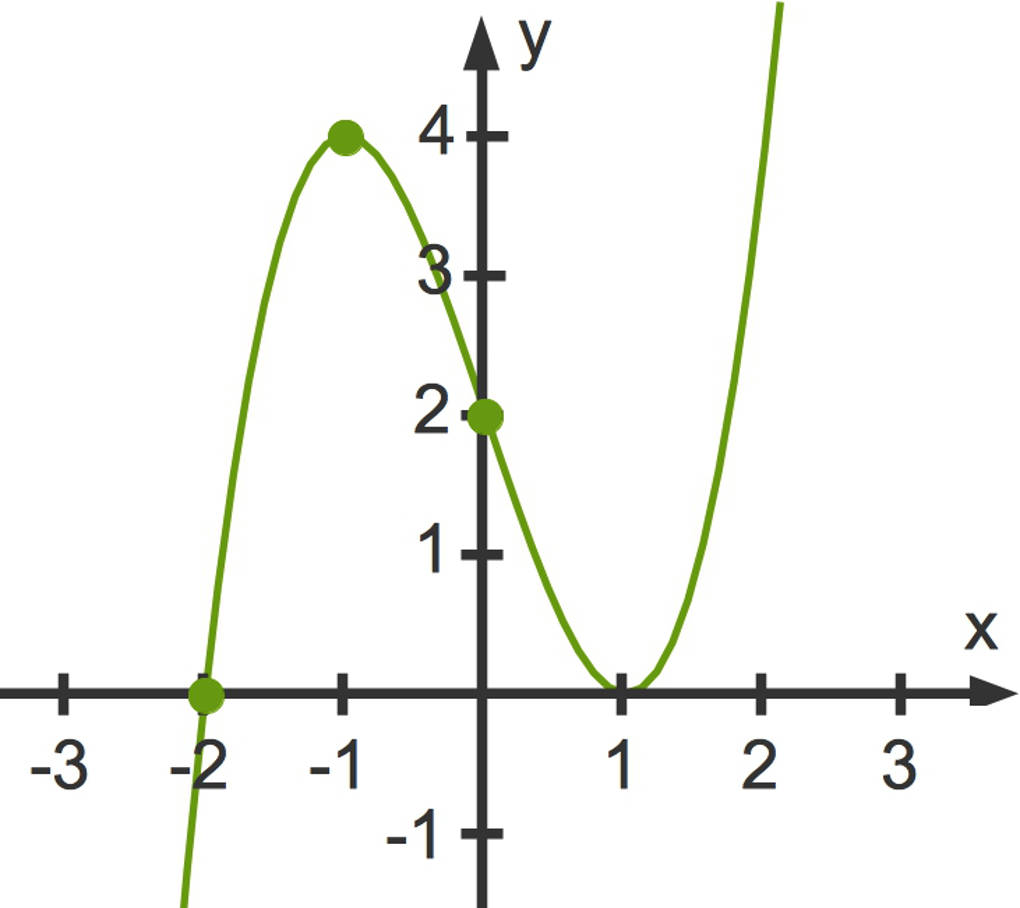
Die drei letzten Gleichungen bilden ein lineares Gleichungssystem. Wenn du dieses Gleichungssystem löst, erhältst du die Werte $a=1$, $b=0$ und $c=-3$. Die gesuchte Funktion $f$ hat also die Funktionsgleichung $f(x)=x^3-3x+2$. Du hast nun eine Funktion dritten Grades rekonstruiert.
Hier kannst du den zugehörigen Funktionsgraphen sehen:
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Ganzrationale Funktionen – Rekonstruktion (3 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Ganzrationale Funktionen – Rekonstruktion (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze







 Rekonstruktion ganzrationaler Funktionen – Lösungsstrategie
Rekonstruktion ganzrationaler Funktionen – Lösungsstrategie
 Rekonstruktion ganzrationaler Funktionen – Übersicht Eigenschaften
Rekonstruktion ganzrationaler Funktionen – Übersicht Eigenschaften
 Rekonstruktion ganzrationaler Funktionen – Rutsche
Rekonstruktion ganzrationaler Funktionen – Rutsche
 Rekonstruktion ganzrationaler Funktionen – Pipeline
Rekonstruktion ganzrationaler Funktionen – Pipeline









