Winkelfunktionen und Einheitskreis
Einfach lernen mit Videos, Übungen, Aufgaben & Arbeitsblättern
Inhaltsverzeichnis zum Thema
- Der Einheitskreis
- Der Sinus am Einheitskreis
- Der Cosinus am Einheitskreis
- Der Tangens am Einheitskreis
- Das Bogenmaß
- Was sind Polarkoordinaten?
Der Einheitskreis
Der Einheitskreis ist ein spezieller Kreis. Der Radius des Einheitskreises ist $r=1$.

Mit Hilfe dieses Einheitskreises können die Winkelfunktionen Sinus, Cosinus sowie Tangens erklärt werden.
In dem rechtwinkligen Dreieck ist der Radius $r$ die Hypotenuse. Somit ist
$\sin(x)=\frac{\text{Gegenkathete von }\alpha}{r}=\text{Gegenkathete von }\alpha$,
$\cos(x)=\frac{\text{Ankathete von }\alpha}{r}=\text{Ankathete von }\alpha$ und
$\tan(x)=\frac{\text{Gegenkathete von }\alpha}{\text{Ankathete von }\alpha}$.
Der Sinus am Einheitskreis

Wenn du den Winkel $\alpha$ veränderst, verändert sich auch der zugehörige Sinuswert.
- Für $\alpha=0^\circ$ erhältst du $\sin(\alpha)=0$.
- Für $\alpha=90^\circ$ erhältst du $\sin(\alpha)=1$.
- Für $\alpha=180^\circ$ erhältst du $\sin(\alpha)=0$.
- Für $\alpha=270^\circ$ erhältst du $\sin(\alpha)=-1$.
- Für $\alpha=360^\circ$ erhältst du $\sin(\alpha)=0$.

Von nun an wiederholen sich die Sinuswerte. Dies wird als Periodizität bezeichnet.
- Die Periodenlänge ist $360^\circ$. Das bedeutet, du kannst den Graph kopieren und rechts sowie links anhängen. Damit bekommst du den Verlauf der Sinusfunktion.
- Der Definitionsbereich von Sinus ist $\mathbb{D}_{\sin}=\mathbb{R}$.
- Der Wertebereich von Sinus ist $\mathbb{W}_{\sin}=[-1;1]$.
- Die Nullstellen von Sinus sind die ganzzahligen Vielfachen von $180^\circ$.
Der Cosinus am Einheitskreis
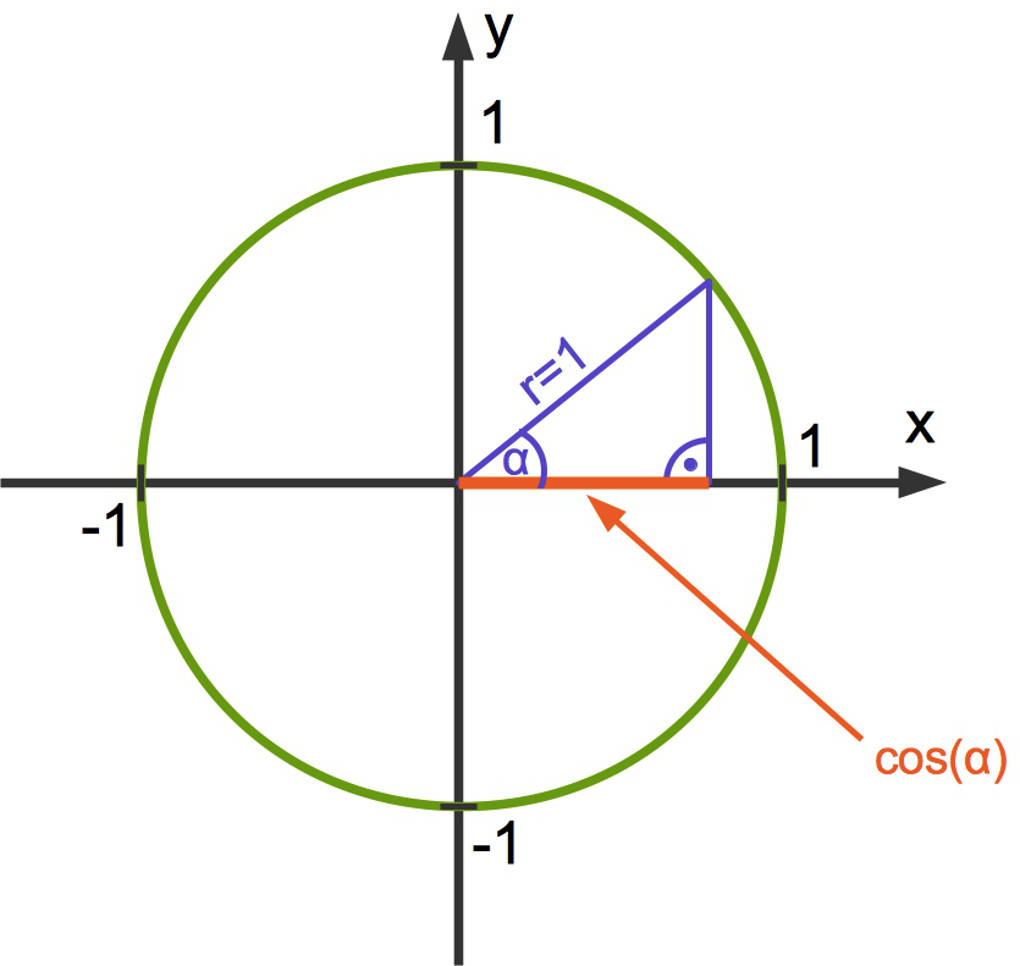
Ebenso wie beim Sinus kannst du durch Veränderung von $\alpha$ verschiedene Cosinuswerte berechnen.
- Für $\alpha=0^\circ$ erhältst du $\cos(\alpha)=1$.
- Für $\alpha=90^\circ$ erhältst du $\cos(\alpha)=0$.
- Für $\alpha=180^\circ$ erhältst du $\cos(\alpha)=-1$.
- Für $\alpha=270^\circ$ erhältst du $\cos(\alpha)=0$.
- Für $\alpha=360^\circ$ erhältst du $\sin(\alpha)=1$.
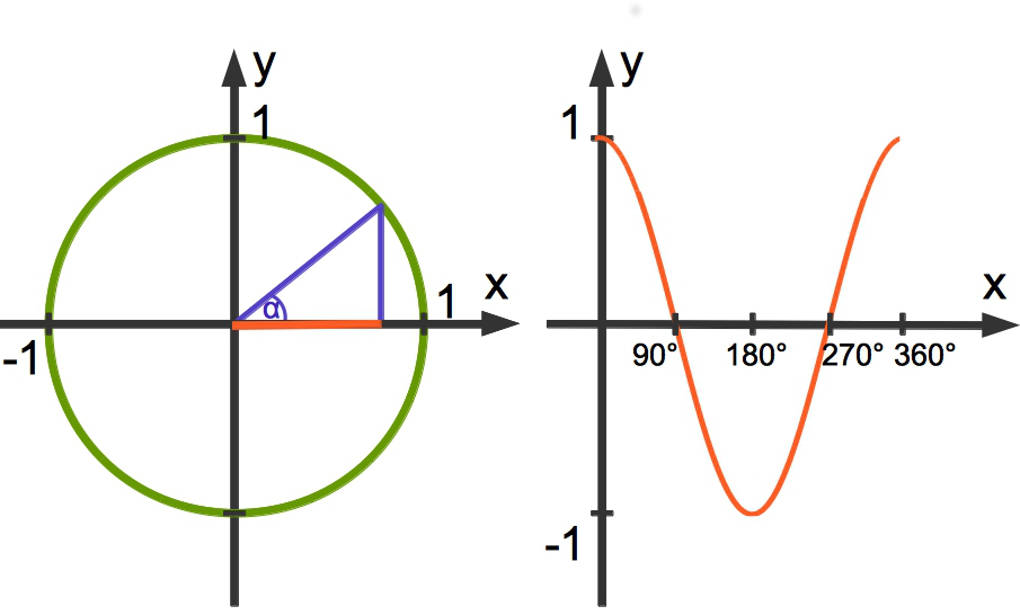
- Auch die Cosinusfunktion ist periodisch mit der Periodenlänge $360^\circ$.
- Der Definitionsbereich von Cosinus ist $\mathbb{D}_{\cos}=\mathbb{R}$.
- Der Wertebereich von Cosinus ist $\mathbb{W}_{\cos}=[-1;1]$.
- Die Nullstellen von Cosinus sind gegeben durch $90^\circ$ plus die ganzzahligen Vielfachen von $180^\circ$.
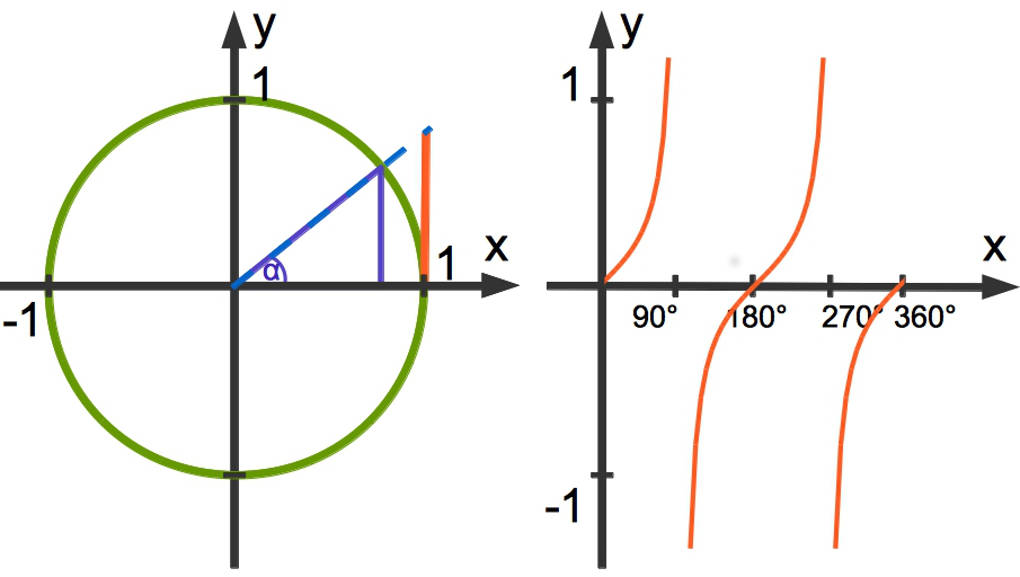
Der Tangens am Einheitskreis

- Für $\alpha=0^\circ$ erhältst du $\tan(\alpha)=0$.
- Für $\alpha=45^\circ$ erhältst du $\tan(\alpha)=1$.
- Der Tangens ist nicht definiert für $90^\circ$ plus die ganzzahligen Vielfachen von $180^\circ$.
- Der Wertebereich von Tangens ist $\mathbb{W}=\mathbb{R}$.
- Der Tangens ist periodisch mit der Periodenlänge $180^\circ$.
- Die Nullstellen des Tangens sind die ganzzahligen Vielfachen von $180^\circ$.
Das Bogenmaß
Bei den trigonometrischen Funktionen wird entweder das Winkelmaß oder das Bogenmaß verwendet. Dieses wird als Vielfaches der Kreiszahl $\pi=3,1415...$ dargestellt.
- $0^\circ~\hat=~ 0$
- $90^\circ~\hat=~ \frac{\pi}2$
- $180^\circ~\hat=~\pi$
- $270^\circ~\hat=~ \frac{3\pi}2$
- $360^\circ~\hat=~ 2\pi$
Mit dem Bogenmaß kann die Periodizität der Kreisfunktionen wie folgt erklärt werden:
- Sinus und Cosinus sind $2\pi$-periodisch und
- Tangens $\pi$-periodisch.
Was sind Polarkoordinaten?
Ein Punkt in einem kartesischen Koordinatensystem hat eine x- sowie eine y-Koordinate: $P(x|y)$. Man kann jeden Punkt auch mit Polarkoordinaten darstellen.
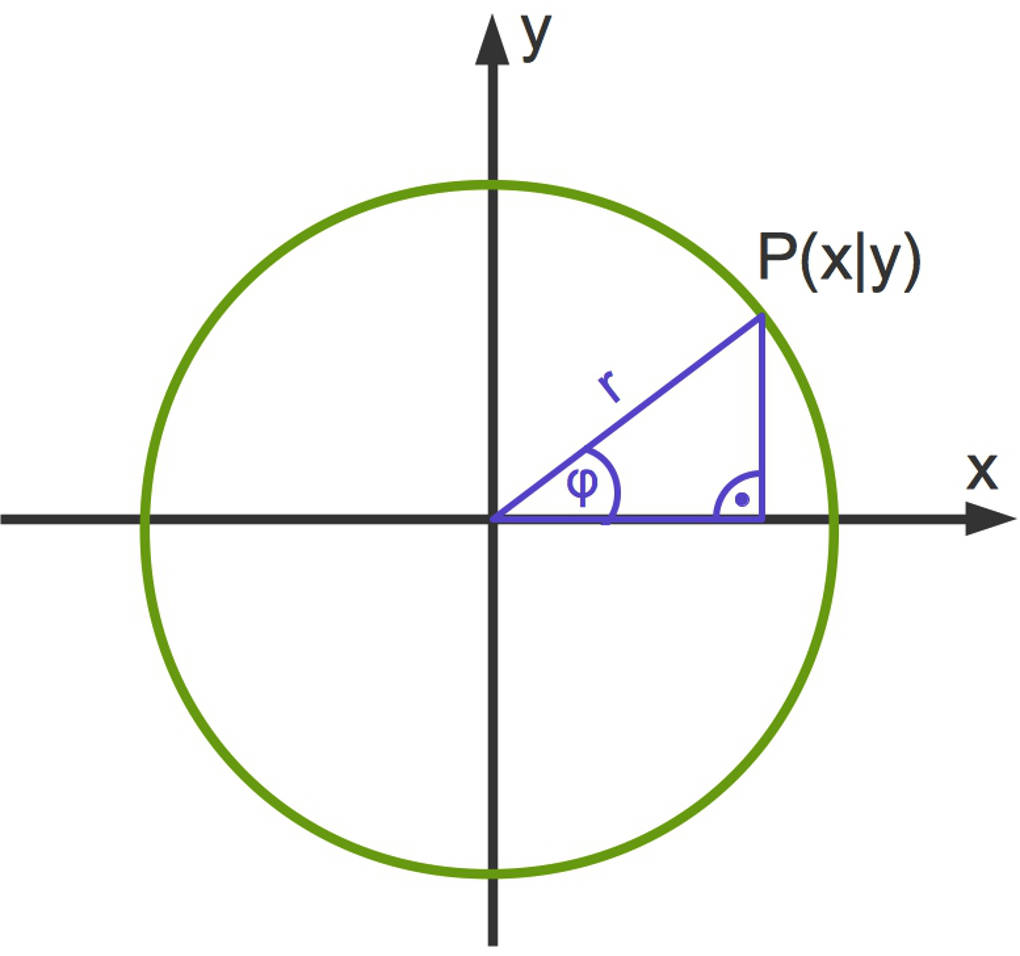
Es gilt
- $\cos(\varphi)=\frac xr$ oder, äquivalent dazu, $x=r\cdot \cos(\varphi)$.
- $\sin(\varphi)=\frac yr$ oder, äquivalent dazu, $y=r\cdot \sin(\varphi)$.
Dabei ist $r=\sqrt{x^2+y^2}$.
Das bedeutet, dass zu jedem Punkt eindeutig ein $r$ sowie ein Winkel $\varphi$ gehören. Du kannst dann den Punkt auch in Polarkoordinaten schreiben: $P(r|\varphi)$.
Beispiel 1
Hier siehst du, wie du von kartesischen Koordinaten in Polarkoordinaten umrechnen kannst.
Für den Punkt $P(4|3)$ ist
- $r=\sqrt{4^2+3^2}=\sqrt{25}=5$ und
- somit $\varphi=\cos^{-1}\left(\frac45\right)\approx36,9^\circ$.
Die Darstellung des Punktes in Polarkoordinaten lautet dann $P(5|36,9^\circ)$.
Beispiel 2
Umgekehrt kannst du auch Polarkoordinaten in kartesische Koordinaten umrechnen.
Für den Punkt $Q(\sqrt{8}|45^\circ)$ ist
- $x=\sqrt8\cdot \cos(45^\circ)=2$ sowie
- $y=\sqrt8\cdot \sin(45^\circ)=2$.
Die Darstellung des Punktes in kartesischen Koordinaten lautet dann $Q(2|2)$.
Alle Lerntexte zum Thema
Lerntexte zum Thema
Winkelfunktionen und Einheitskreis (2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Winkelfunktionen und Einheitskreis (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen




 Polarkoordinaten
Polarkoordinaten









