Schrägbilder von Würfel und Quader
Das Schrägbild eines Körpers ist eine dreidimensional wirkende Darstellung des Körpers auf einer ebenen Fläche.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Darstellung von Körpern im Schrägbild
- Verzerrungswinkel und Verkürzungsfaktoren
- Schrägbild eines Quaders konstruieren
Darstellung von Körpern im Schrägbild
Das Schrägbild eines Körpers ist eine dreidimensional wirkende Darstellung des Körpers auf einer ebenen Fläche, also zum Beispiel auf einem Blatt Papier.
Dabei bleibt die Vorderansicht unverändert. Die Seiten- und die Deckfläche werden hingegen verkürzt gezeichnet. Die Kanten des Körpers laufen schräg nach hinten in einem bestimmten Winkel $\alpha$ weg. Dieser Winkel wird auch als Verzerrungswinkel bezeichnet. Die schräg nach hinten laufenden Kanten sind auch kürzer als im Original. Parallele Kanten bleiben aber parallel.
Verzerrungswinkel und Verkürzungsfaktoren
Meistens zeichnet man Schrägbilder mit einem Winkel von $\alpha = 45^\circ$. Der zugehörige Verkürzungsfaktor $k$ für die Kanten beträgt dann $k = \frac{ 1 }{ 2 }$. Andere typische Werte sind:
- $\alpha = 30^\circ,~ k = \frac{ 2 }{ 3 }$
- $\alpha = 60^\circ,~ k = \frac{ 1 }{ 3 }$
Die folgende Abbildung zeigt drei Schrägbilder eines Würfels mit unterschiedlichen Verzerrungswinkeln.

Beträgt die Kantenlänge des Würfels beispielsweise $a = 6\ \text{cm}$, dann haben die schräg nach hinten laufenden Kanten die folgenden Längen:
- linkes Bild: $\frac{ 1 }{ 2 } \cdot 6\ \text{cm} = 3\ \text{cm}$
- mittleres Bild: $\frac{ 2 }{ 3 } \cdot 6\ \text{cm} = 4\ \text{cm}$
- rechtes Bild: $\frac{ 1 }{ 3 } \cdot 6\ \text{cm} = 2\ \text{cm}$
Schrägbild eines Quaders konstruieren
Im Folgenden wird gezeigt, wie du das Schrägbild eines Quader) konstruierst. Tipp: Zur leichteren Darstellung kannst du das Schrägbild auf kariertem Papier zeichnen.
Gesucht ist das Schrägbild eines Quaders mit den Seitenlängen $a = 4\ \text{cm}$, $b = 1\ \text{cm}$ und $c = 2\ \text{cm}$ sowie dem Verzerrungswinkel $\alpha = 45^\circ$ und dem Verkürzungsfaktor $k = \frac{ 1 }{ 2 }$.
- Zeichne die Vorderfläche (Ansicht) des Körpers in unveränderter Größe mit $a = 4\ \text{cm}$ und $b = 1\ \text{cm}$.
- Trage an der rechten unteren Ecke einen Winkel mit $45^\circ$ ab (oder zeichne eine Diagonale durch die quadratischen Karo-Kästchen) und zeichne die Länge $c = 2\ \text{cm}$ um den Faktor $\frac{ 1 }{ 2 }$ verkürzt, also $1\ \text{cm}$ lang.
- Von jedem Eckpunkt der Vorderansicht zeichnest du eine Parallele zur Grundkante mit der Länge $1\ \text{cm}$. Denk daran, die unsichtbare Kante gestrichelt darzustellen.
- Verbinde die Eckpunkte der schräg nach hinten verlaufenden Kanten mit Parallelen. Achte dabei auf die unsichtbaren Kanten, die gestrichelt gezeichnet werden.
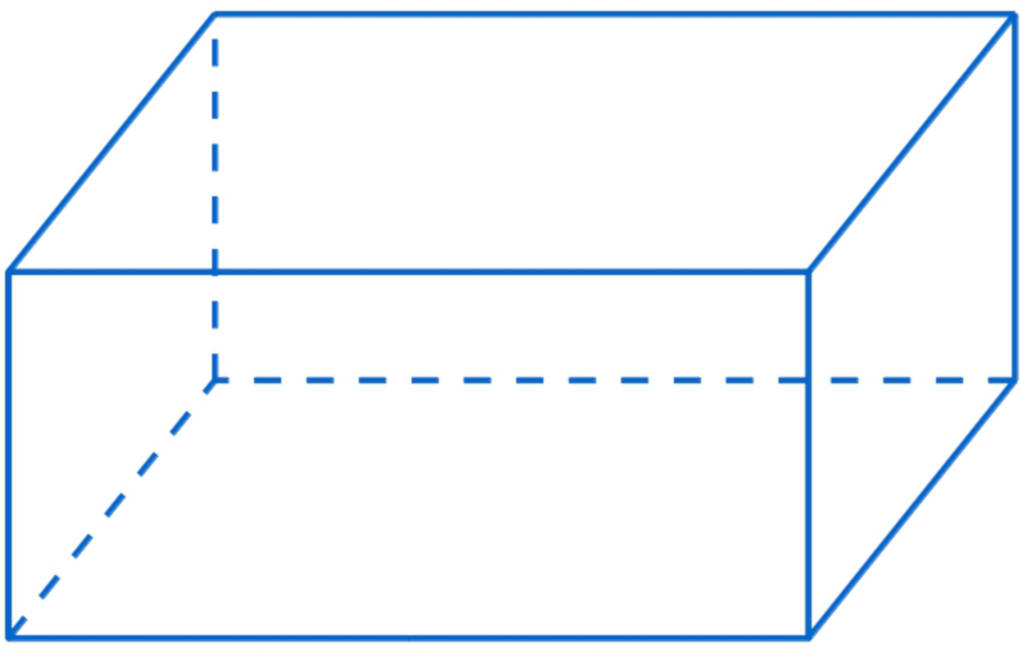
So kannst du das Schrägbild eines Quaders Zeichnen. Bei einem Würfel gehst du genauso vor.
Alle Videos zum Thema
Videos zum Thema
Schrägbilder von Würfel und Quader (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Schrägbilder von Würfel und Quader (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen






 Schrägbild des Würfels
Schrägbild des Würfels
 Schrägbild des Quaders
Schrägbild des Quaders









