Grundlagen zu Exponentialfunktionen
Exponentialfunktionen, ihre Eigenschaften und ihre Anwendung im Alltag
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine Exponentialfunktion?
- Eigenschaften von Exponentialfunktionen
- Beispiele für Exponentialfunktionen
- Definitions- und Wertebereich
- Monotonie und Verhalten
- Funktionsgleichung am Graphen bestimmen
Was ist eine Exponentialfunktion?
Um Funktionen zu klassifizieren, unterscheiden wir, ob sich die Variable $x$ in der Basis oder im Exponenten befindet. Bei Potenzfunktionen befindet sich die Variable in der Basis, wir schreiben folgende Funktionsgleichung:
$f(x) = x^{a}$
Dagegen befindet sich die Variable bei Exponentialfunktionen – wie der Name schon sagt – im Exponenten und die Funktionsgleichung hat dann folgende Form:
$f(x) = a^{x}$
Die Basis $a$ bleibt konstant, während für den Exponenten verschiedene Zahlen eingesetzt werden können. Es gilt:
$a\in\mathbb{R}^{+}\setminus\{1\}$
Die Basis $a$ ist also eine positive reelle Zahl außer $1$. Dies ist damit zu begründen, dass wir im Falle $a = 1$ mit $f(x) = 1^{x} = 1$ eine Parallele zur $x$-Achse, also eine konstante Funktion hätten.
Des Weiteren darf $a$ keinen negativen Wert annehmen, wenn wir beispielsweise folgende Darstellung für $a = -2$ und $x = \frac{3}{4}$ betrachten:
$\begin{array}{lll} f(\frac{3}{4})&=&(-2)^\frac{3}{4}\\ &=&\sqrt[4]{(-2)^3}\\ &=&\sqrt[4]{-8} \end{array}$
Wir bekommen für diesen Fall kein reelles Ergebnis, da sich aus negativen Zahlen nicht die vierte Wurzel ziehen lässt.
Eigenschaften von Exponentialfunktionen
Im Folgenden betrachten wir einige Beispiele und Eigenschaften von Exponentialfunktionen.
Beispiele für Exponentialfunktionen
In einer Exponentialfunktion finden wir immer eine positive Basis ungleich $1$ und einen Exponenten, der die Variable enthält. Deshalb können wir für die Basis $a$ ganze Zahlen, Brüche und irrationale Zahlen einsetzen, wie folgende Beispiele zeigen:
$f(x) = 2^{x} \\ f(x) = \frac{1}{2}^{x} \\ f(x) = \sqrt{17}^{x} \\ f(x) = 4\cdot 2^{x} \\ f(x) = 4\cdot 2^{3\cdot x - 0,1} - 23\cdot x$
Definitions- und Wertebereich
Betrachten wir die allgemeine Funktionsgleichung $f(x) = a^{x}$ mit $a \in\mathbb{R}^{+}\setminus {1}$, so erkennen wir, dass der Definitionsbereich die reellen Zahlen $\mathbb{R}$ und der Wertebereich die reellen Zahlen größer $0$, also $\mathbb{R}^+$ umfasst. Für $a=1,5$ kann man diese Eigenschaft dem folgenden Funktionsgraphen entnehmen:
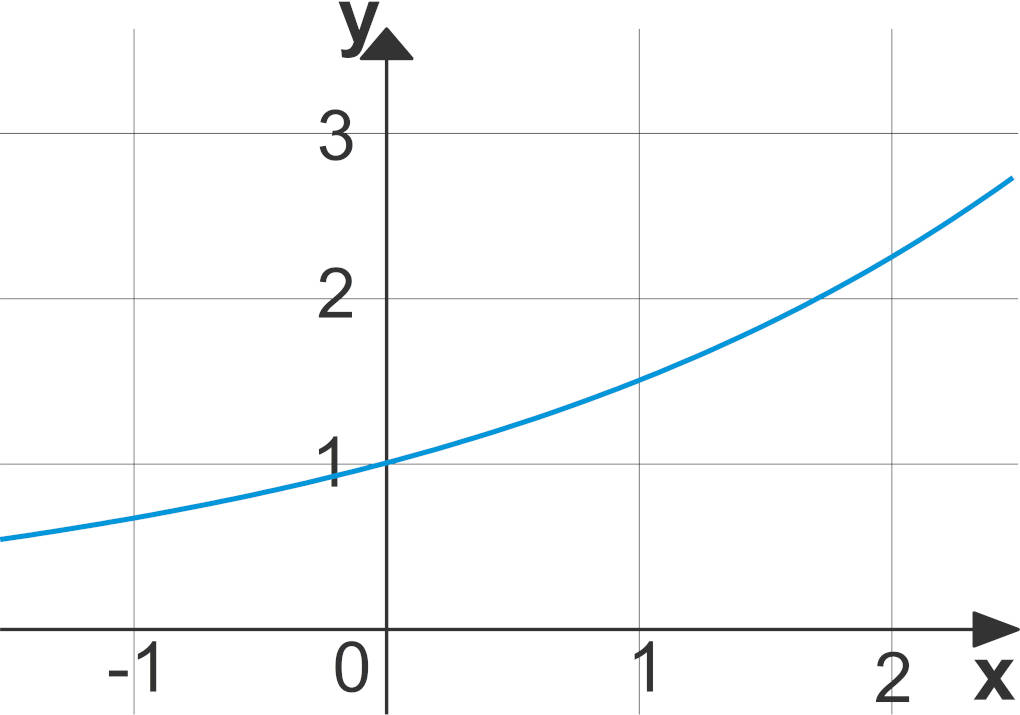
Monotonie und Verhalten
In der obigen Abbildung für $a=1,5$ erkennen wir, dass der Graph für $a\gt1$ streng monoton steigt. Es gilt nämlich:
$x_1 \lt x_2 ~ \rightarrow ~ a^{x_1}\lt a^{x_2}$
Für positive $x$-Werte streben die Funktionswerte gegen $\infty$, für negative $x$-Werte streben die Funktionswerte gegen $0$.
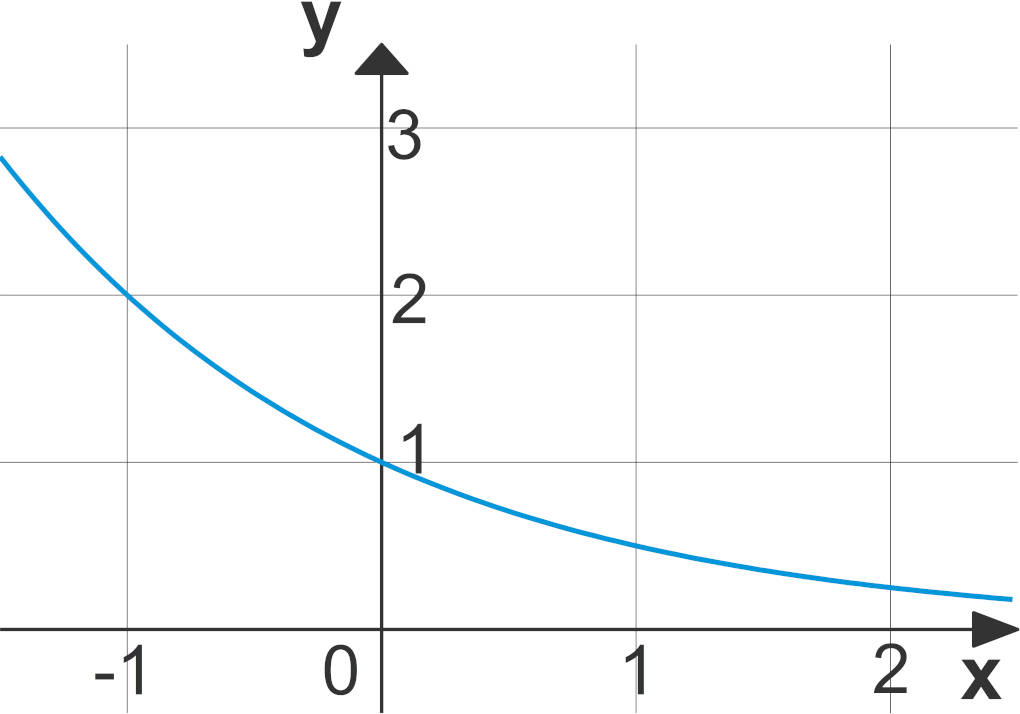
Betrachten wir nun den Fall $0\lt a\lt 1$, so ist der Graph streng monoton fallend. Diese Eigenschaft können wir dem obigen Graphen für $a=0,5$ ebenfalls entnehmen. Es gilt nämlich:
$x_1 \lt x_2 ~ \rightarrow ~ a^{x_1}\gt a^{x_2}$
Für positive $x$-Werte streben die Funktionswerte gegen $0$, für negative $x$-Werte streben die Funktionswerte gegen $\infty$.
Funktionsgleichung am Graphen bestimmen
Wir können für die allgemeine Exponentialfunktion $f(x) = b\cdot a^{x}$ eine nützliche Eigenschaft hinzuziehen. Es gibt immer zwei Punkte, die Elemente des Graphen sind:
- Der Punkt $(0|b)$ folgt aus $f(0) = b\cdot a^{0} = b\cdot 1 = b$. In diesem Punkt schneidet der Graph die $y-$Achse.
- Der Punkt $(1|ab)$ folgt aus $f(1) = b\cdot a^{1} = b\cdot a = ab$.
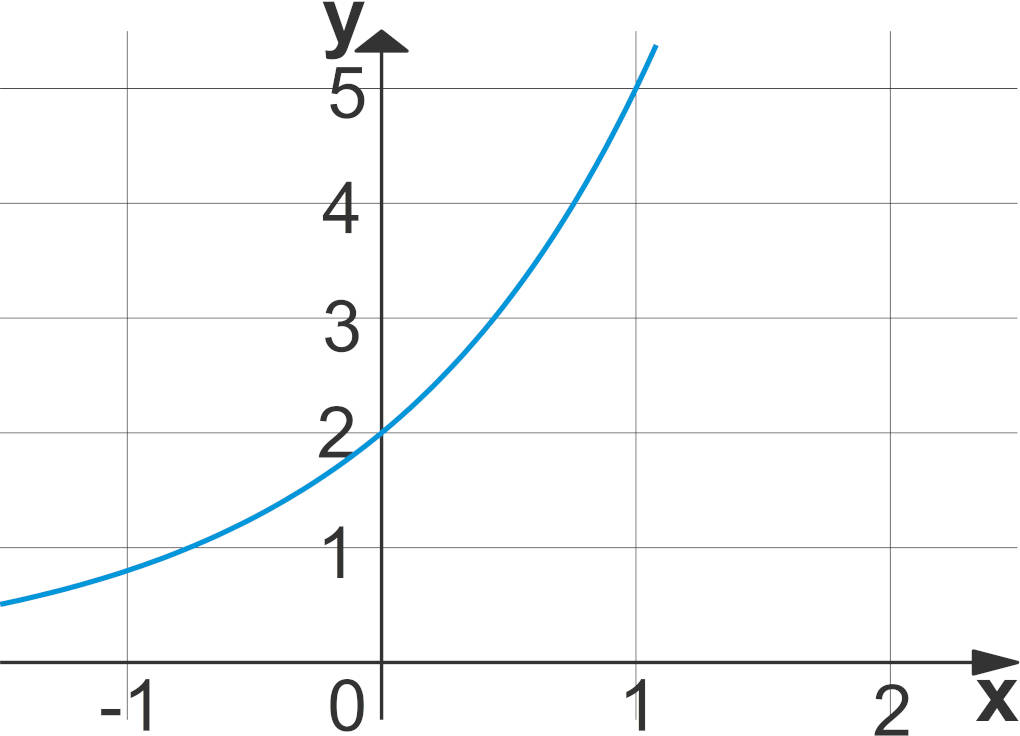
Aus dem obigen Graphen entnehmen wir den $y$-Achsenschnittpunkt $S_y(0\vert 2)$. Es gilt also $b = 2$ und somit folgt aus dem Punkt $(1\vert ab)$:
$\begin{array}{llll} f(1) &=& 5 & \\ b\cdot a^1 &=& 5 & \vert b=2\ \text{einsetzen} \\ 2\cdot a &=& 5 & \vert :2 \\ a &=& 2,5 & \end{array}$
Daraus folgt schließlich $a = 2,5$ und wir erhalten für den abgebildeten Graphen folgende Funktionsgleichung:
$f(x) = 2\cdot 2,5^{x}$
Anwendungsbeispiele
Exponentialfunktionen spielen in der Mathematik eine sehr wichtige Rolle, um Wachstums- und Zerfallsprozesse darzustellen. Sie lassen sich in folgender Form schreiben:
$f(x) = b\cdot a^{x}$
Zunächst beschäftigen wir uns mit dem Wachstumsprozess einer Bakterienkultur, die anfangs aus $100$ Bakterien besteht und sich stündlich verdoppelt.
$\begin{array}{lllllll} t = 0 && 1000 &=& 1000\cdot 1 &=& 1000\cdot 2^0 \\ t = 1 && 2000 &=& 1000\cdot 2 &=& 1000\cdot 2^1 \\ t = 2 && 4000 &=& 1000\cdot 2\cdot 2 &=& 1000\cdot 2^{2} \\ t = 3 && 8000 &=& 1000\cdot 2\cdot 2\cdot 2 &=& 1000\cdot 2^{3} \end{array}$
Zum Zeitpunkt $t$ erhalten wir dann:
$N = 1000\cdot \underbrace{2\cdot 2\cdot …\cdot 2}_{t\text{-mal}} = 1000\cdot 2^{t}$
So kann der Wachstumsprozess dieser Bakterienkultur mithilfe folgender Exponentialfunktion beschrieben werden:
$N(t) = 1000\cdot 2^{t}$
Unter $N(t)$ verstehen wir die Anzahl der Bakterien zum Zeitpunkt $t$.
Das nachfolgende Beispiel zeigt uns, wie wir eine Exponentialfunktion für radioaktiven Zerfall aufstellen, wenn sich die anfangs $1000$ Teilchen stündlich halbieren:
$\begin{array}{llrll} t = 0 && 1000 &=& 1000\cdot \left(\frac{1}{2}\right)^{0} \\ t = 1 && 500 &=& 1000\cdot \left(\frac{1}{2}\right)^{1} \\ t = 2 && 250 &=& 1000\cdot \left(\frac{1}{2}\right)^{2} \\ t = 3 && 125 &=& 1000\cdot \left(\frac{1}{2}\right)^{3} \\ t = t && N &=& 1000\cdot \left(\frac{1}{2}\right)^{t} \end{array}$
Für den beschriebenen Zerfallsprozess können wir die Anzahl der Teilchen zum Zeitpunkt $t$ ermitteln:
$N(t)= 1000\cdot \left(\frac{1}{2}\right)^{t}$
In diesem Zusammenhang wird auch häufig mit der Halbwertszeit gerechnet. Damit ist die Zeit gemeint, die vergeht, bis sich die Menge eines Stoffes halbiert hat.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Grundlagen zu Exponentialfunktionen (2 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grundlagen zu Exponentialfunktionen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter








 Exponentialfunktion – Definition
Exponentialfunktion – Definition
 Parameter der Exponentialfunktion
Parameter der Exponentialfunktion
 Exponentialfunktionen – Anwendungen
Exponentialfunktionen – Anwendungen









