Parabelscharen

Inhaltsverzeichnis zum Thema

• Was ist eine quadratische Funktion?
• Veränderung des Parameters $a$
• Veränderung des Parameters $c$
• Veränderung des Parameters $b$ – Ortskurven
• Bestimmen des tiefsten Punktes
• Herleitung der Ortskurve

Was ist eine quadratische Funktion?

Eine quadratische Funktionsgleichung hat die Form $f(x)=ax^2+bx+c$. Dabei hängt der Funktionsgraph der quadratischen Funktion von den Parametern $a$, $b$ und $c$ ab. Übrigens: Der Funktionsgraph einer quadratischen Funktion ist eine Parabel.

Wenn eine Funktion $f$ zusätzlich zu der Variablen $x$ auch noch einen Parameter hat, so spricht man von einer Funktionenschar. Die zugehörigen Funktionsgraphen werden schließlich als Parabelschar bezeichnet.

Veränderung des Parameters $a$

Wenn du zum Beispiel die Funktionenschar $f_{a}$ mit $f_{a}(x)=$ $ax^{2}$ betrachtest, erkennst du, dass alle Parabeln den gemeinsamen Scheitelpunkt $O(0|0)$, den Koordinatenursprung, haben. Sie unterscheiden sich zum einen dadurch, dass sie nach oben oder unten geöffnet sind, und zum anderen dadurch, wie weit sie geöffnet sind.

Hier siehst du Parabeln zu verschiedenen Werten für den Parameter $a$, welcher auch als Streckfaktor bezeichnet wird. Die gelbe Parabel ist die Normalparabel zu der Funktion $f$ mit $f(x)=x^{2}$.

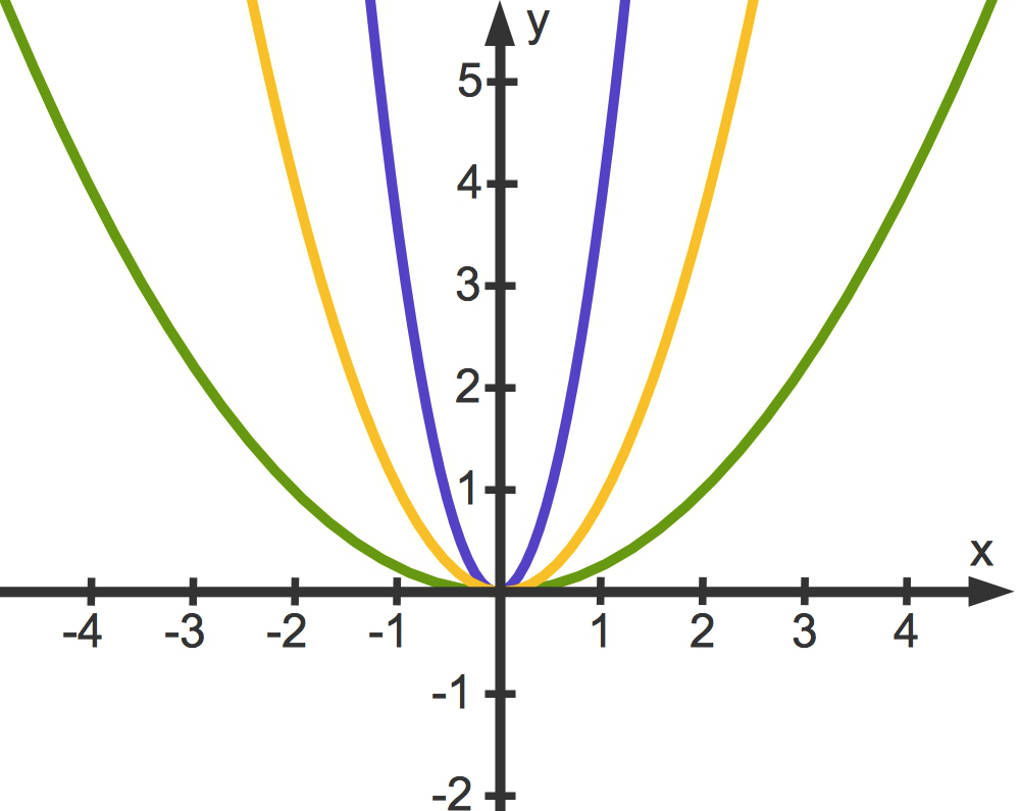
• Die blaue Parabel ist gestreckt. Sie gehört zu der Funktionsgleichung $h(x)=4x^{2}$.
• Die grüne Parabel ist gestaucht. Sie gehört zu der Funktionsgleichung $k(x)=\frac12x^{2}$.

Veränderung des Parameters $c$

Hierfür schauen wir uns die Funktionenschar $f_{c}$ mit $f_{c}(x)=x^{2}+c$ an. Wenn du $c$ veränderst, wird die Parabel entlang der $y$-Achse verschoben. Die Parabel wird nach oben verschoben, wenn $c\gt 0$ ist und für $c\lt 0$ nach unten.

Hier siehst du Parabeln zu verschiedenen Werten für den Parameter $c$. Wieder ist die gelbe Parabel die Normalparabel zu $f(x)=x^{2}$.

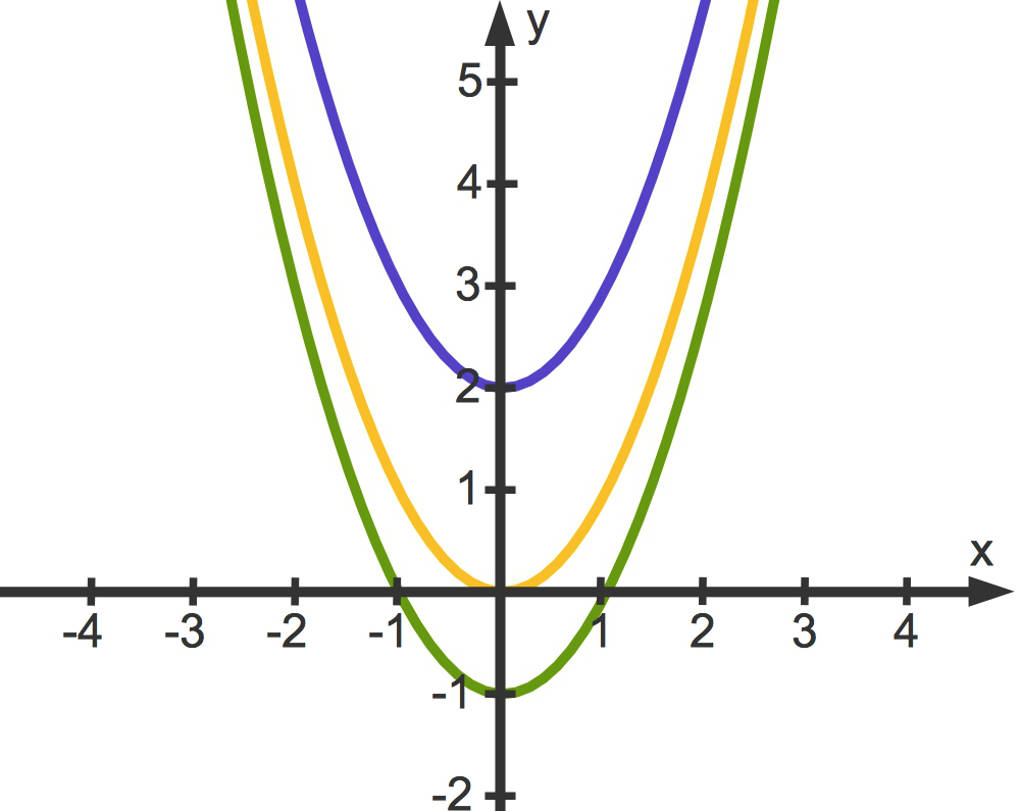
• Die blaue Parabel ist nach oben verschoben. Sie gehört zu der Funktionsgleichung $h(x)=x^{2}+2$.
• Die grüne Parabel ist nach unten verschoben. Sie gehört zu der Funktionsgleichung $k(x)=x^{2}-1$.

Veränderung des Parameters $b$ – Ortskurven

Schau dir die Funktionenschar $f_b$ mit $f_{b}(x)=x^2+2bx+2$ an. Wir möchten untersuchen, wie die Scheitelpunkte der Parabeln von dem Parameter $b$ abhängen. Da in diesem Beispiel der Streckfaktor $a=1$ positiv ist, sind die zugehörigen Parabeln der Parabelschar alle nach oben geöffnet. Der Scheitelpunkt ist also der jeweils tiefste Punkt der Parabel.

Bestimmen des tiefsten Punktes

Wie bestimmst du den tiefsten Punkt, also das Minimum, einer Funktion? Richtig, du benötigst die ersten beiden Ableitungen $f'_{b}(x)$ sowie $f''_{b}(x)$ der Funktion. Dann löst du die Gleichung $f'_{b}(x)=0$. Die zweite Ableitung ist in diesem Fall immer größer als $0$.

Los geht’s:

• $f'_{b}(x)=2x+2b$,
• $f''_{b}(x)=2\gt 0$.

Löse nun die Gleichung $f'_{b}(x)=0$, also $2x+2b=0$.

$\begin{array}{rclll} 2x+2b&=&0&|&-2b\\ 2x&=&-2b&|&:2\\ x&=&-b \end{array}$

Berechne nun die $y$-Koordinate des Scheitelpunktes $y=f_{b}(-b)=(-b)^2+2b(-b)+2=-b^{2}+2$.

Der Scheitelpunkt $S\left(-b|-b^{2}+2\right)$ hängt also sowohl in der $x$- als auch in der $y$-Koordinate von dem Parameter $b$ ab.

Im Folgenden siehst du drei Parabeln:

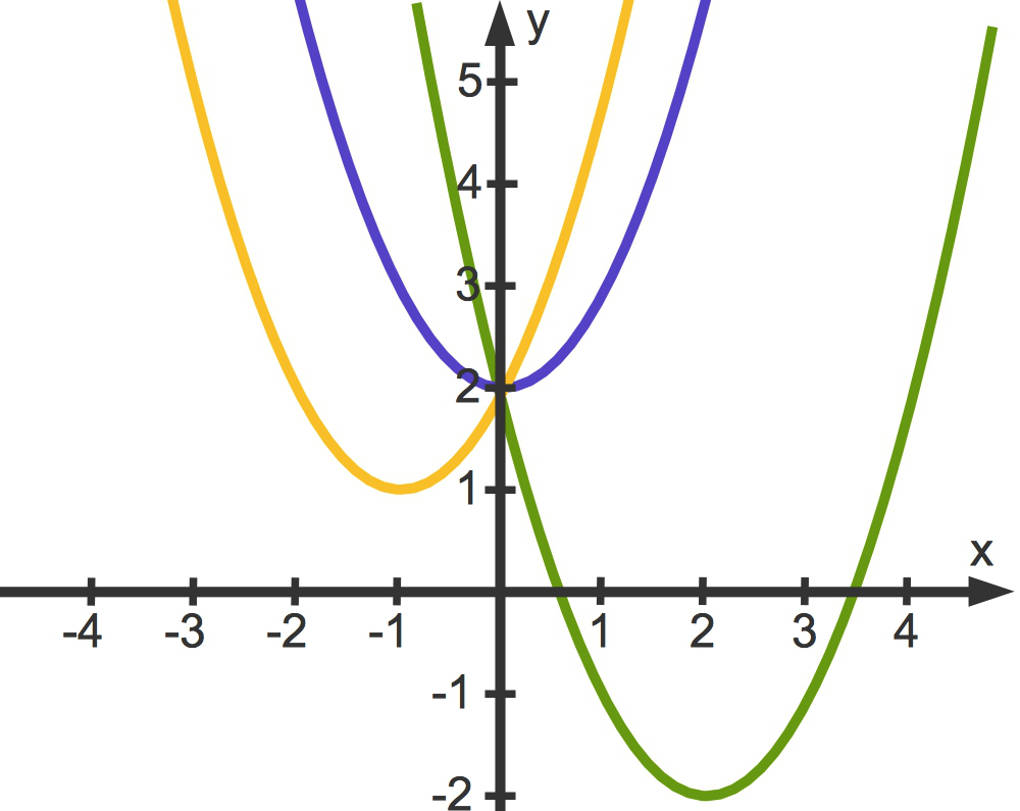
• $b=0$: Die blaue Parabel hat den Scheitelpunkt $S(0|2)$.
• $b=1$: Die gelbe Parabel hat den Scheitelpunkt $S(-1|1)$.
• $b=-2$: Die grüne Parabel hat den Scheitelpunkt $S(2|-2)$.

Jeden dieser Scheitelpunkte erhältst du durch Einsetzen des jeweiligen Wertes für $b$ in den oben berechneten Scheitelpunkt.

Herleitung der Ortskurve

Was ist eigentlich eine Ortskurve? Auf einer Ortskurve liegen alle Punkte einer Funktionenschar, die eine gemeinsame Eigenschaft haben. In diesem Beispiel sind dies die Scheitelpunkte, also Minima, der Funktionenschar.

Wie kannst du eine solche Ortskurve bestimmen? Du gehst so vor:

1. Forme die $x$-Koordinate des Scheitelpunktes nach dem Parameter um. Wenn du die Gleichung $x=-b$ mit $-1$ multiplizierst, erhältst du $b=-x$.
2. Setze den so gefundenen Parameter in die $y$-Koordinate ein: $y=y(x)=-(-x)^{2}+2=-x^2+2$.

Du hast die Funktionsgleichung der Ortskurve gefunden. Es handelt sich um eine nach unten geöffnete Normalparabel, welche um $2$ Einheiten nach oben verschoben ist:

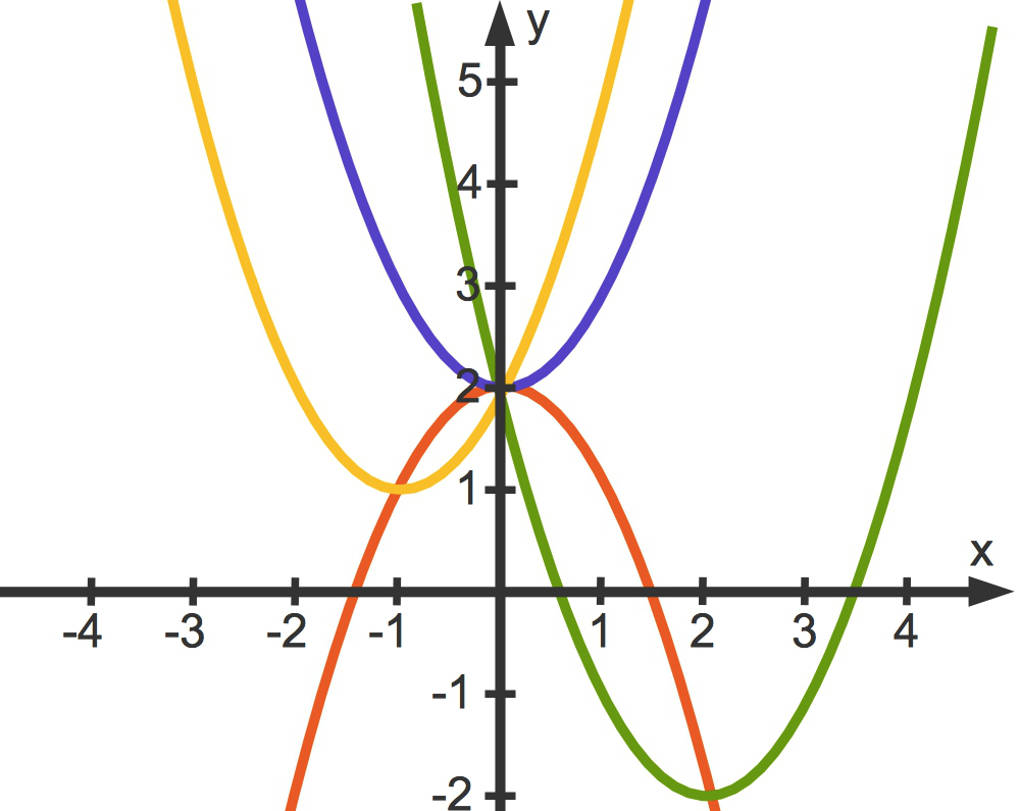
Du kannst erkennen, dass auf der rot eingezeichneten Parabel, der Ortskurve, die Scheitelpunkte der drei dargestellten Parabeln liegen.