Grenzwertsätze

Inhaltsverzeichnis zum Thema

• Was ist der Grenzwert einer Funktion?
• Beispiele für Grenzwerte
• Der Grenzwert einer Summenfunktion
• Beispiel 1
• Beispiel 2
• Der Grenzwert einer Differenzfunktion
• Beispiel
• Der Grenzwert einer Produktfunktion
• Beispiel 1
• Beispiel 2
• Der Grenzwert einer Quotientenfunktion
• Beispiel

Was ist der Grenzwert einer Funktion?

Am Ende einer Kurvendiskussion kannst den Funktionsgraphen einer Funktion zeichnen oder, genauer, einen Ausschnitt dieses Funktionsgraphen.

Du kannst dich dann noch fragen, wie sich die Funktion außerhalb dieses Ausschnittes verhält. Welche Funktionswerte werden angenommen, wenn $x$ immer größer oder immer kleiner wird?

Wenn eine Polstelle, also eine Definitionslücke vorliegt, kannst du auch untersuchen, wie die Funktion sich an dieser Polstelle verhält.

Mathematisch drückt man dies so aus:

• $\lim\limits_{x\to \infty}~f(x)=?$,
• $\lim\limits_{x\to -\infty}~f(x)=?$ oder
• $\lim\limits_{x\to x_0}~f(x)=?$.

Es wird also nach dem Verhalten im Unendlichen oder dem Verhalten an einer festen Stelle $x_0$ gefragt, dem Grenzwert.

Dabei steht

• „$\lim$“ für „Limes“, lateinisch für „Grenze“ und
• unter „$\lim$“, wogegen $x$ gehen soll.

Beispiele für Grenzwerte

Die Funktion $f(x)=\frac1x$, mit dem Definitionsbereich $\mathbb{D}_f=\mathbb{R}\setminus\{0\}$, hat die Grenzwerte

$\lim\limits_{x\to \infty}~f(x)=\lim\limits_{x\to -\infty}~f(x)=0$.

Übrigens: Wenn $x$ gegen $0$ geht, gilt

• $\lim\limits_{x\to 0;~x>0}~f(x)=$„$\infty$“ sowie
• $\lim\limits_{x\to 0;~x<0}~f(x)=$„$-\infty$“.

Den Funktionsgraphen kannst du hier sehen.

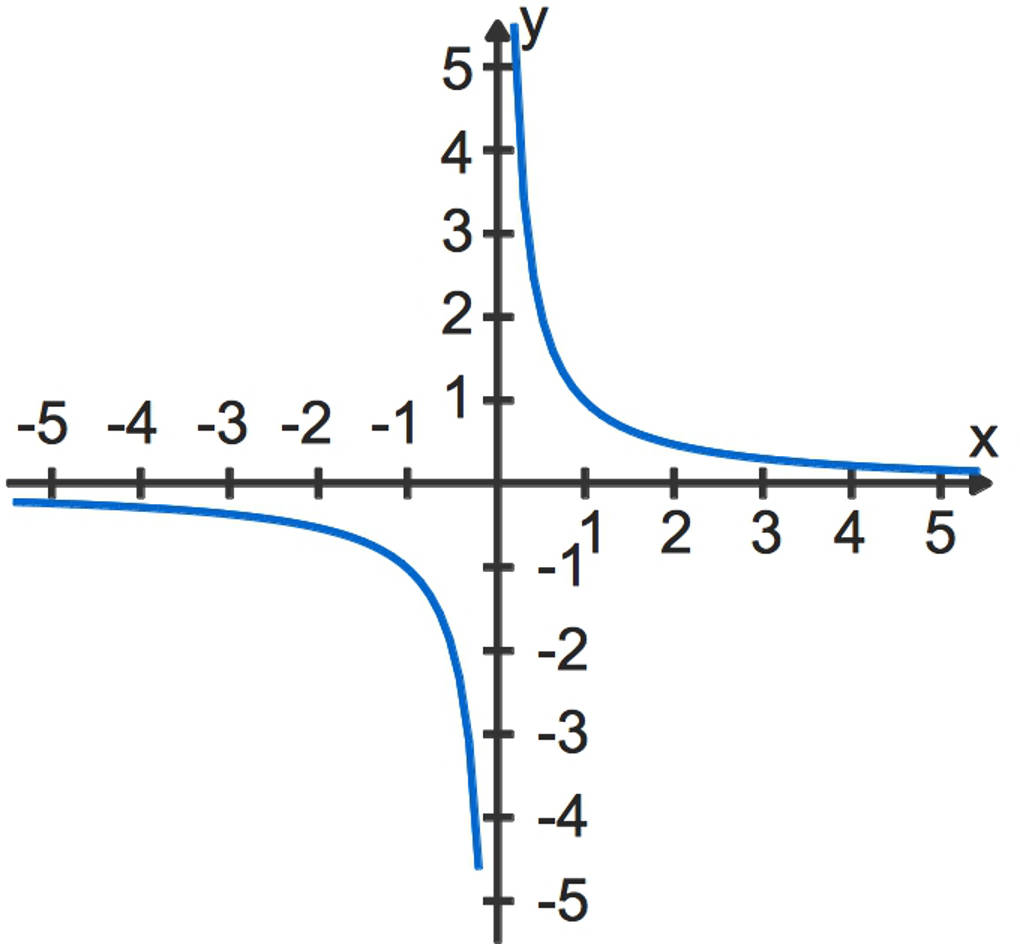
Die Funktion $g(x)=5$, eine konstante Funktion, hat die Grenzwerte

$\lim\limits_{x\to \infty}~f(x)=\lim\limits_{x\to -\infty}~f(x)=5$.

Für jede konstante Funktion gilt, dass der Grenzwert sowohl für $x\to\infty$ als auch für $x\to-\infty$ gerade der konstante Funktionswert ist.

Nun schauen wir uns die Grenzwertsätze für Funktionen an. Dabei betrachten wir die vier Grundrechenarten:

• die Addition: Summand plus Summand gleich Summe,
• die Subtraktion: Minuend minus Subtrahend gleich Differenz,
• die Multiplikation: Faktor mal Faktor gleich Produkt und
• die Division: Dividend durch Divisor gleich Quotient.

Der Grenzwert einer Summenfunktion

Wenn du den Grenzwert einer Summenfunktion berechnen möchtest, kannst du die Grenzwerte der einzelnen Summanden berechnen und diese addieren:

$\lim\limits_{x\to\infty}(f(x)+ g(x))=\lim\limits_{x\to\infty}f(x)+\lim\limits_{x\to\infty}g(x)$.

Beispiel 1

Hierfür schauen wir uns das folgende Beispiel an: $f(x)=\frac1x+5$.

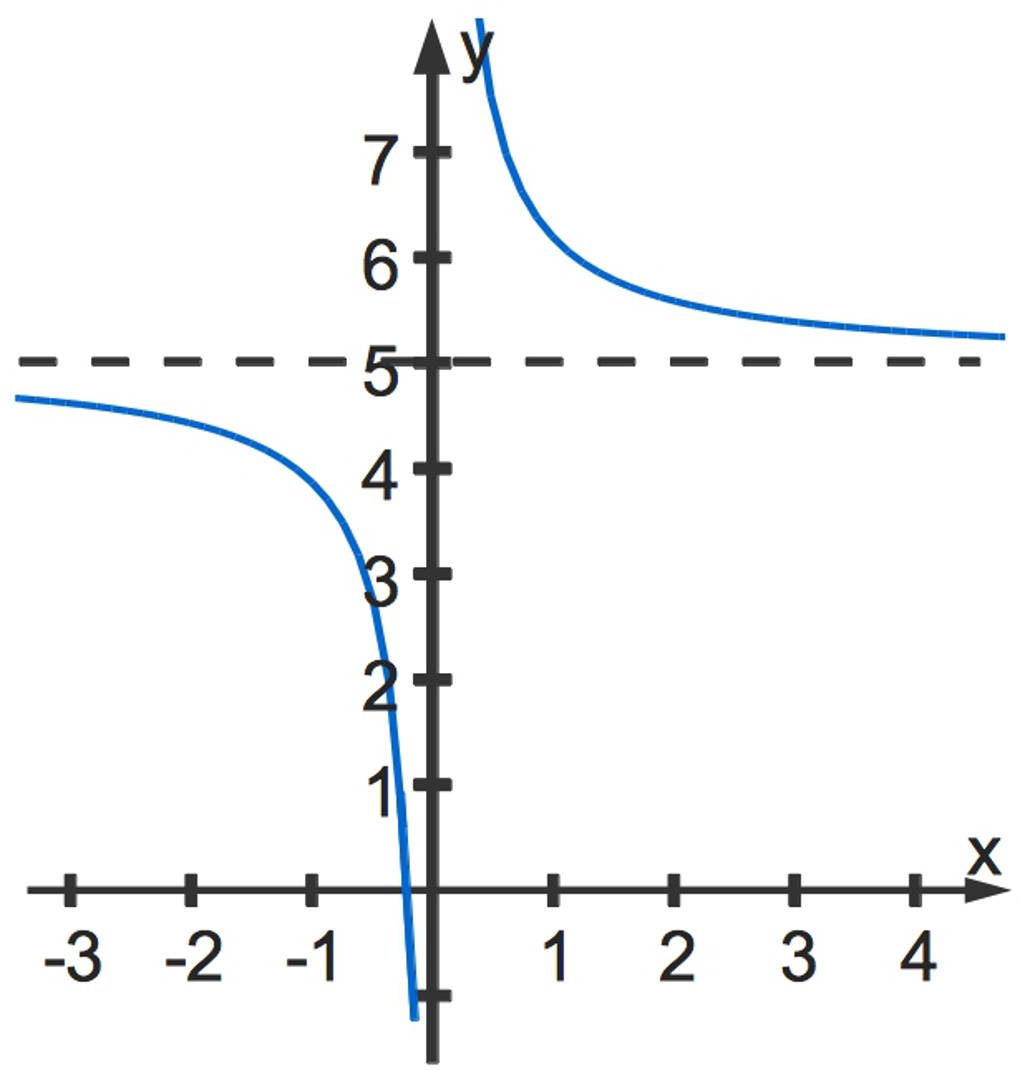
Damit ist

$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}\left(\frac1x+ 5\right)=\lim\limits_{x\to\infty}\frac1x+\lim\limits_{x\to\infty}5=0+5=5$.

Beispiel 2

Du kannst mit diesem Grenzwertsatz auch zeigen, dass zum Beispiel $g(x)=\frac2x$ den folgenden Grenzwert hat:

$\lim\limits_{x\to\infty}g(x)=\lim\limits_{x\to\infty}\left(\frac1x+ \frac1x\right)=\lim\limits_{x\to\infty}\frac1x+\lim\limits_{x\to\infty}\frac1x=0+0=0$.

Allgemein gilt, dass

$\lim\limits_{x\to\infty}\left(\frac ax\right) =0$

ist für eine beliebige reelle Zahl $a$.

Der Grenzwert einer Differenzfunktion

Der Grenzwert einer Differenzfunktion ist die Differenz der Grenzwerte des Minuenden und des Subtrahenden:

$\lim\limits_{x\to\infty}(f(x)- g(x))=\lim\limits_{x\to\infty}f(x)-\lim\limits_{x\to\infty}g(x)$.

Beispiel

Hier schauen wir uns $f(x)=\frac{x-3}{x}$ an.

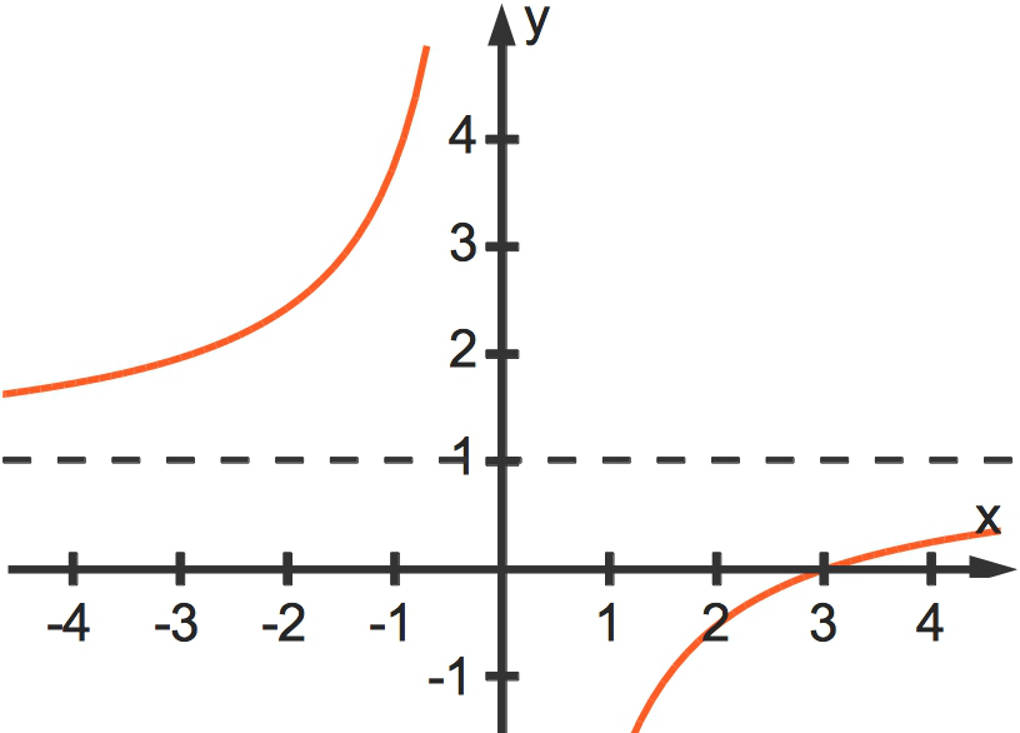
Zunächst einmal sind die Grenzwertsätze nicht anwendbar, da weder der Zähler noch der Nenner gegen eine endliche Zahl konvergieren. Wir formen die Funktion um zu $f(x)=1-\frac3x$. Jetzt kann der Grenzwertsatz für Differenzfunktionen angewendet werden:

$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}\left(1- \frac3x\right)=\lim\limits_{x\to\infty}1-\lim\limits_{x\to\infty}\frac3x=1-0=1$.

Der Grenzwert einer Produktfunktion

Bei einer Produktfunktion betrachtest du jeden einzelnen Faktor:

$\lim\limits_{x\to\infty}(f(x)\cdot g(x))=\lim\limits_{x\to\infty}f(x)\cdot \lim\limits_{x\to\infty}g(x)$.

Beispiel 1

Zunächst kann mit diesem Grenzwertsatz nachgewiesen werden, dass jede Funktion der Form $f(x)=\frac1{x^n}$, $n\ge 1$, gegen $0$ geht. Dies kannst du hier am Beispiel $n=2$ sehen:

$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}\left(\frac1x\cdot \frac1x\right)=\lim\limits_{x\to\infty}\frac1x\cdot \lim\limits_{x\to\infty}\frac1x=0\cdot 0=0$.

Beispiel 2

In dem folgenden Beispiel werden auch noch die ersten beiden Grenzwertsätze für Summen- und Differenzfunktionen verwendet: $f(x)=\frac{5+3x^2}{x^2}\cdot \frac{3x-2}{x}$.

Wir schauen uns hier jeden der beiden Faktoren an:

$\lim\limits_{x\to\infty}\frac{5+3x^2}{x^2}=\lim\limits_{x\to\infty}\left(\frac5{x^2}+3\right)= \lim\limits_{x\to\infty}\frac5{x^2}+ \lim\limits_{x\to\infty}3=0+3=3$ und

$\lim\limits_{x\to\infty}\frac{3x-2}{x}=\lim\limits_{x\to\infty}\left(3-\frac2x\right)= \lim\limits_{x\to\infty}3- \lim\limits_{x\to\infty}\frac2x=3+0=3$.

Also ist $\lim\limits_{x\to\infty}f(x)=3\cdot 3=9$.

Der Grenzwert einer Quotientenfunktion

Bei Quotientenfunktionen musst du beachten, dass weder der Divisor noch der Grenzwert des Divisors $0$ sein dürfen:

$\lim\limits_{x\to\infty}\left(\frac{f(x)}{g(x)}\right)=\frac{\lim\limits_{x\to\infty}f(x)}{\lim\limits_{x\to\infty}g(x)}$.

Dabei muss

• sowohl $g(x)\neq 0$
• als auch $\lim\limits_{x\to\infty}g(x)\neq 0$ sein.

Beispiel

Es soll die gebrochenrationale Funktion

$f(x)=\frac{3x^2-2x+4}{-4x^2+20x-123}$

untersucht werden. Sowohl der Term im Zähler als auch der Term im Nenner nimmt für immer größere $x$ immer größere Werte an.

Nun kannst du ja nicht $\infty$ durch $-\infty$ dividieren. Hier helfen dir die Grenzwertsätze weiter.

• Du klammerst sowohl im Zähler als auch im Nenner $x^2$ aus:

$f(x)=\frac{x^2\left(3-\frac2x+\frac4{x^2}\right)}{x^2\left(-4+\frac{20}x-\frac{123}{x^2}\right)}$.

• Nun kannst du den Faktor $x^2$ kürzen:

$f(x)=\frac{3-\frac2x+\frac4{x^2}}{-4+\frac{20}x-\frac{123}{x^2}}$.

• Zuletzt kannst du den Grenzwertsatz für Quotientenfunktionen anwenden:

$\begin{array}{rcl} \lim\limits_{x\to\infty}f(x)&=&\lim\limits_{x\to\infty}\frac{3-\frac2x+\frac4{x^2}}{-4+\frac{20}x-\frac{123}{x^2}}\\ &=&\frac{\lim\limits_{x\to\infty}\left(3-\frac2x+\frac4{x^2}\right)}{\lim\limits_{x\to\infty}\left(-4+\frac{20}x-\frac{123}{x^2}\right)}\\ &=&\frac{\lim\limits_{x\to\infty}3-\lim\limits_{x\to\infty}\frac2x+\lim\limits_{x\to\infty}\frac4{x^2}}{\lim\limits_{x\to\infty}(-4)+\lim\limits_{x\to\infty}\frac{20}x-\lim\limits_{x\to\infty}\frac{123}{x^2}}\\ &=&\frac{3-0+0}{-4+0-0}\\ &=&-\frac34 \end{array}$

In diesem Beispiel kommen alle Grenzwertsätze vor, die du gelernt hast.

Viel Spaß beim Üben.