Beschränktes Wachstum und beschränkter Zerfall

Inhaltsverzeichnis zum Thema

• Einleitung
• Beschränktes Wachstum
• Beschränkter Zerfall

Einleitung

Oft wird bei Wachstums- oder Zerfallsprozessen davon ausgegangen, dass es keine Schranke gibt. Zum Beispiel vermehren sich Bakterien in einem gegebenen Zeitraum immer um den gleichen Faktor. Wenn wir einmal davon ausgehen, dass unendlich viele Bakterien unendlich lange leben, was natürlich nicht stimmt, haben wir hier ein Beispiel für unbeschränktes Wachstum.

Ein solches Wachstum kann durch $N(t)=N_{0}\cdot e^{k\cdot t}$ dargestellt werden.

Dabei steht $N(t)$ für den Bestand zum Zeitpunkt $t$. Der Anfangsbestand, also zum Zeitpunkt $t=0$ ist $N_{0}$. Der Faktor $k$ ist ein Wachstumsfaktor.

In der Realität wird Wachstum meist nicht ohne Schranke möglich sein. Schaue dir die folgenden Beispiele an:

• Eine Seerosenkultur auf einem See wird immer größer. Da maximal die gesamte Oberfläche des Sees bedeckt werden kann, gibt es eine Grenze.
• Eine Neuigkeit verbreitet sich unter einer gewissen Anzahl von Menschen. Irgendwann kennen alle Menschen diese Neuigkeit. Die Anzahl der Menschen ist hier die obere Grenze.
• Bei einem Zerfall gibt es eine untere Grenze: Wenn du einen Tee kochst, ist er am Anfang sehr heiß. Der Tee kühlt ab. Die Abkühlung hängt von verschiedenen Parametern ab, zum Beispiel von der Beschaffenheit der Tasse. Wie auch immer: Der Tee wird sicher nie kälter als die Umgebungstemperatur. Dies ist die untere Grenze.

Wir schauen uns nun im Folgenden das beschränkte Wachstum sowie den beschränkten Zerfall an.

Beschränktes Wachstum

Dies schauen wir uns am Beispiel eines Handyanbieters an: Die Firma SmartCall hat ein innovatives neues Handy produziert. Die Firma beabsichtigt $100 000$ Handys zu verkaufen. Im ersten Quartal werden $50\%$ verkauft, von den verbleibenden im nächsten Quartal wieder $50\%$ und so weiter. Hier siehst du in Form einer Tabelle die Anzahl der verkauften Handys in Abhängigkeit von der Zahl der Quartale:

$\begin{array}{c|c|c|c|c|c|c} \text{Quartal}&1&2&3&4&5&6\\ \hline \text{Anzahl}&50000&75000&87500&93750&96875&98438 \end{array}$

Du kannst diesen Zusammenhang in einem Koordinatensystem darstellen.

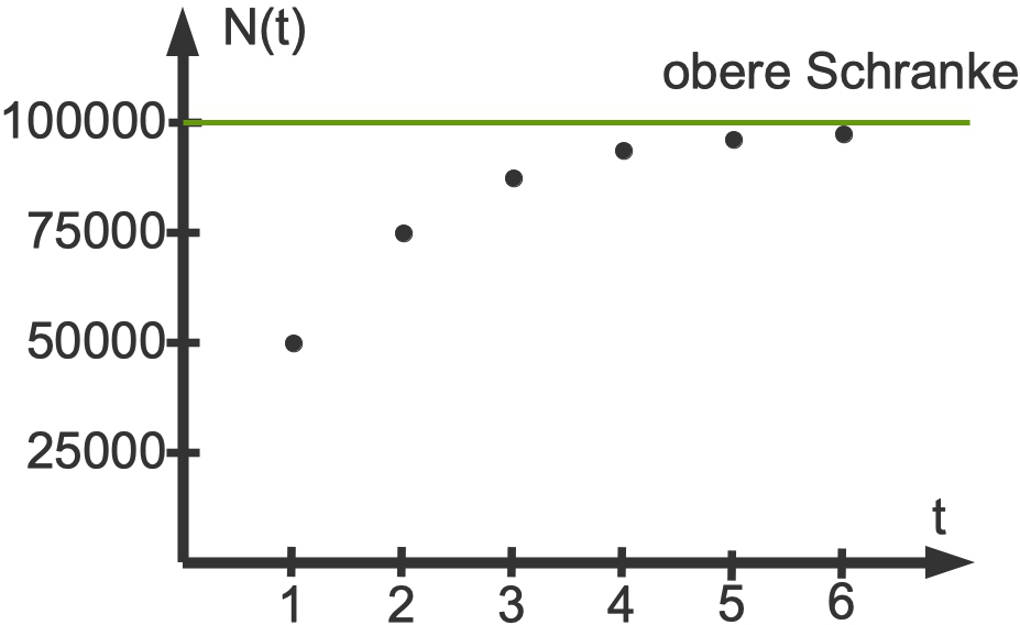
Du erkennst ein Wachstum sowie eine obere Schranke $G$, welche durch die Gesamtzahl der Handys, also $G=100 000$, gegeben ist.

Du kannst die dargestellte Entwicklung rekursiv beschreiben: $N(t+1)=N(t)+0,5\cdot (G-N(t))$. Der Faktor $0,5$ in diesem Beispiel entspricht den angegebenen $50\%$.

Allgemein ist $N(t+1)=N(t)+k\cdot (G-N(t))$.

Verwendest du nun die Differenz $N(t+1)-N(t)$ als Änderungsrate, erhältst du eine solche Differentialgleichung für das beschränkte Wachstum: $N'(t)=k\cdot (G-N(t))$. Dies ist eine lineare inhomogene Differentialgleichung. Die Lösung dieser Differentialgleichung ist gegeben durch die Funktion $N$:

$N(t)=G-(G-N_0)\cdot e^{-kt};~k\gt 0$

Dabei ist $N_{0}$ der Anfangsbestand. Dies ist die explizite Darstellung eines beschränkten Wachstums.

Beschränkter Zerfall

Dies schauen wir uns am Beispiel einer leckeren Tasse Tee an:

Zu Beginn hat der Tee eine Temperatur von $70^{\circ}$. Der Tee wird nach und nach abkühlen, allerdings kann er nicht kälter werden als die Umgebungstemperatur. Dies ist die untere Schranke bei diesem beschränkten Zerfall. Auch ein solches Verhalten kann mithilfe einer Funktion explizit dargestellt werden:

$T(t)=T_{U}+(T_{0}-T_{U})\cdot e^{-kt};~k\gt 0$

Dabei ist $T_{0}$ die Temperatur zu Beginn der Beobachtung und $T_{U}$ die Umgebungstemperatur, zum Beispiel die Raumtemperatur in dem Raum, in welchem du deinen Tee trinkst.