Logistisches Wachstum
Das Wachstum eines Bestandes ist oftmals beschränkt, zum Beispiel durch eine zur Verfügung stehende Fläche oder durch begrenzte Nahrung. Dabei kommt es zu einem charakteristischen S-förmigen Verlauf, wenn der Bestand grafisch dargestellt wird.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist logistisches Wachstum?
- Rekursive Darstellung des logistischen Wachstums
- Tabellarische Darstellung des logistischen Wachstums
- Grafische Darstellung des logistischen Wachstums
- Anwendungsbeispiel: Die Verbreitung eines Gerüchts
Was ist logistisches Wachstum?
Der Begriff logistisches Wachstum geht auf den belgischen Mathematiker Pierre-François Verhulst (1804-1849) zurück.
Er entwickelte das Modell am Beispiel des Bevölkerungswachstums. Dieses Modell veröffentlichte er 1845. Dabei ging er von einer oberen Schranke und von einer Änderungsrate vom Zeitpunkt $t$ zum Zeitpunkt $t+1$ aus. Stell dir eine Bakterienkultur in einem Glas vor: Diese wird exponentiell wachsen, aber irgendwann ist kein Platz mehr zur Ausbreitung im Glas vorhanden. Also ist das Wachstum durch eine obere Schranke beschränkt.
Die logistische Wachstumsfunktion wird allgemein mit folgender Gleichung ausgedrückt:
$ a(t)=\frac{A_{0} \cdot S}{A_{0}+(S-A_{0})\cdot e^{-Skt}} $
Dabei haben die Variablen in der Gleichung folgende Bedeutung:
- Zeit $t $
- Wachstumskonstante $k$
- die obere Schranke der Bestandsgröße $S$ (auch $G$ für Grenzbestand)
- der Anfangsbestand $A_{0} $ ( zum Zeitpunkt $t=0$)
- die Bestandsgröße $a(t) ^{=}$ (zum Zeitpunkt $t$)
Rekursive Darstellung des logistischen Wachstums
Eine Seerosenkultur verbreitet sich auf einem See. Der See hat eine Gesamtfläche von $5000~\text{m}^2$. An diesem Beispiel zum logistischen Wachstum kannst du nun die verschiedenen Darstellungsmöglichkeiten sehen.

Zu Beginn der Beobachtung bedecken die Seerosen $A(0)=3~\text{m}^2$ des Sees. Die Fläche $A(t)$ (in $\text{m}^2$), welche nach $t$ Wochen von Seerosen bedeckt wird, kann durch die folgende rekursive Darstellung des logistischen Wachstums beschrieben werden: $A(t+1)=A(t)+k\cdot A(t)\cdot (S-A(t))$
Dabei ist
- $k=0,0002$ ein Proportionalitätsfaktor und
- $S=5000~\text{m}^2$ die obere Schranke.
Tabellarische Darstellung des logistischen Wachstums
Berechne fortlaufend die bedeckte Fläche nach $t$ Wochen:
- $A(0)=3~\text{m}^2$
- $A(1)=A(0)+0,0002\cdot A(0)\cdot (5000~\text{m}^2-A(0))$
- Setze den bereits bekannten Wert $A(0)=3~\text{m}^2$ ein. So erhältst du $A(1)=3~\text{m}^2+0,0002\cdot 3~\text{m}^2\cdot (5000~\text{m}^2-3~\text{m}^2)\approx 6~\text{m}^2$
- Ab hier setzt du den gerundeten Wert in die folgenden Berechnungen ein.
- $A(2)=6~\text{m}^2+0,0002\cdot 6~\text{m}^2\cdot (5000~\text{m}^2-6~\text{m}^2)\approx 12~\text{m}^2$
- $A(3)=12~\text{m}^2+0,0002\cdot 12~\text{m}^2\cdot (5000~\text{m}^2-12~\text{m}^2)\approx24~\text{m}^2$
- $A(4)=24~\text{m}^2+0,0002\cdot 24~\text{m}^2\cdot (5000~\text{m}^2-24~\text{m}^2)\approx 48~\text{m}^2$
So kannst du fortfahren. Du kannst dann die folgende Tabelle erstellen:
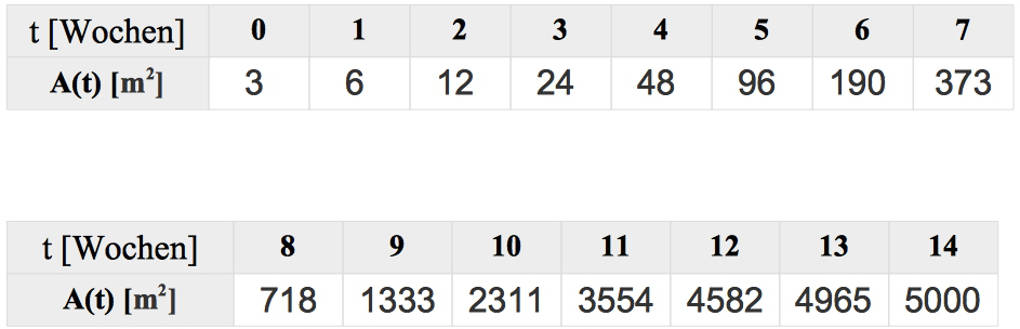
Grafische Darstellung des logistischen Wachstums
Übertrage nun diese Werte in ein Koordinatensystem.
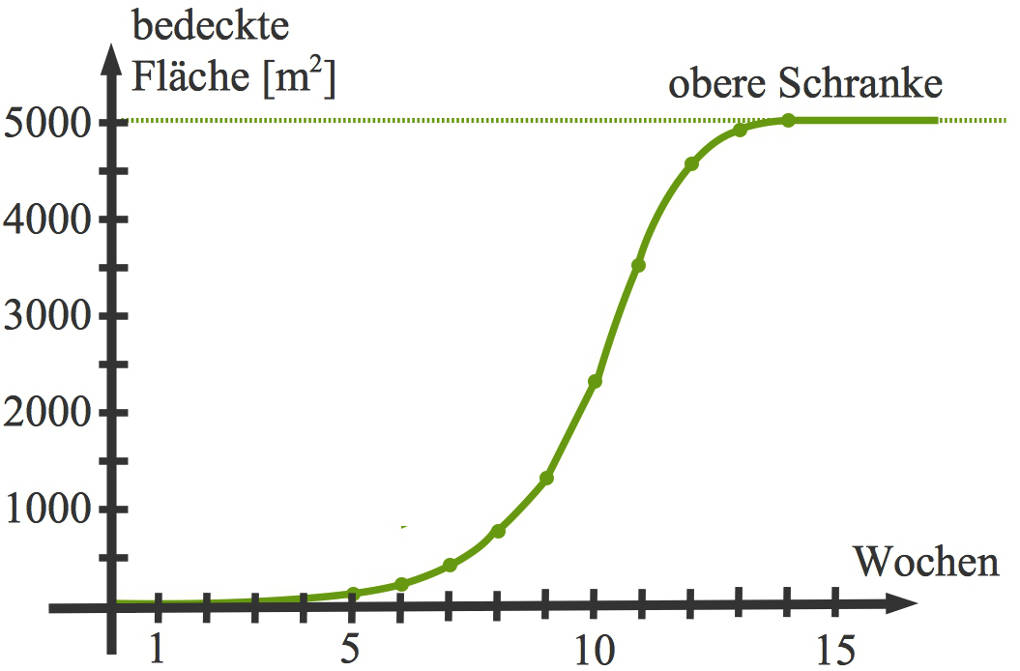
Du kannst hier den charakteristischen S-förmigen Verlauf erkennen. Nach einem anfänglichen exponentiellen Wachstum scheinen die Werte linear anzusteigen. Schließlich stagniert das Wachstum und ist nach oben begrenzt durch die obere Schranke $S=5000~\text{m}^2$.
Anwendungsbeispiel: Die Verbreitung eines Gerüchts
Auf einem Kreuzfahrtschiff befinden sich $1300$ ($S$) Menschen.
Zu Beginn der Beobachtung ($t=0$) kennen $20$ Personen ($A_{0} $) ein Gerücht. Jede dieser Personen wird dieses Gerücht am folgenden Tag einigen weiteren Personen mitteilen. So geht es weiter, bis alle Personen auf dem Schiff das Gerücht kennen.
- Am Anfang wächst die Zahl der Personen, die das Gerücht erfahren, sehr schnell an.
- Die Zahl der Personen, die das Gerücht noch nicht kennen, wird kleiner.
- Dadurch kann die Zahl der Personen, die das Gerücht erfahren, nicht dauerhaft so schnell ansteigen wie am Anfang.
- Es wird immer schwieriger, Personen zu finden, die das Gerücht noch nicht kennen.
- Die obere Schranke ist die Gesamtzahl der Personen, welche sich auf dem Kreuzfahrtschiff befinden. Diese Schranke kann mit Sicherheit nicht überschritten werden.
Du kannst diesen Zusammenhang in einem Koordinatensystem darstellen. Dabei wird auf der vertikalen Achse die Anzahl der Personen abgetragen, die das Gerücht kennen. Auf der horizontalen Achse wird die Anzahl der Tage abgetragen.
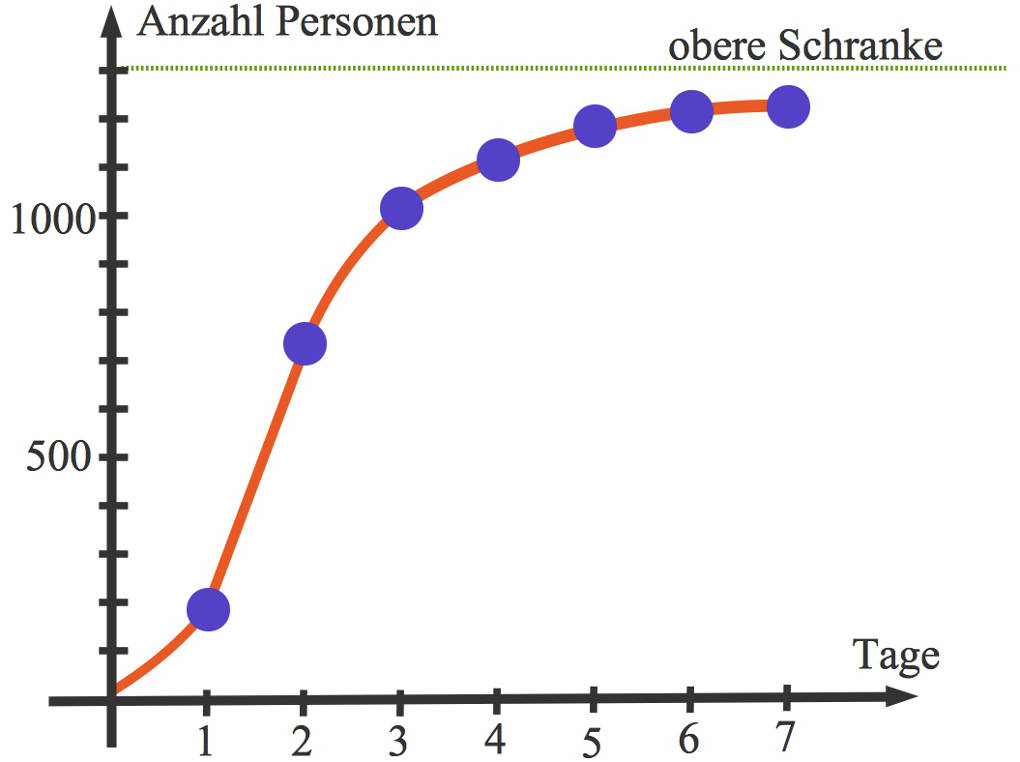
Der S-förmige Verlauf des Graphen ist charakteristisch für logistisches Wachstum.
- Zu Beginn steigt der Graph exponentiell an.
- Dann wird das Wachstum immer langsamer.
- Schließlich stagniert das Wachstum.
- Die obere Schranke wird nicht überschritten.
Alle Videos zum Thema
Videos zum Thema
Logistisches Wachstum (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Logistisches Wachstum (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter








 Logistisches Wachstum
Logistisches Wachstum
 Logistisches Wachstum – Rekursive Darstellung (1)
Logistisches Wachstum – Rekursive Darstellung (1)
 Logistisches Wachstum – Rekursive Darstellung (2)
Logistisches Wachstum – Rekursive Darstellung (2)












