Römische Zahlen und Stellenwertsysteme

Inhaltsverzeichnis zum Thema

• Die römischen Zahlen in der heutigen Alltagswelt
• Der Aufbau des römischen Zahlensystems
• Merkhilfe
• Darstellung römischer Zahlen
• Verschiedene Stellenwertsysteme im Überblick
• Das Zehnersystem
• Das Zweiersystem
• Das Fünfersystem
• Zusammenfassung

Die römischen Zahlen in der heutigen Alltagswelt

Römische Zahlen gibt es schon sehr lange. Deshalb findest du diese auch heute noch an sehr alten Gebäuden. Damit wird zum Beispiel das Baujahr angezeigt.

• An manchen Bahnhöfen gibt es noch Uhren, die die jeweiligen Stunden mit römischen Zahlen anzeigen.
• Beim Gliedern, also Ordnen, von Texten verwendet man heute auch noch häufig die römischen Zahlen. So wirst du also in den Inhaltsverzeichnissen von Büchern häufiger auf römische Zahlen treffen. Auch als Seitenzahlen der Register finden die römischen Zahlen häufiger Verwendung.
• Zudem werden sie in der Mathematik zur Einteilung von Darstellungsräumen verwendet: Die Quadranten des Koordinatensystems werden mit $I$ für den ersten, $II$ für den zweiten, $III$ für den dritten und $IV$ für den vierten Quadranten bezeichnet.

Das römische Zahlensystem geht auf Kerbschriften zurück. So wurden die Ziffern nach dem Prinzip der Fünfer- oder Zehnerbündelung angeordnet. Diese Ziffern wurden an die geschriebene Sprache angepasst. So kam es zu den folgenden Zahlzeichen:

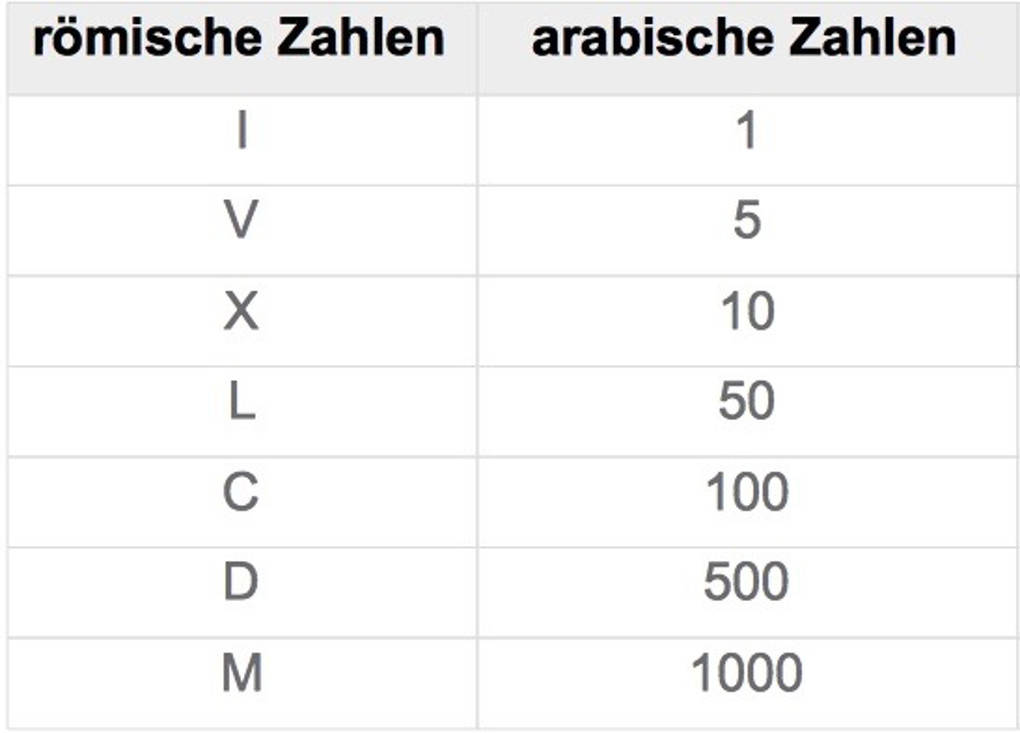
Vor etwa 500 Jahren wurden die römischen Zahlen durch die arabischen Zahlen ersetzt.

Dies sind die Zahlen, die du kennst und mit denen du rechnest. Die $500$ und auch die $1766$ sind arabische Zahlen. $MDCCLXVI$ ist eine römische Zahl.

Der Aufbau des römischen Zahlensystems

Römische Zahlen werden aus den oben angegebenen Zahlzeichen zusammengesetzt. Dabei ergibt sich der jeweilige Zahlwert durch Addition (oder Subtraktion) der einzelnen Werte der Ziffern von links nach rechts. Die römische Zahlschrift ist somit eine additive Zahlschrift. Deshalb gibt es bei den römischen Zahlen auch keine $\mathbf{0}$.

Die römischen Zahlen werden nach bestimmten Regeln zusammengesetzt:

• Die Dreizeichenregel: Jedes Zeichen wird maximal dreimal hintereinandergeschrieben.
• Die Additionsregel: Steht ein kleineres Zahlzeichen hinter einem größeren, so wird der entsprechende Wert addiert: $XI$ steht für $10+1=11$.
• Die Subtraktionsregel: Steht ein kleineres Zahlzeichen vor einem größeren, so wird der entsprechende Wert subtrahiert: $IX$ steht für $10-1=9$.

Im Gegensatz zu dem arabischen Zahlensystem ist das römische Zahlensystem kein Stellenwertsystem. Das bedeutet, dass das Symbol $V$ immer für die Zahl $5$ steht. Beim arabischen Zahlensystem ist die Bedeutung der $5$ abhängig von der Stelle, an welcher diese sich befindet. So steht die $5$ in $525$ einmal für die Hunderter und einmal für die Einer.

Merkhilfe

Die folgende Abbildung stellt die römischen Zahlen in aufsteigender Reihenfolge in einem Merksatz zusammen. Es werden die Zahlen $I=1$ bis $M=1000$ dargestellt.

Darstellung römischer Zahlen

Um römische Zahlen in arabische Ziffern umzurechnen, musst du die Bedeutung der römischen Zahlsymbole kennen. Versuche es einmal anhand dieser Beispiele selbst nachzurechnen:

• $I$ steht für $1$
• $II$ steht für $1+1=2$
• $III$ steht für $1+1+1=3$
• Statt $IIII$ schreibt man $IV$ für $5-1=4$
• $XVII$ steht für $10+5+1+1=17$
• $LXIX$ steht für $50+10+10-1=69$
• $CC$ steht für $100+100=200$
• $MDCCLXVI$ steht für $1000+500+100+100+50+10+5+1=1766$
• $MMXVI$ steht für $1000+1000+10+5+1=2016$
• $CMXCIX$ steht für $1000-100+100-10+10-1=999$

Willst du umgekehrt eine arabische Zahl als römische Zahl schreiben, dann gehst du wie folgt vor:

Am Beispiel $1965$

• Für die $1000$ verwendest du das Symbol $M$.
• Denke an die Dreizeichenregel. $900$ wird nicht als $DCCCC$ geschrieben, sondern als $CM$ für $1000-100=900$.
• Die $60$ ergibt sich durch Addition $50+10$ und somit als römische Zahl $LX$.
• Die $5$ am Ende entspricht dem Symbol $V$.

Damit kannst du $1965$ als römische Zahl wie folgt schreiben $MCMLXV$.

Probier doch mal, dein Geburtsjahr als römische Zahl zu schreiben.

Verschiedene Stellenwertsysteme im Überblick

Du lernst in der Schule Zahlen kennen. Dabei beginnst du mit Zahlen bis $10$, dann kommen größere Zahlen hinzu, bis $100$ oder sogar bis zu $1.000.000$ (einer Million). All diese Zahlen haben gemeinsam, dass ihre Stellen jeweils Zehnerpotenzen sind. Das bedeutet, dass die Stellen jeweils Potenzen mit der Basis $10$ sind, also zum Beispiel $ 10^{2} = 100 $ .

Die Basis kann aber auch jede andere Zahl sein, zum Beispiel die $2$ oder die $5$. Du kannst dir auch gerne ein weiteres Stellenwertsystem mit deiner Lieblingszahl als Basis einfallen lassen.

Das Zehnersystem

Du kannst an deinen Fingern immer bis $10$ abzählen. Deshalb lernst du die Zahlen, so wie sie üblicherweise auch aufgeschrieben werden, im Zehnersystem kennen. Dieses System wird auch als Dezimalsystem bezeichnet. Diese Bezeichnung kommt von dem lateinischen Wort „decem“ für „zehn“.

Für Zahlen im Zehnersystem werden die Ziffern von $0$ bis $9$ verwendet. Die jeweiligen Stellen im Zehnersystem sind Zehnerpotenzen:

$\begin{array}{cccc} 10^0&=&1&~&10^3&=&1000&~\\ 10^1&=&10&~&10^4&=&10000&~\\ 10^2&=&100 &~&10^5&=&100000&~ \end{array}$

Schau dir ein Beispiel an:

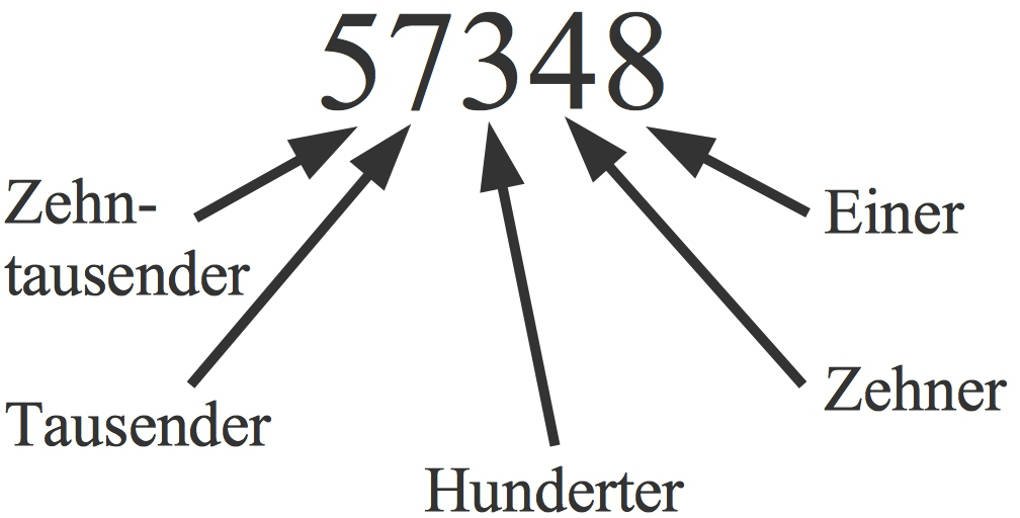
Diese Zahl kannst du auch so schreiben:

$57348=5\cdot 10^{4}+7\cdot 10^{3}+3\cdot 10^{2}+4\cdot 10^{1}+8\cdot 10^{0}$.

Das Zweiersystem

Im Zweiersystem werden nur die Ziffern $0$ und $1$ verwendet. Computer rechnen auf diese Weise. Dabei bedeutet die $0$ einfach “Strom aus” und die $1$ “Strom an”. Das Zweiersystem wird auch als Binärsystem oder Dualsystem bezeichnet.

Dieses System ist sehr alt, es lässt sich zurückverfolgen bis ins 3. Jahrhundert v.Chr. Gottfried Wilhelm Leibniz, ein deutscher Mathematiker, beschrieb das System am Anfang des 18. Jahrhunderts ausführlich.

Die Stellen in diesem System sind Zweierpotenzen:

$\begin{array}{cccc} 2^0&=&1&~&2^3&=&8&~\\ 2^1&=&2&~&2^4&=&16&~\\ 2^2&=&4 &~&2^5&=&32&~ \end{array}$

Genauso wie im Dezimalsystem, kannst du jede Zahl als Summe von Produkten schreiben. Allerdings wird hier jeweils eine Zweierpotenz entweder mit $0$ oder mit $1$ multipliziert.

Sieh dir als Beispiel die Umrechnung der Zahl $55$ an:

• Schreibe zunächst $55$ als Summe von Zweierpotenzen: $55=32+16+4+2+1$.
• Schreibe jeden Summand als Produkt: $55=1\cdot 2^{5}+1\cdot 2^{4}+1\cdot 2^{2}+1\cdot 2^{1}+1\cdot 2^{0}$.
• Du siehst, die Potenz $2^{3}$ fehlt. Hier schreibst du $0\cdot 2^{3}$.
• Gesamt erhältst du dann: $55=1\cdot 2^{5}+1\cdot 2^{4}+0\cdot 2^{3}+1\cdot 2^{2}+1\cdot 2^{1}+1\cdot 2^{0}$.
• Wie beim Dezimalsystem, lässt du nun die Potenzen weg. Dies führt zu der Zahl $110111$, welche im Binärsystem für die Zahl $55$ des Dezimalsystems steht.

Das Fünfersystem

Ebenso wie die beiden nun bereits bekannten Stellenwertsysteme ist das Fünfersystem aufgebaut:

Die Stellen sind Fünferpotenzen:

$\begin{array}{cccc} 5^0&=&1&~&5^3&=&125&~\\ 5^1&=&5&~&5^4&=&625&~\\ 5^2&=&25 &~&5^5&=&3125&~ \end{array}$

Die verwendeten Ziffern sind die Ziffern von $0$ bis $4$.

Wir schreiben nun die $55$ im Fünfersystem:

• $55=2\cdot 25+5$
• $55=2\cdot 5^{2}+1\cdot 5^{1}+0\cdot 5^{0}$
• Damit ist die Darstellung von $55$ im Fünfersystem vollständig: $210$.

Zusammenfassung

Um zu wissen, welche Zahl du gerade vor dir hast, solltest du also wissen, in welchem Zahlensystem die Zahl geschrieben ist:

• Die Zahl $55$ im Dezimalsystem ist
• die Zahl $110111$ im Binärsystem und
• $210$ im Fünfersystem.

Wenn du am $25.10.2002$ geboren bist, dann ist

• der Tag im Binärsystem $11001$,
• der Monat im Fünfersystem $20$ und
• das Jahr lassen wir mal lieber im Dezimalsystem.

Du bist also am $11001.20.2002$ geboren. Aber das ist ja eigentlich Unsinn und das versteht auch keiner, da drei verschiedene Stellenwertsysteme verwendet werden.