Satz von der totalen Wahrscheinlichkeit
In der Stochastik geht es oftmals auch darum, ob Ereignisse einander bedingen. Um dies zu prüfen, berechnest du unter anderem die totale Wahrscheinlichkeit für das Eintreten eines Ereignisses.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Satz von der totalen Wahrscheinlichkeit von zwei Ereignissen
- Herleitung des Satzes von der totalen Wahrscheinlichkeit
- Ausblick: Satz von der totalen Wahrscheinlichkeit für mehrere Ereignisse
Satz von der totalen Wahrscheinlichkeit von zwei Ereignissen
Gegeben ist ein zweistufiges Zufallsexperiment mit den beiden Ereignissen $A$ und $B$. Weiterhin sind die Wahrscheinlichkeiten $P(A)$ und $P(\overline{A})$ (Gegenwahrscheinlichkeit bekannt. Das Eintreten des Ereignisses $B$ hängt vom Eintreten des Ereignisses $A$ ab. Bei einer solchen Abhängigkeit spricht man von einer bedingten Wahrscheinlichkeit**. Die Wahrscheinlichkeit, dass Ereignis $B$ eintritt unter der Voraussetzung, dass Ereignis $A$ bereits eingetreten ist, bezeichnet man wie folgt:
$P(B|A)$
Um das Zufallsexperiment zu veranschaulichen, kannst du dir ein solches Baumdiagramm erstellen:
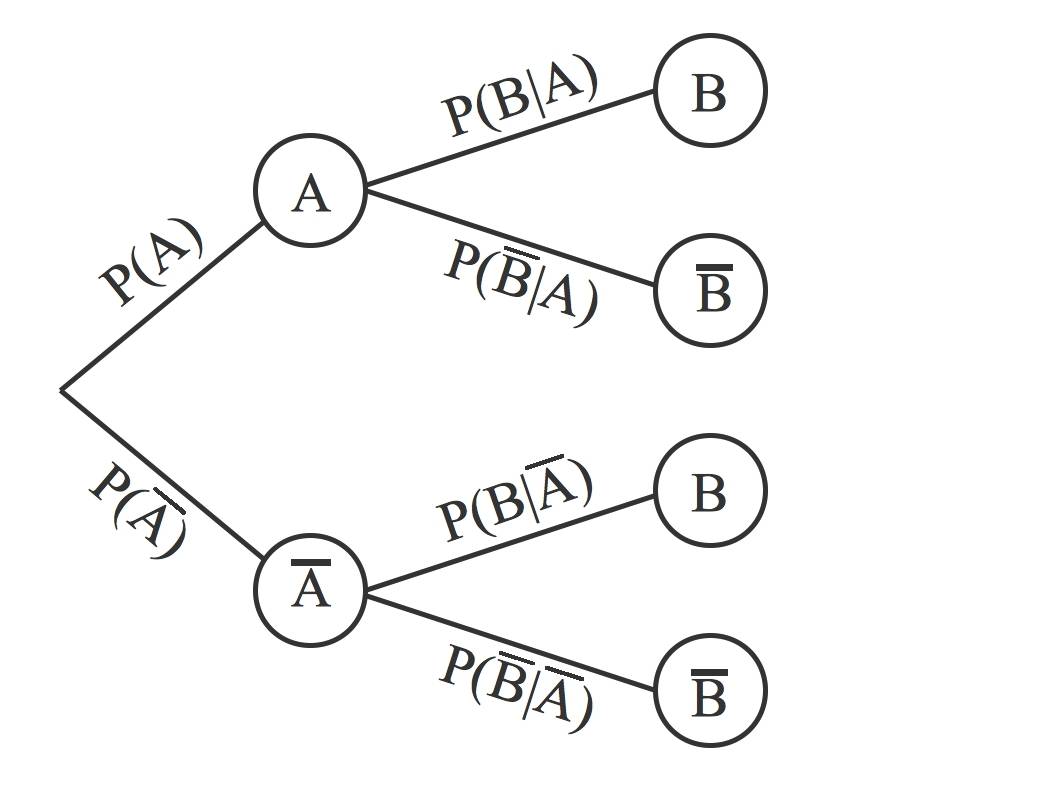
Der Satz von der totalen Wahrscheinlichkeit gibt dir die Antwort auf die Frage, wie groß die Wahrscheinlichkeit für das Eintreten des Ereignisses $B$ insgesamt ist.
Bedingte Wahrscheinlichkeiten
Vieles, was du tust, hängt von deiner Vorbereitung ab. Hast du viel für eine Mathematik-Arbeit gelernt, erhöht sich die Chance, dass du eine gute Note erreichst. Solche Abhängigkeiten gibt es auch in der Stochastik. Dies führt uns zu dem Begriff der bedingten Wahrscheinlichkeit.
Mache dir dies einmal an einem Beispiel klar:
Mit $60\%$-iger Wahrscheinlichkeit soll es am Sonntag wärmer als $25°C$ werden. Der Besitzer der Eisdiele „Eisdealer“ weiß, dass mit $80\%$-iger Wahrscheinlichkeit mehr als $100$ Gäste kommen, wenn es wärmer als $25°$ ist. Andernfalls kommen mit $35\%$-iger Wahrscheinlichkeit mehr als $100$ Gäste. Du siehst, die Wahrscheinlichkeit dafür, dass mehr als $100$ Gäste kommen, hängt von den Temperaturen ab.
Du betrachtest nun die folgenden Ereignisse:
- $A$: Es ist wärmer als $25°$.
- $B$: Es kommen mehr als $100$ Gäste.
Dann kannst du die folgenden Wahrscheinlichkeiten aus den obigen Informationen ablesen:
- $P(A)=0,6$ und $P(\overline{A})=0,4$
- $P(B|A)=0,8$ sowie $P(B|\overline{A})=0,35$
Diesen Zusammenhang kannst du dir auch anhand von Flächen klarmachen:
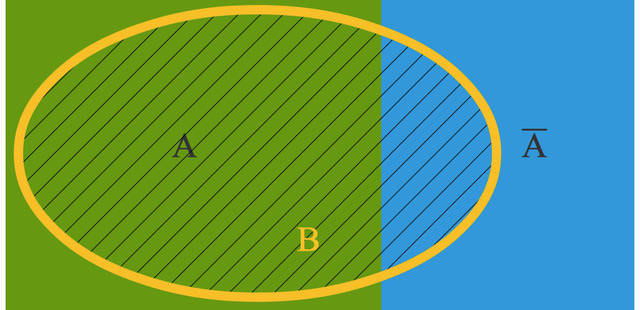
- Das gesamte Rechteck steht für die Grundmenge $\Omega$ mit $P(\Omega)=1$.
- Die Anteil der grünen Fläche an der Grundmenge steht für $P(A)$ und der der blauen für $P(\overline{A})$.
- Da $A\cap \overline{A}=\emptyset$ und $A\cup \overline{A}=\Omega$ ist, gilt $P(A)+P(\overline{A})=1$. Wenn zwei Mengen, hier $A$ und $\overline{A}$, keine gemeinsamen Elemente haben, werden sie als disjunkt bezeichnet.
- Der Flächenanteil der schraffierten Ellipse an der grünen Fläche entspricht $P(B|A)$ und der an der blauen Fläche $P(B|\overline{A})$.
- Der Flächenanteil der Ellipse an der Grundmenge entspricht der Wahrscheinlichkeit für das Eintreten des Ereignisses $B$ insgesamt. Dies ist die totale Wahrscheinlichkeit.
Herleitung des Satzes von der totalen Wahrscheinlichkeit
Wie kann nun die totale Wahrscheinlichkeit eines Ereignisses verwendet werden? Dies kannst du dir anhand eines Baumdiagramms und anhand der Darstellung der Flächen klarmachen. Hier siehst du die Herleitung mithilfe eines Baumdiagramms sowie der 1. Pfadregel (auch: Produktregel) sowie der 2. Pfadregel (auch: Summenregel).
Betrachte hierfür noch einmal das obige Baumdiagramm:

Du kannst anhand dieses Baumdiagramms erkennen, dass du über zwei Pfade zu dem Ereignis $B$ gelangst: Entweder über $A$ oder über $\overline{A}$.
Mithilfe der ersten Pfadregel kannst du nun die Wahrscheinlichkeiten berechnen, indem du diese entlang des Pfades multiplizierst:
- $P(A\cap B)=P(A)\cdot P(B|A)$
- $P(\overline{A}\cap B)=P(\overline{A})\cdot P(B|\overline{A})$
Dies wird auch als Multiplikationssatz bezeichnet.
Nun kannst du die so erhaltenen Wahrscheinlichkeiten addieren. Dies ist die zweite Pfadregel. So erhältst du
$P(B)=P(A)\cdot P(B|A)+P(\overline{A})\cdot P(B|\overline{A})$.
Dies ist der Satz von der totalen Wahrscheinlichkeit.
Satz von der totalen Wahrscheinlichkeit – Anwendung
Kommen wir wieder zu dem Beispiel der Eisdiele zurück. Du möchtest unabhängig vom Wetter berechnen, wie groß die Wahrscheinlichkeit ist, dass am kommenden Sonntag mehr als $100$ Gäste kommen. Du möchtest also die totale Wahrscheinlichkeit für das Ereignis $B$ berechnen. Wende hierfür den Satz von der totalen Wahrscheinlichkeit an:
$P(B)=0,6\cdot 0,8+0,4\cdot 0,35=0,62$
Das heißt, dass am kommenden Sonntag mit einer Wahrscheinlichkeit von $62\%$ mehr als $100$ Gäste in den „Eisdealer“ kommen.
Der Satz von Bayes
Du könntest dich nun auch fragen, wie groß die Wahrscheinlichkeit ist, dass es wärmer als $25°$ Grad ist, wenn du weißt, dass mehr als $100$ Gäste im „Eisdealer“ zu Besuch sind. Gesucht ist dieses Mal die bedingte Wahrscheinlichkeit $P(A|B)$. Beachte die unterschiedliche Reihenfolge der Ereignisse. Diese Wahrscheinlichkeit berechnest du mit dem Satz von Bayes:
$P(A|B)=\frac{P(A)\cdot P(B|A)}{P(A)\cdot P(B|A)+P(\overline{A})\cdot P(B|\overline{A})}$
Setze nun die bekannten Wahrscheinlichkeiten ein. So kommst du zu
$P(A|B)=\frac{0,6\cdot 0,8}{0,6\cdot 0,8+0,4\cdot 0,35}=\frac{0,48}{0,62}\approx 0,7742$.
Wenn also mehr als $100$ Gäste im „Eisdealer“ zu Besuch sind, ist die Wahrscheinlichkeit dafür, dass es wärmer als $25°$ ist, ungefähr $77\%$.
Ausblick: Satz von der totalen Wahrscheinlichkeit für mehrere Ereignisse
Die Idee der totalen Wahrscheinlichkeit lässt sich auf mehr als zwei Ereignisse übertragen. In der allgemeinen Form lautet die Gleichung:
$P(B)=\sum\limits_{i=1}^n P(A_{i})\cdot P(B|A_{i})$
Dabei müssen die Ereignisse $A_{i}$ paarweise disjunkt sein. Das heißt, dass die Schnittmenge aus zwei Ereignissen $A_i$ und $A_j$ für alle $i\neq j$ leer ist.
Im Folgenden siehst du eine Veranschaulichung für den Fall $n=5$. Das bedeutet, dass es $5$ solcher $A_i$ gibt. Diese nennen wir $A_1, A_2, A_3, A_4$ und $A_5$. Um dir einen besseren Überblick zu geben, siehst du dazu eine grafische Darstellung. Beachte, dass diese $A_i$ disjunkt sind, da die Flächen sich nicht gegenseitig überdecken:

Der jeweilige Anteil der Fläche der Ellipse, für das Ereignis $B$, an den Flächen der einzelnen Rechtecke steht für die entsprechenden bedingten Wahrscheinlichkeiten $P(B|A_{i})$, $1\le i\le 5$.
Dann gilt nach dem Satz von der totalen Wahrscheinlichkeit:
$P(B)=\sum\limits_{i=1}^5 P(A_{i})\cdot P(B|A_{i})$
Alle Videos zum Thema
Videos zum Thema
Satz von der totalen Wahrscheinlichkeit (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Satz von der totalen Wahrscheinlichkeit (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter




 Satz von der totalen Wahrscheinlichkeit – Einführung
Satz von der totalen Wahrscheinlichkeit – Einführung












