Zufallsexperimente
Das Ergebnis eines Zufallsexperimentes ist nicht vorhersehbar und viele solcher Experimente sind im Alltag zu beobachten.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist ein Zufallsversuch?
Eine Entscheidung ohne Wissen ist eine zufällige Entscheidung.
Als Zufallsversuch beziehungsweise Zufallsexperiment bezeichnen wir einen Vorgang mit einer zufälligen Entscheidung.
Das, was dabei herauskommt, ist ein Ergebnis. Dieses können wir als möglichen Endzustand eines Zufallsversuchs betrachten. Die Ergebnismenge ist die Menge aller Ergebnisse eines Zufallsversuchs.
Definition:
Ein Vorgang ist ein Zufallsversuch, wenn
- mindestens zwei Ergebnisse möglich sind,
- er beliebig oft wiederholt werden kann und
- die Ergebnisse nicht vorhersehbar sind.
Es gibt Zufallsversuche, die nur einmal durchgeführt werden und solche, die wiederholt werden.
Wir sprechen dann von einstufigen und mehrstufigen Zufallsexperimenten.
Eine Münze wird einmal geworfen. Die möglichen Ergebnisse sind Kopf oder Zahl.

Aus einer Urne wird mehrmals hintereinander eine Kugel gezogen. Welche Farbe als nächstes kommt, ist absolut zufällig.
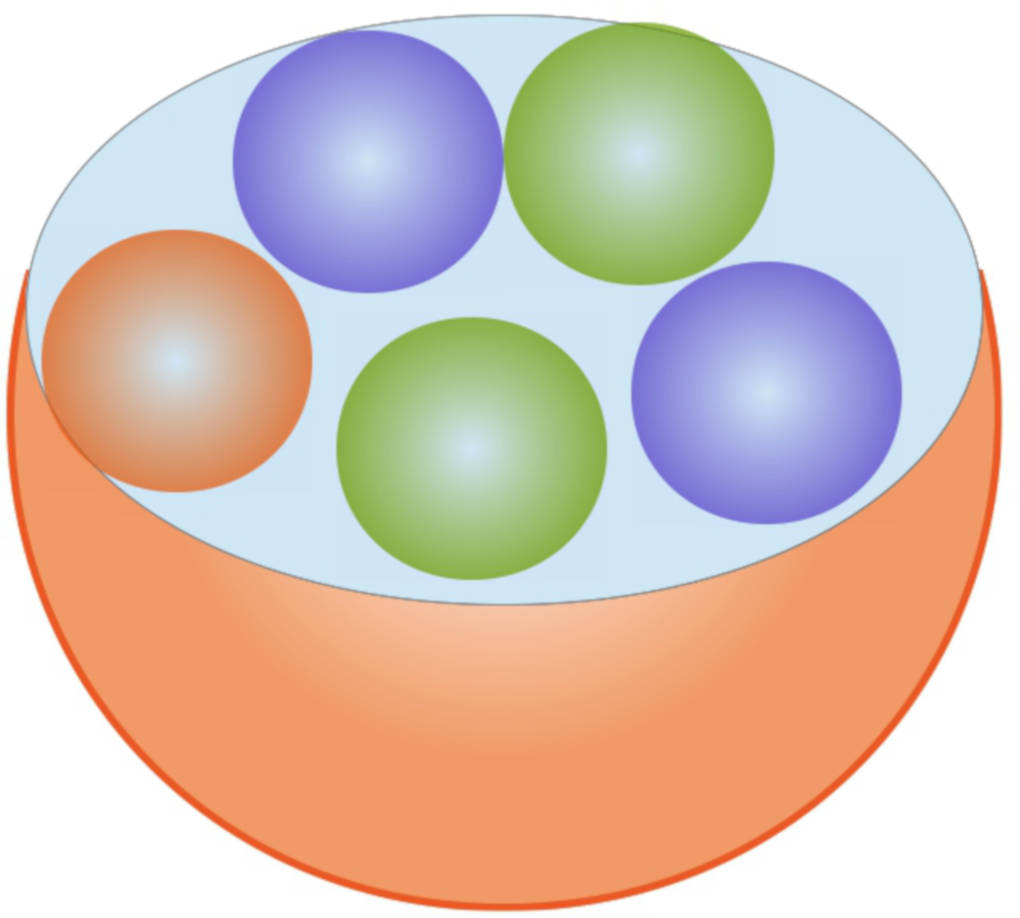
Beispiele für Zufallsexperimente
Mit Zufallsexperimenten verbindet man in erster Linie Glücksspiele. Die Ergebnisse kommen durch zufällige Entscheidungen zustande und sind daher nicht vorhersehbar.
Dies trifft sowohl auf den Münzwurf als auch auf das Urnenexperiment zu, da man nicht weiß, wie man werfen beziehungsweise ziehen muss, um das gewünschte Ergebnis zu erhalten.
Im Folgenden sind weitere Beispiele für Glücksspiele aufgeführt:
Würfeln:
Jede der sechs Augenzahlen aus der Ergebnismenge kann gewürfelt werden. Welche diese ist, hängt vom Zufall ab.

Karten ziehen:
Wenn aus drei Karten zufällig eine gezogen wird, ist nicht vorhersehbar, welche diese sein wird.

Roulette:
Bei diesem bekannten Glücksspiel wird eine Kugel geworfen, die sich solange dreht, bis sie auf einem der Felder mit den Zahlen von $1$ bis $36$ oder $0$ oder $00$ landet. Auch hier ist das Ergebnis nicht vorhersagbar.

Lotto:
Das Ziehen der Lottozahlen hängt davon ab, welche sechs der $49$ Kugeln zufällig von der Maschine gezogen werden. Das Prinzip entspricht dem der Urne.
Ziehen von Losen:
Da vor dem Ziehen nicht ersichtlich ist, welche Lose Gewinne und welche Nieten darstellen, handelt es sich auch hier um einen Zufallsversuch.
Aber auch in anderen Bereichen spielen Zufallsversuche eine wichtige Rolle: In Meinungsumfragen werden zufällig Leute ausgewählt, die zufällige Antworten geben. Bei der Vererbung kommt eine zufällige Kombination von Genen zustande, die man nicht beeinflussen kann.
Es gibt auch Zufallsversuche, die nicht ganz eindeutig erscheinen:
Spielautomaten:
Ist es wirklich zufällig, welche Zahlen oder Symbole als Ergebnis erscheinen? Welcher Mechanismus steckt dahinter?

Sportwettkämpfe:
Wenn alle Sportler bezogen auf ihre Vorleistung gleich gut sind, wovon hängt der Sieg dann ab? Von der Tagesform oder Zufällen im Verlauf des Wettbewerbs?

Alle Videos zum Thema
Videos zum Thema
Zufallsexperimente (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Zufallsexperimente (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter




 Zufallszahlen
Zufallszahlen









