Brüche kürzen und erweitern

Inhaltsverzeichnis zum Thema

• Was ist ein Bruch?
• Brüche erweitern
• Beispiele
• Brüche kürzen
• Beispiele

Was ist ein Bruch?

Was Brüche sind, kannst du dir gut an einem Beispiel klarmachen.

Lisa hat Geburtstag und bekommt ihren heißgeliebten Erdbeerkuchen.

Der Vater teilt den Kuchen in $12$ gleich große Stücke auf. Lisa geht mit ihren vier Freundinnen auf ihr Zimmer und jedes Mädchen nimmt genau ein Stück Kuchen, also ein Teil des Ganzen mit. Insgesamt nehmen die fünf Freundinnen also $5$ von $12$ Stücken Kuchen oder auch fünf Zwölftel des Kuchens mit. Dies kann man so schreiben.

Oben steht eine Zahl und unten ebenfalls. Dazwischen befindet sich ein Strich.

• Der Strich ist der Bruchstrich. Er zeigt an, dass geteilt wird, genau wie das Geteiltzeichen oder Divisionszeichen.
• Die Zahl unter dem Bruchstrich ist der Nenner. Sie benennt den Bruch, hier zum Beispiel „Zwölftel“. Der Nenner gibt also an, in wie viele Teile ein Ganzes geteilt wurde.
• Die Zahl über dem Bruchstrich ist der Zähler. Sie gibt an, wie viele der Teile ausgewählt wurden, also wie viele Stücke Kuchen die Freundinnen mit auf das Zimmer nehmen.

Du kannst einen solchen Bruch auch als Bruchstreifen darstellen.

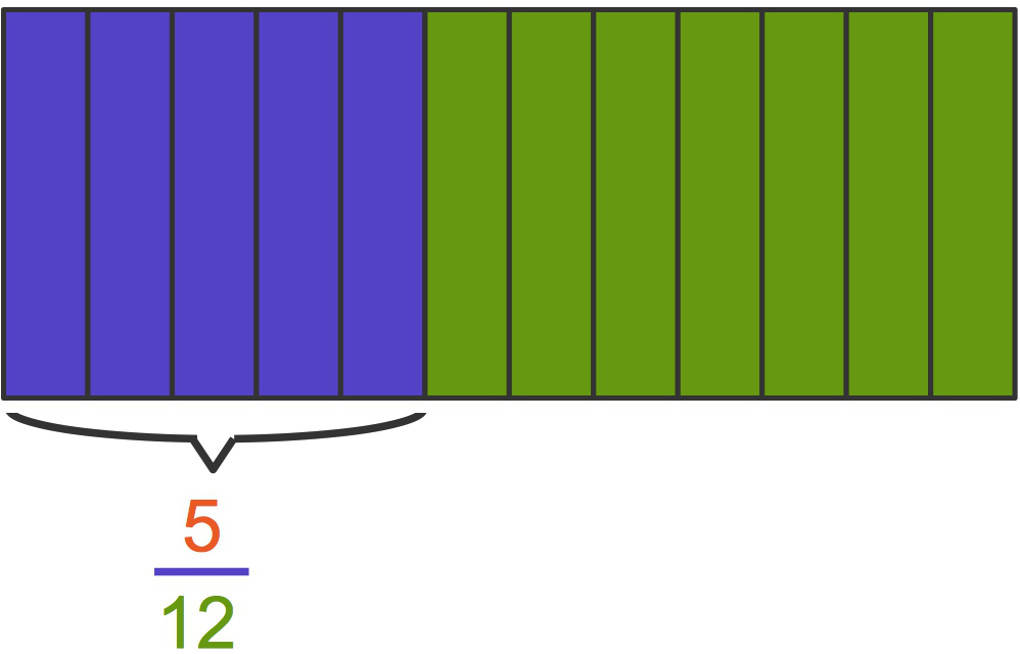
Das gesamte große Rechteck ist ein Ganzes. Jedes der kleinen Rechtecke ist ein Zwölftel. Blau markiert sind fünf dieser Zwölftel.

Der Nenner eines Bruches ist sozusagen die Maßeinheit bei Brüchen.

Oft ist es wichtig, Brüche mit der gleichen Maßeinheit zu haben, also Brüche mit einem gemeinsamen Nenner. Haben Brüche denselben Nenner, so bezeichnet man sie als gleichnamig. Gleichnamige Brüche sind zum Beispiel in diesen Fällen wichtig:

• Wenn du einen Größenvergleich bei Brüchen durchführen willst.
• Wenn du Brüche addieren oder Brüche subtrahieren möchtest.

Wenn Brüche nicht gleichnamig sind, also keinen gemeinsamen Nenner haben, kannst du sie trotzdem vergleichen, addieren oder subtrahieren. Hierfür musst du die Brüche auf einen gemeinsamen Nenner bringen.

Dafür wiederum musst du Brüche erweitern oder kürzen.

Brüche erweitern

Brüche erweitern kannst du, indem du sowohl den Zähler als auch den Nenner mit derselben Zahl multiplizierst. Der Wert des Bruches bleibt dabei erhalten, weil du das Ganze in mehr Teile teilst (zum Beispiel dreimal so viele Teile), dafür aber auch mehr Teile auswählst (auch dreimal so viele).

Hier siehst du ein Beispiel:

$\frac5{12}=\frac{5\cdot 3}{12\cdot 3}=\frac{15}{36}$

Auch dies kannst du dir an einem Bruchstreifen klarmachen:

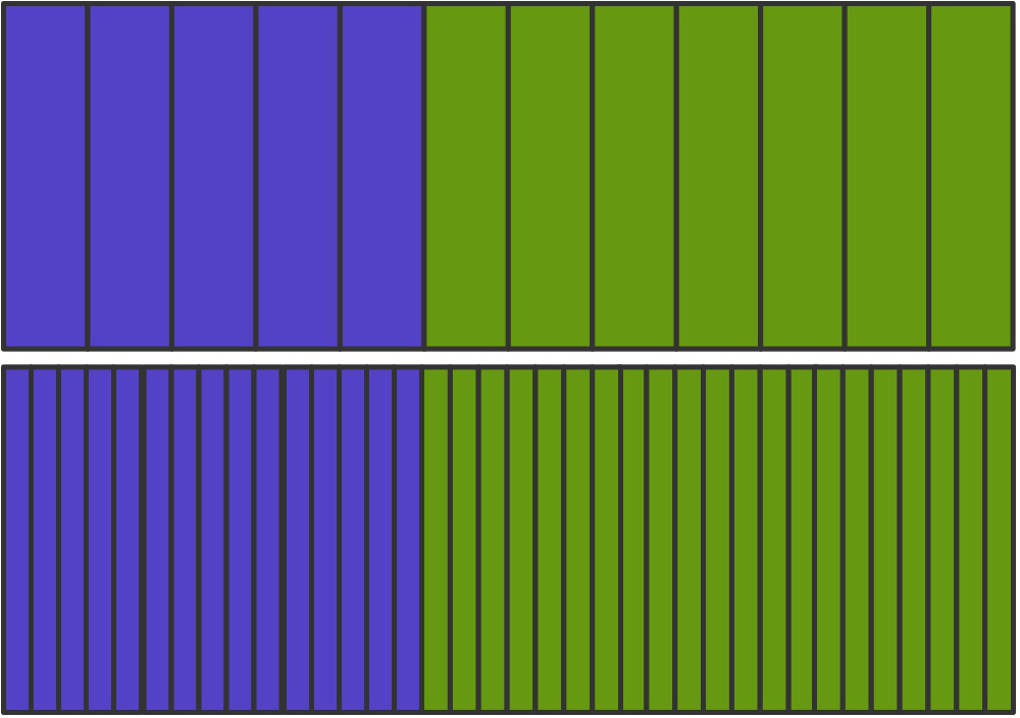
Du siehst: Der blau markierte Anteil besteht aus $15$ Rechtecken. Jedes dieser Rechtecke ist ein $36$-tel des gesamten Rechtecks.

Beispiele

$\frac23=\frac{2\cdot 6}{3\cdot 6}=\frac{12}{18}$

$\frac15=\frac{1\cdot 5}{5\cdot 5}=\frac{5}{25}$

$\frac57=\frac{5\cdot 3}{7\cdot 3}=\frac{15}{21}$

Brüche kürzen

Indem du sowohl den Zähler als auch denn Nenner durch denselben Faktor dividierst (teilst), kannst du Brüche kürzen. Auch hier bleibt der Wert des Bruches erhalten, wichtig ist aber, dass du eine Zahl wählst, die von Nenner und Zähler ein Faktor ist. Schau dir das Beispiel an:

$\frac{3}{12}=\frac{3:3}{12:3}=\frac1{4}$

Auch dies kannst du dir anschaulich an einem Kuchen klarmachen.

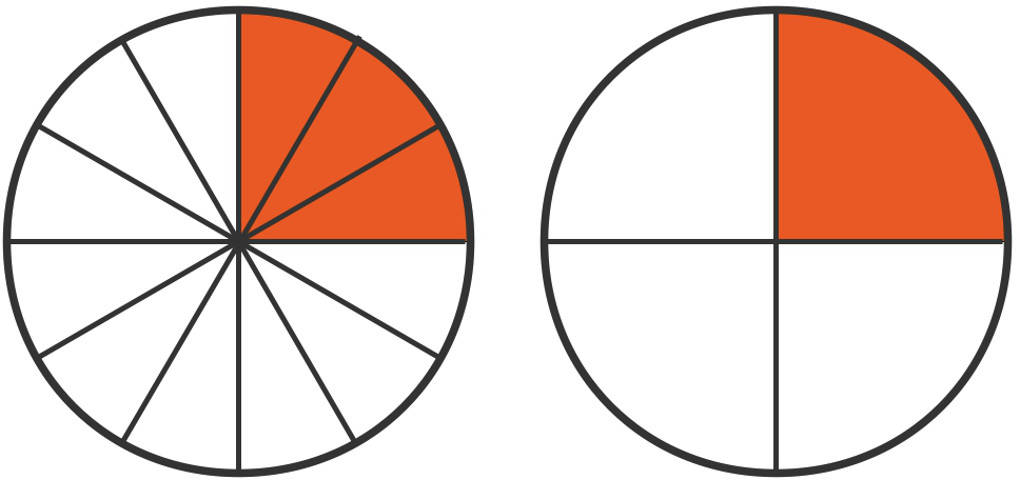
Links siehst du drei Zwölftel des ganzen Kreises (Kuchens) und rechts ein Viertel. Du erkennst, dass die beiden rot markierten Stücke gleich groß sind.

Beispiele

Als Beispiele kannst du hier jeweils die Umkehrung der obigen Beispiele zum Erweitern anschauen.

$\frac{12}{18}=\frac{12:2}{18:2}=\frac69=\frac{6:3}{9:3}=\frac23$

Du siehst, du kannst auch mehrmals kürzen. Dies tust du so lange, bis Zähler und Nenner keine gemeinsamen Faktoren mehr haben. Das bedeutet, du kürzt einen Bruch immer so weit als möglich.

$\frac{5}{25}=\frac{5:5}{25:5}=\frac15$

$\frac{15}{21}=\frac{15:3}{21:3}=\frac57$