Arbeiten mit dem Geodreieck: Geraden, Strecken und Winkel
Wo bin ich? Wo bist du?
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Wo bist du?
- Eine Position genau beschreiben
- Wege und Richtungen
- Parallele Linien
- Senkrechte Linien
- Arbeit mit dem Geodreieck
Wo bist du?
Paul geht mit seiner Familie spazieren. Sein Vater geht über eine Brücke. Paul bleibt mit seiner Schwester Meike am Fluss und wirft Steinchen hinein.

Paul und seine Schwester sind unten und ihr Vater oben.
Nun kommt ihr Vater zu den beiden an den Fluss und stellt sich zwischen sie. Er steht nun in der Mitte von Paul und seiner Schwester. Paul und seine Schwester stehen links und rechts von ihrem Vater.
Meike möchte mit ihrer neuen Kamera ein Foto von ihrem Bruder und ihren Eltern machen.

- Auf diesem Foto steht Paul vor seinen Eltern. Seine Eltern stehen also hinter ihm.
- Von dir aus gesehen steht Pauls Vater rechts von der Mutter. Somit steht Pauls Mutter links von seinem Vater.
Wie kannst du eigentlich links und rechts unterscheiden? Du hast sicher eine Hand, mit der du besser schreiben kannst als mit der anderen. Es gibt Linkshänder, die schreiben mit links, und es gibt Rechtshänder, die schreiben mit rechts. Du kannst dich also immer daran orientieren, mit welcher Hand du schreibst. Dafür musst du dir nur merken, ob du Rechts- oder Linkshänder bist.
Hier im Bild siehst du eine Hand, die schreibt. Dies ist eine rechte Hand.
Eine Position genau beschreiben
Wenn du möglichst genau beschreiben willst, wo sich ein Gegenstand (oder eine Person) gerade befindet, dann beantwortest du immer drei Fragen:
- Befindet sich der Gegenstand vor oder hinter mir?
- Befindet sich der Gegenstand rechts oder links von mir?
- Befindet sich der Gegenstand über oder unter mir?
Die letzte Frage könnte dir zum Beispiel jemand stellen, wenn du dich in einem mehrstöckigen Haus befindest.
Auf jede Frage hast du drei Antwortmöglichkeiten. Auf die dritte Frage kannst du zum Beispiel Folgendes antworten:
- „Der Gegenstand ist über mir.“
- „Der Gegenstand ist unter mir.“
- „Der Gegenstand ist auf der gleichen Höhe wie ich.“
Es kann schließlich auch sein, dass sich ein Gegenstand im gleichen Stockwerk wie du befindet. Dann ist er aber weder über noch unter dir, sondern in der Mitte, also auf gleicher Höhe wie du.
Du kannst die Position eines Gegenstandes auch durch die eines zweiten Gegenstandes ausdrücken. Man sagt dann, dass sich die beiden Gegenstände in bestimmten Positionen relativ zueinander befinden. Dann lauten die drei Fragen:
- Ist der erste Gegenstand vor oder hinter dem zweiten Gegenstand?
- Ist der erste Gegenstand rechts oder links vom zweiten Gegenstand?
- Ist der erste Gegenstand über oder unter dem zweiten Gegenstand?
Und wenn du sogar mehr als zwei Gegenstände (oder wie hier, Personen) hast, dann kannst du gewisse Erklärungen noch ein wenig abkürzen. Anstatt zum Beispiel „Pauls Vater steht links von Paul und rechts von Meike“ zu sagen, geht auch „Pauls Vater steht zwischen Paul und Meike.“
Wege und Richtungen
Meike und Paul gehen von der Brücke aus weiter spazieren. Sie laufen ein kurzes Stück geradeaus. Nach einer Weile kommen sie an einen Weg, der ihren kreuzt. Sie können nun nach links oder nach rechts gehen. Paul entscheidet sich, nach links zu gehen. Meike und die Eltern der beiden folgen Paul. Alle sind gespannt, wo sie wohl hinkommen.
Sie kommen zu einem Hochsitz. Den benutzen Förster, um die Tiere im Wald zu beobachten. Meike ist ganz neugierig. Sie möchte auf den Hochsitz hinaufklettern. Ihr Vater geht mit ihr mit. Nun sind Meike und ihr Vater oben und Paul mit seiner Mutter unten. Nach einer Weile kommen Meike und ihr Vater wieder von dem Hochsitz herunter.
Zu Hause angekommen, sind alle ein wenig erschöpft und legen sich gemeinsam in ihrem Wohnzimmer auf das riesig große Sofa.
Parallele Linien
Hier siehst du noch einmal, was Geraden und Strecken sind.

- Eine Gerade oder auch Linie (ganz oben) hat keinen Anfangs- und keinen Endpunkt.
- Eine Halbgerade (in der Mitte) hat einen Anfangs-, aber keinen Endpunkt.
- Eine Strecke (ganz unten) hat einen Anfangs- und einen Endpunkt.
Linien können parallel zueinander sein. Parallele Linien schneiden sich nie. Kennst du Beispiele für parallele Linien? Richtig: Die Gleise, auf denen Eisenbahnen fahren, sind parallel zueinander.
Wenn Linien nicht parallel zueinander sind, dann schneiden sie sich an irgendeinem Punkt. Der Punkt, in dem sie sich schneiden, ist der Schnittpunkt. Die Linien schneiden sich dann in einem gewissen Winkel, dem Schnittwinkel.
Senkrechte Linien
Manchmal schneiden sich Linien auf eine besondere Art. Hier siehst du drei Linien, eine rote, eine grüne und eine blaue.
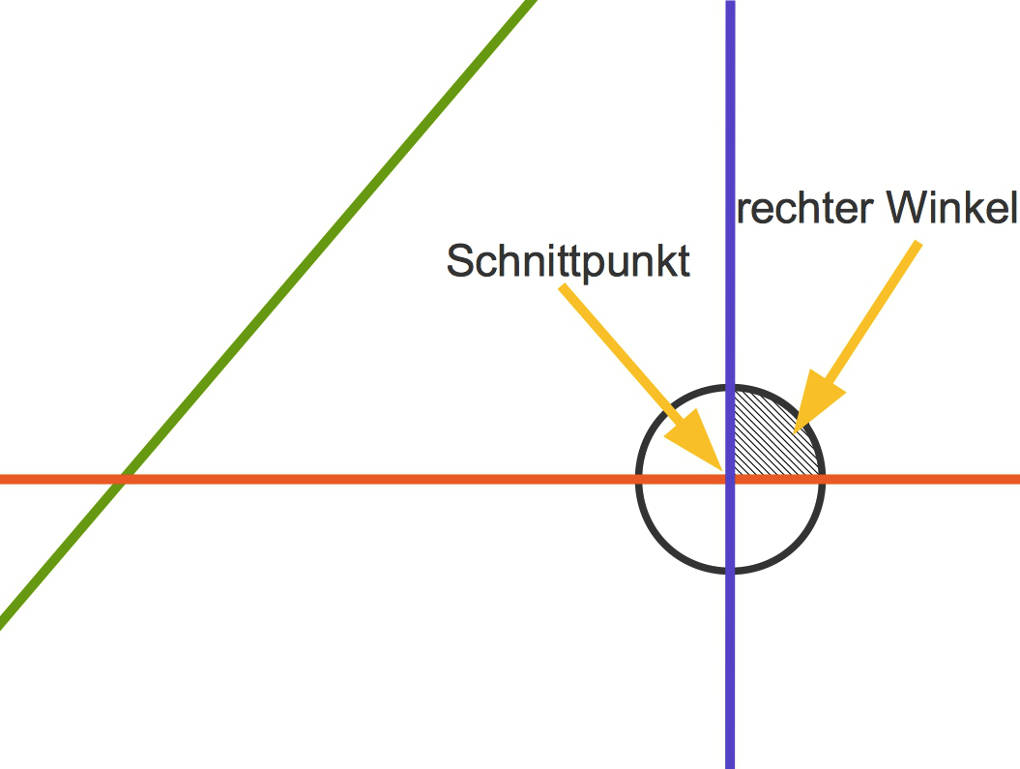
Die grüne Linie und auch die blaue Linie schneiden die rote Linie. Die blaue Linie schneidet die rote Linie senkrecht. Manchmal sagt man auch lotrecht.
Bei senkrechten Linien ist der Schnittwinkel ein rechter Winkel. Daher kommt auch der Name. Ein rechter Winkel beträgt $90^\circ$.
Arbeit mit dem Geodreieck
Das Geodreieck ist ein sehr nützliches Hilfsmittel für die Geometrie. Wie der Name schon sagt, hat es die Form eines Dreiecks. Auf diesem Dreieck gibt es viele hilfreiche Markierungen, wie du auf dieser Abbildung sehen kannst:
Mit Hilfe des Geodreiecks kannst du parallele und senkrechte Linien zu zeichnen.
- Konstruktion einer Parallelen mit Geodreieck:
- Konstruktion einer Senkrechten mit Geodreieck:
Es hilft dir aber auch dabei, Längen und Winkel zu messen. Probiere es am besten einfach mal aus!
Alle Videos zum Thema
Videos zum Thema
Arbeiten mit dem Geodreieck: Geraden, Strecken und Winkel (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Arbeiten mit dem Geodreieck: Geraden, Strecken und Winkel (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal











 Arbeit mit dem Geodreieck
Arbeit mit dem Geodreieck
 Parallele Linien
Parallele Linien
 Senkrechte Linien
Senkrechte Linien












