Lösungsmöglichkeiten quadratischer Gleichungen – Zusammenfassung
Hast du schon einmal von der p-q-Formel gehört? Diese verwendest du, um eine quadratische Gleichung zu lösen. Es gibt aber auch Beispiele von quadratischen Gleichungen, in welchen du diese Formel nicht benötigst.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine quadratische Gleichung?
- Lösen von quadratischen Gleichungen
- Quadratische Gleichungen in allgemeiner Form
- Quadratische Gleichungen in Normalform
- Quadratische Gleichungen in reinquadratischer Form
- Quadratische Gleichungen in der Produktform
- Flächenberechnung mit quadratischen Gleichungen
- Wie viele Lösungen kann eine quadratische Gleichung besitzen?
Was ist eine quadratische Gleichung?
In einer quadratischen Gleichung ist der höchste Exponent der Variable (meist $x$) eine $2$ (also $x^{2}$). Man spricht dies entweder als „$x$ hoch $2$“ oder als „$x$ zum Quadrat“ aus.
Verschiedene Formen quadratischer Gleichungen
Die allgemeine Form einer quadratischen Gleichung lautet $ax^{2}+bx+c=0$. Dabei muss $a\neq 0$ sein.
Abhängig von den Werten der Variablen $a$, $b$ und $c$ kann man nun verschiedene Formen quadratischer Gleichungen unterscheiden.
Eine quadratische Gleichung mit $a=1$ wird Normalform genannt. Durch Umbenennung der Variablen $b$ und $c$ wird diese Form oft so angegeben:
$x^{2}+px+q=0$.
Hier siehst du weitere Spezialfälle:
- Wenn $b=0$ ist lautet die quadratische Gleichung $ax^{2}+c=0$. Eine solche Gleichung wird reinquadratisch genannt.
- Wenn $c=0$ ist lautet die quadratische Gleichung $ax^{2}+bx=0$.
Eine weitere Möglichkeit eine quadratische Gleichung anzugeben, ist die Produktform. Bei dieser lautet die Gleichung $(x-d)\cdot (x-e)=0$.
Welche Lösungswege für quadratische Gleichungen gibt es? Je nachdem, in welcher Form eine quadratische Gleichung gegeben ist, gibt es verschiedene Lösungswege, um diese zu lösen.
Lösen von quadratischen Gleichungen
Quadratische Gleichungen in allgemeiner Form
Um eine quadratische Gleichung in allgemeiner Form $(ax^{2}+bx+c=0)$ zu lösen, verwendest du die Mitternachtsformel (auch abc-Formel genannt):
$x_{1, 2}=\frac{-b \pm \sqrt{b^{2}-4ac}}{2a}$.
Du kannst nun die entsprechenden Werte für $a$, $b$ sowie $c$ einsetzen.
Beispiel 1: $2x^{2}-4x-6=0$
Hier ist $a=2$, $b=-4$ und $c=-6$. Achte unbedingt auf die Vorzeichen. Du erhältst dann die folgenden Lösungen:
$\begin{array}{rcl} x_{1,2}&=&\frac{-(-4) \pm \sqrt{(-4)^{2}-4\cdot 2\cdot (-6)}}{2\cdot 2}\\ &=&\frac{4\pm\sqrt{64}}{4}\\ x_1&=&\frac{4+\sqrt{64}}{4}=\frac{12}4=3\\ x_2&=&\frac{4-\sqrt{64}}{4}=\frac{-4}4=-1 \end{array}$
Quadratische Gleichungen in Normalform
Wenn die quadratische Gleichung in Normalform $x^{2}+px+q=0$ gegeben ist, kannst du die p-q-Formel anwenden:
$x_{1,2}=-\frac p2\pm\sqrt{\left(\frac p2\right)^{2}-q}$.
Beispiel 2: $x^{2}-2x-3=0$
Diese Gleichung erhältst du, wenn du die Gleichung aus Beispiel 1 durch $2$ teilst. Dann ist $p=-2$ und $q=-3$.
$\begin{array}{rcl} x_{1,2}&=&-\frac{-2}2 \pm \sqrt{\left(\frac{-2}2\right)^2-(-3)}\\ &=&1\pm\sqrt{1+3}\\ x_1&=&1+\sqrt{4}=1+2=3\\ x_2&=&1-\sqrt{4}=1-2=-1 \end{array}$
Wie du siehst, erhältst du die gleichen Lösungen wie bei der Mitternachtsformel.
Quadratische Gleichungen in reinquadratischer Form
Eine reinquadratische Gleichung hat die Form $ax^{2}+c=0$. Wie du vorgehst, um eine solche Gleichung zu lösen, siehst du bei dem folgenden Beispiel:
Beispiel 3: $2x^{2}-8=0$
- Addiere auf beiden Seiten $8$. Du erhältst $2x^{2}=8$.
- Dividiere nun durch $2$. Das führt zu $x^{2}=4$.
- Schließlich kannst du die Wurzel ziehen. Denke daran, dass auch das Quadrieren einer negativen Zahl zu einem positiven Ergebnis führt. Die gesuchten Lösungen sind dann $x_{1} = -\sqrt{4}=-2$ und $x_{2}=\sqrt{4}=2$.
Quadratische Gleichungen in der Produktform
Auch diese Form schauen wir uns an einem Beispiel an. Du sollst die Gleichung $(x+2)\cdot (2x-3)=0$ lösen. Da auf der linken Seite ein Produkt steht gilt:
Entweder ist $x+2=0$ oder $2x-3=0$. Die erste Gleichung führt zu $x_1=-2$ und die zweite zu $x_2=\frac32$.
Flächenberechnung mit quadratischen Gleichungen
Hier siehst du ein Quadrat mit der Seitenlänge $x$ und dem Flächeninhalt $A=x^{2}$. Außerdem siehst du ein Rechteck, bei dem die längere Seite doppelt so lang und die kürzere um $3$ (Längeneinheiten) kürzer ist als die Seite des Quadrates. Wie muss $x$ gewählt werden, damit die beiden Flächen den gleichen Inhalt haben?
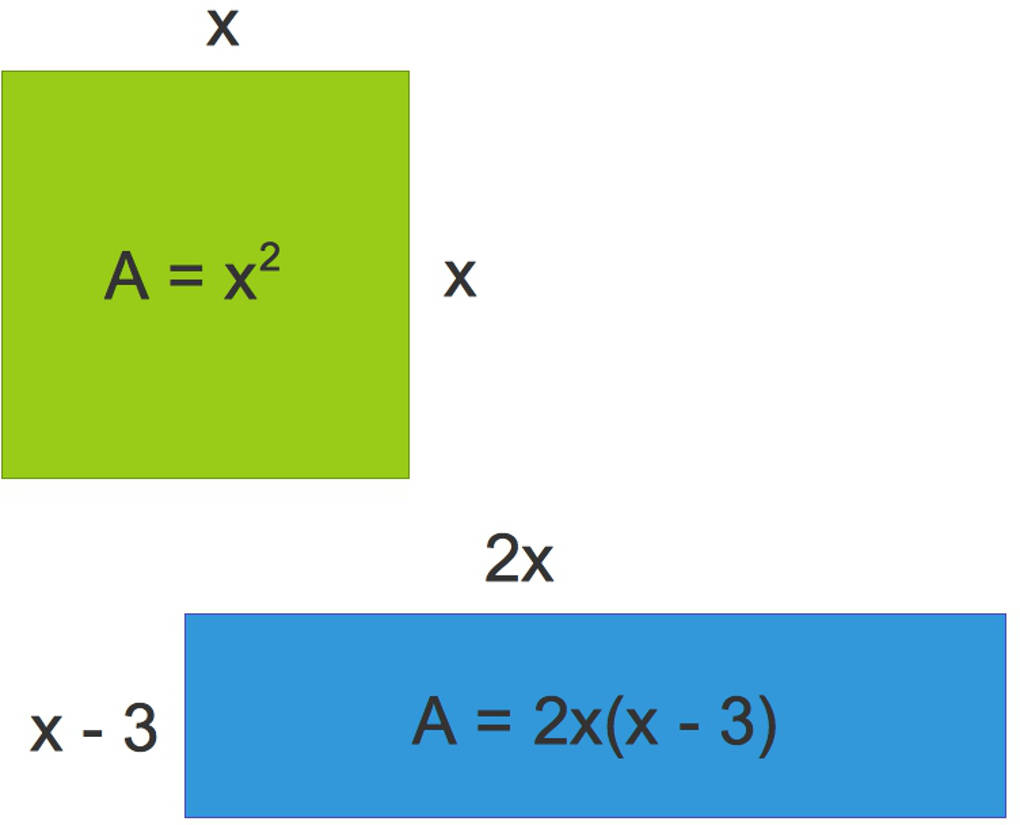
Du musst die Gleichung $2x(x-3)=x^{2}$ lösen:
$\begin{array}{rcll} 2x(x-3) & = & x^{2} & \vert \text{ ausmultiplizieren} \\ 2x^{2}-6x & = & x^{2} & \vert -x^{2} \\ x^{2}-6x & = & 0 & \vert \text{ ausklammern} \\ x(x-6) & = & 0 & \vert \text{ Nullproduktregel} \end{array}$
Das ergibt die Lösungen $x_1=0$ und $x_2=6$. Die erste Lösung ist im Aufgabenkontext nicht sinnvoll. Die Seite des Quadrates ist also $x=6$.
Hier siehst du noch die Probe:
Auf der einen Seite der Gleichung steht $2\cdot 6\cdot(6-3)=12\cdot 3=36$ und auf der anderen $6^{2}=36$. Du hast richtig gerechnet. Super!
Wie viele Lösungen kann eine quadratische Gleichung besitzen?
Hier siehst du einen Überblick über das Lösungsverhalten quadratischer Gleichungen. Dazu kommen wir noch einmal zu der p-q-Formel:
$x_{1,2}=-\frac p2\pm\sqrt{\left(\frac p2\right)^{2}-q}$
Der Term unter der Wurzel $D=\left(\frac p2\right)^{2}-q$ wird Diskriminante genannt. Es gibt drei Fälle:
- Wenn $D>0$ gilt, dann gibt es zwei Lösungen.
- Wenn $D=0$ gilt, dann gibt es nur eine Lösung.
- Wenn $D<0$ gilt, dann gibt es keine Lösung.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Lösungsmöglichkeiten quadratischer Gleichungen – Zusammenfassung (3 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Lösungsmöglichkeiten quadratischer Gleichungen – Zusammenfassung (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter









 Lösungswege für quadratische Gleichungen
Lösungswege für quadratische Gleichungen
 Lösungswege für spezielle quadratische Gleichungen
Lösungswege für spezielle quadratische Gleichungen
 Lösungsverhalten quadratischer Gleichungen – die Diskriminante
Lösungsverhalten quadratischer Gleichungen – die Diskriminante
 Quadratischen Gleichungen – Anwendungsaufgaben
Quadratischen Gleichungen – Anwendungsaufgaben









