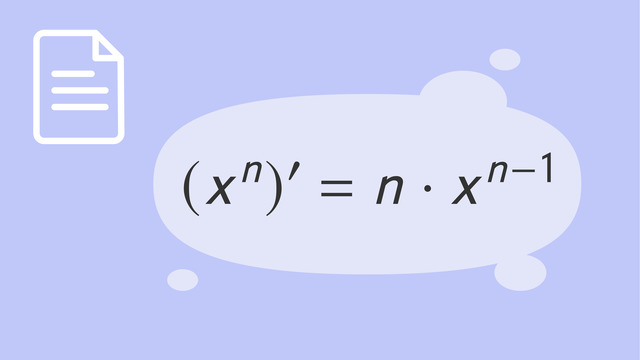Potenzregel bei Brüchen und Wurzeln
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Potenzregel bei Brüchen und Wurzeln
Nach dem Schauen dieses Videos wirst du in der Lage sein, Wurzelfunktionen und gebrochen rationale Funktionen mit der Potenzregel abzuleiten.
Zunächst lernst du, wie man gebrochen rationale Funktionen ableiten kann. Anschließend lernst du, wie man Wurzelfunktionen ableiten kann.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Bruch, Wurzel, Potenzgesetze, Ableitung und Potenzregel.
Bevor du dieses Video schaust, solltest du bereits die Potenzregel für Ableitungen kennen. Außerdem solltest du grundlegendes Wissen zu den Potenzgesetzen haben.
Nach diesem Video wirst du darauf vorbereitet sein, die Produktregel für Ableitungen zu lernen.
Transkript Potenzregel bei Brüchen und Wurzeln
Wenn man über so eine blöde Wurzel stolpert, kann man sich schnell mal 'nen Bruch zuziehen. Da muss man echt höllisch aufpassen! Damit dir ähnliche Unfälle nicht auch noch beim Ableiten zustoßen, schauen wir uns in diesem Video die „Potenzregel bei Brüchen und Wurzeln“ mal ganz genau an! Wie wir eine klassische Potenzfunktion ableiten können, wissen wir ja schon: Den Exponenten als Faktor nach vorne ziehen und um eins verringern. Aber Mathe würde nicht Mathe sein, wenn es das schon gewesen wäre. Natürlich können wir auch Funktionen ableiten, die noch ein bisschen komplizierter aussehen. Fangen wir mal mit einem alten Bekannten an: Einem Bruch. Zum Beispiel „eins durch x Quadrat“ Wie können wir diese Funktion denn jetzt ableiten? Einfach mit der Potenzregel? Dann lautet die Ableitung also „eins durch zwei x“, richtig? Leider nein, leider gar nicht. Aber der Ansatz mit der Potenzregel war grundsätzlich schon genau richtig! Damit wir sie anwenden können, muss aber eine Voraussetzung immer erfüllt sein: Die Potenz, die wir ableiten wollen, muss im Zähler stehen – und nicht im Nenner, wie es hier der Fall ist. Na toll! Und wie genau sollen wir die Potenz jetzt in den Zähler kriegen? Dafür greifen wir einmal ganz tief in die Trickkiste. Denn eine Sache sollte dir, wenn du mit Brüchen rechnest, immer klar sein: „eins durch x Quadrat“ ist nichts anderes als „x hoch minus zwei“. Wir können das x also aus dem Nenner hervorholen, indem wir das Vorzeichen des Exponenten ändern. Vielleicht erinnerst du dich daran, dass du dieses Potenzgesetz mal beim Rechnen mit Potenzen gelernt hast. Vielleicht auch nicht. Spätestens jetzt ist es Zeit, dir diesen Trick zu merken! Denn jetzt haben wir unsere Potenz so umgeformt, dass sie da steht, wo wir sie haben wollen, damit wir sie ableiten können: im Zähler! Und dann können wir die Potenzregel auch tatsächlich anwenden. Das funktioniert jetzt wie gewohnt. Wir ziehen den Exponenten nach vorne und verringern ihn um eins. Achtung, hier gibt es noch eine kleine Stolperfalle: Minus-zwei minus eins ist nicht minus-eins! „Minus-zwei-x hoch minus-drei“ ist also unsere Ableitungsfunktion. Alles klar! Und damit sind jetzt alle happy? Da wäre ich mir nicht zu sicher. Die meisten Mathe-Lehrkräfte stehen drauf, wenn diese Potenz wieder zurück in einen Bruch umgewandelt wird. Dafür wenden wir nochmal den Trick von gerade an, nur andersherum. Wenn im Zähler eine Potenz mit negativem Exponenten steht, können wir diese Potenz wieder nach unten in den Nenner schicken, indem wir das Vorzeichen wieder umdrehen. Dabei nicht den Fehler machen, den Faktor „minus-Zwei“ mitzunehmen. Der bleibt schön da wo er hingehört. Dann haben wir wieder einen Bruch und alle sind glücklich! Nächstes „Fall-Beispiel“: Dieses mal haben wir eine Wurzel gegeben. Und ob du es glaubst oder nicht: Auch diese Funktion können wir mit der Potenzregel ableiten. Allerdings brauchen auch Wurzeln zuvor eine ganz spezielle Behandlung. Keine Sorge! Die ist längst nicht so schlimm wie beim Zahnarzt. An dieser Stelle müssen wir nur wissen, dass wir „Wurzel aus x“ auch schreiben können als „x hoch ein halb“. Dafür haben wir dieses Potenzgesetz angewendet. „Wurzel aus x“ ist ja die Kurzschreibweise für „Zweite Wurzel aus x hoch eins“. Jetzt können wir wieder die Potenzregel auf unsere Funktion loslassen. Die sorgt dafür, dass sich „ein halb“ im Exponenten als Faktor nach vorne zieht und sich der Exponent wieder um eins verringert. Einhalb minus Eins ist Minus-Einhalb. Schon haben wir unsere Ableitung. Aber schön sieht das natürlich nicht aus. Wir räumen also nochmal ein bisschen auf. Uns fällt natürlich sofort auf, dass wir wieder ein Minus im Exponenten haben. Deshalb können wir die Potenz auch in diesem Fall als Bruch schreiben. Jetzt mit positivem Exponenten. Und wie wir „x hoch ein halb“ auch schreiben können, haben wir ja gerade gesehen. Das ist nichts anderes als „Wurzel aus x“. Die beiden Brüche können wir noch zu einem Bruch zusammenfassen und fertig. Ein Meisterwerk! Damit wir uns das Ganze auch merken können, fassen wir nochmal schnell zusammen. Mit der Potenzregel können wir nicht nur ganz normale Potenzfunktionen, sondern auch Brüche und Wurzeln ableiten. Die sind aber etwas speziell und brauchen daher zunächst eine Spezialbehandlung. Wir müssen sie nämlich als Potenz umschreiben. Denn dann können wir die Potenzregel ohne Probleme anwenden. Anschließend können wir die entsprechende Ableitung dann wieder als Bruch, oder gegebenenfalls auch wieder als Wurzel schreiben. Mit dieser Vorgehensweise haben wir die Wurzeln fest im Griff und müssen so schnell auch keine Brüche mehr fürchten!
Potenzregel bei Brüchen und Wurzeln Übung
-
Vervollständige das Beispiel zur Potenzregel bei Brüchen.
TippsDu kannst die Funktion $g(x)$ ohne Bruch, allerdings mit einem negativen Exponenten schreiben.
Beispiel:
$g(x)=\dfrac{1}{x^3}=x^{-3}$
$ g'(x) = -3 \cdot x^{-4}= -3 \cdot \dfrac{1}{x^4} = -\dfrac{3}{x^4}$
LösungWir können Brüche mithilfe der Potenzregel ableiten. Dazu müssen wir jedoch den Bruch zunächst als Potenz darstellen. Dabei gilt:
$\dfrac{1}{x^n}=x^{-n}$
Wir können dies auf unser Beispiel anwenden. Wir schreiben den Term ohne Bruch, allerdings mit einem negativen Exponenten:
$g(x)=\dfrac{1}{x^2}=x^{-2}$Wir können nun die Potenzregel anwenden:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$
Wir müssen den Exponenten als Faktor vor die Potenz setzen und den Exponenten der Potenz um eins verringern:
$ g'(x)= -2 \cdot x^{-2-1} = -2 \cdot x^{-3}$
Wir können nun den Term wieder als Bruch schreiben:
$ g'(x)= -2 \cdot \dfrac{1}{x^3} = -\dfrac{2}{x^3}$ -
Bestimme die Ableitung der Funktion mithilfe der Potenzregel.
TippsWir können die Potenzregel auch auf Wurzeln anwenden. Dazu müssen wir jedoch die Wurzel als Potenz darstellen:
$\sqrt[n]{x^m}=x^{\frac{m}{n}}$Die Potenzregel lautet allgemein:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$
LösungDie Potenzregel hilft uns, Ableitungen von Potenzen zu bestimmen:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$
Wir können die Potenzregel auch auf Wurzeln anwenden. Dazu müssen wir jedoch die Wurzel zunächst als Potenz darstellen. Dabei gilt:
$\sqrt[n]{x^m}=x^{\frac{m}{n}}$
Wir müssen also den Exponenten als Bruch schreiben. Danach können wir die Potenzregel anwenden und schreiben den Exponenten als Faktor vor die Potenz und verringern den Exponenten der Potenz um eins.Wir wenden dies auf unsere Funktionen an:
Erste Funktion:
$f(x)=\sqrt{x} = x^{\frac{1}{2}}$
$f'(x)= \dfrac{1}{2} \cdot x^{\frac{1}{2}-1} = \dfrac{1}{2} \cdot x^{-\frac{1}{2}}$
Wir können nun den Term wieder als Wurzel schreiben:
$f'(x)= \dfrac{1}{2} \cdot x^{-\frac{1}{2}} = \dfrac{1}{2} \cdot \dfrac{1}{x^{\frac{1}{2}}}= \dfrac{1}{2} \cdot \dfrac{1}{\sqrt{x}} = \dfrac{1}{2\sqrt{x}} $Zweite Funktion:
$f(x)= \sqrt[3]{x^2}=x^{\frac{2}{3}}$
$f'(x)= \dfrac{2}{3} \cdot x^{\frac{2}{3}-1} = \dfrac{2}{3} \cdot x^{-\frac{1}{3}}$
Wir können nun den Term wieder als Wurzel schreiben:
$f'(x)= \dfrac{2}{3} \cdot x^{-\frac{1}{3}}= \dfrac{2}{3} \cdot \dfrac{1}{x^{\frac{1}{3}}}= \dfrac{2}{3} \cdot \dfrac{1}{\sqrt[3]{x}} = \dfrac{2}{3\sqrt[3]{x}} $Dritte Funktion:
$f(x)= \sqrt[3]{x}=x^{\frac{1}{3}}$
$f'(x)= \dfrac{1}{3} \cdot x^{\frac{1}{3}-1} = \dfrac{1}{3} \cdot x^{-\frac{2}{3}}$
Wir können nun den Term wieder als Wurzel schreiben:
$f'(x)= \dfrac{1}{3} \cdot x^{-\frac{2}{3}}= \dfrac{1}{3} \cdot \dfrac{1}{x^{\frac{2}{3}}}= \dfrac{1}{3} \cdot \dfrac{1}{\sqrt[3]{x^2}} = \dfrac{1}{3\sqrt[3]{x^2}} $Vierte Funktion:
$f(x)=2\sqrt{x} = 2x^{\frac{1}{2}}$
$f'(x)= 2 \cdot \dfrac{1}{2} \cdot x^{\frac{1}{2}-1} = 2 \cdot \dfrac{1}{2} \cdot x^{-\frac{1}{2}}$
Wir können nun den Term wieder als Wurzel schreiben:
$f'(x)= 2 \cdot \dfrac{1}{2} \cdot x^{-\frac{1}{2}} = \dfrac{1}{x^{\frac{1}{2}}}= \dfrac{1}{\sqrt{x}} $ -
Ermittle die Ableitungen der gegebenen Funktionen.
TippsWir können Brüche und Wurzeln mihilfe der Potenzregel ableiten:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$Wurzeln können zu Potenzen umgewandelt werden.
Beispiel:
$\sqrt{x^3}=x^{\frac{3}{2}}$
$\sqrt[3]{x^2}=x^{\frac{2}{3}}$LösungWir können Brüche und Wurzeln mithilfe der Potenzregel ableiten:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$Dazu müssen wir diese jedoch zunächst als Potenz darstellen. Dabei gilt:
- $\dfrac{1}{x^n}=x^{-n}$
- $\sqrt[n]{x^m}=x^{\frac{m}{n}}$
Wir schreiben die gegebenen Funktionen also zunächst als Potenz und leiten diese dann ab:
Aufgabe 1:
$f(x)= \sqrt{x^3}=x^{\frac{3}{2}}$
$f'(x)= \dfrac{3}{2} \cdot x^{\frac{3}{2}-1} = \dfrac{3}{2} \cdot x^{\frac{1}{2}}= \dfrac{3}{2} \cdot \sqrt{x}= \dfrac{3\sqrt {x}}{2} $Aufgabe 2:
$g(x)=\dfrac{3}{x^3}=3x^{-3}$
$g'(x)= 3 \cdot (-3) \cdot x^{-3-1} = -9 \cdot x^{-4} = -9 \cdot \dfrac{1}{x^4} = -\dfrac{9}{x^4}$Aufgabe 3:
$h(x)=\dfrac{1}{2x^3}=\dfrac{1}{2} x^{-3}$$h'(x)= \dfrac{1}{2} \cdot (-3) \cdot x^{-3-1} = -\dfrac{3}{2} \cdot x^{-4} = -\dfrac{3}{2} \cdot \dfrac{1}{x^4} = -\dfrac{3}{2x^4}$
Aufgabe 4:
$i(x)= \sqrt[3]{x^5}=x^{\frac{5}{3}}$
$i'(x)= \dfrac{5}{3} \cdot x^{\frac{5}{3}-1} = \dfrac{5}{3} \cdot x^{\frac{2}{3}}= \dfrac{5}{3} \cdot \sqrt[3]{x^2}= \dfrac{5 \sqrt[3]{x^2}}{3} $ -
Überprüfe die Ableitungen.
TippsSchreibe die Funktion zunächst als Potenz. Bilde dann die Ableitung mithilfe der Potenzregel und vergleiche mit der gegebenen Ableitung.
Achte auf die Vorzeichen!
LösungUm zu überprüfen, ob die Ableitungen richtig gebildet wurden, müssen wir die Potenzregel anwenden:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$Dazu müssen wir die Funktionen jedoch zunächst als Potenz darstellen. Dabei gilt:
- $\dfrac{1}{x^n}=x^{-n}$
- $\sqrt[n]{x^m}=x^{\frac{m}{n}}$
Wir schreiben die gegebenen Funktionen also zunächst als Potenz und überprüfen dann die Ableitung:
Funktion 1:
$\color{#669900}{f(x)= 3\sqrt{x^5} \quad f'(x)= \dfrac{15\sqrt {x^3}}{2}}$
Richtig! Wir rechnen Schritt für Schritt nach:
$f(x)= 3\sqrt{x^5}=3x^{\frac{5}{2}}$
$f'(x)= 3 \cdot \dfrac{5}{2} \cdot x^{\frac{5}{2}-1} = \dfrac{15}{2} \cdot x^{\frac{3}{2}}= \dfrac{15}{2} \cdot \sqrt{x^3}= \dfrac{15\sqrt {x^3}}{2} $Funktion 2:
$f(x)=\dfrac{4}{x^4} \quad f'(x)= -\dfrac{4}{x^5}$
Falsch! Ein Faktor $4$ wurde vergessen. Richtig lautet die Rechnung:
$f(x)=\dfrac{4}{x^4}=4x^{-4}$$f'(x)= 4 \cdot ({-}4) \cdot x^{-4-1} = -16 \cdot x^{-5} = -16 \cdot \dfrac{1}{x^5} = -\dfrac{16}{x^5}$
Funktion 3:
$f(x)=-\dfrac{3}{2x^3} \quad f'(x) =- \dfrac{9}{2x^4}$
Falsch! Hier wurde ein Vorzeichenfehler gemacht. Richtig lautet die Rechnung:
$f(x)=-\dfrac{3}{2x^3}=-\dfrac{3}{2} x^{-3}$$f'(x)= -\dfrac{3}{2} \cdot ({-}3) \cdot x^{-3-1} = \dfrac{9}{2} \cdot x^{-4} = \dfrac{9}{2} \cdot \dfrac{1}{x^4} = \dfrac{9}{2x^4}$
Funktion 4:
$\color{#669900}{f(x)= \sqrt[5]{x^3} \quad f'(x)= \dfrac{3}{5\sqrt[5]{x^3}}}$
Richtig! Wir rechnen Schritt für Schritt nach:
$f(x)= \sqrt[5]{x^3}=x^{\frac{3}{5}}$$f'(x)= \dfrac{3}{5} \cdot x^{\frac{3}{5}-1} = \dfrac{3}{5} \cdot x^{-\frac{2}{5}}= \dfrac{3}{5} \cdot \dfrac{1}{x^{\frac{2}{5}}}= \dfrac{3}{5} \cdot \dfrac{1}{\sqrt[5]{x^2}} = \dfrac{3}{5\sqrt[5]{x^2}} $
-
Stelle die Brüche und Wurzeln als Potenzen dar.
TippsEntscheide zunächst, ob du eine Wurzel oder einen Bruch vorliegen hast. Je nachdem ändert sich die Umformung zu einer Potenz.
Liegt ein Bruch vor, schreibst du den Term ohne Bruch, allerdings mit einem negativen Exponenten.
Beispiel:
$g(x)=\dfrac{1}{x^4}=x^{-4}$
LösungDie Potenzregel hilft uns, Ableitungen von Potenzen zu bestimmen:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$
Wir können auch Brüche und Wurzeln mithilfe der Potenzregel ableiten. Dazu müssen wir diese jedoch zunächst als Potenz darstellen. Und zwar so, dass die Potenz im Zähler steht. Dazu verwenden wir folgende Zusammenhänge:- Für Wurzeln gilt: $\sqrt[n]{x^m}=x^{\frac{m}{n}}$
- Für Brüche gilt: $\dfrac{1}{x^n}=x^{-n}$
- $\sqrt{x} = \sqrt[2]{x^1} = x^{\frac{1}{2}}$
- $\sqrt[3]{x^2}=x^{\frac{2}{3}}$
- $\dfrac{1}{x^2}=x^{-2}$
- $\dfrac{1}{x^1}=x^{-1}$
-
Bestimme die zweite Ableitung der Funktionen.
TippsWir können die zweite Ableitung bestimmen, indem wir die erste Ableitung erneut ableiten.
Lass die erste Ableitung als Potenz stehen, um die zweite Ableitung zu bilden.
LösungWir können Brüche und Wurzeln ableiten, indem wir sie zunächst als Potenz darstellen:
- $\dfrac{1}{x^n}=x^{-n}$
- $\sqrt[n]{x^m}=x^{\frac{m}{n}}$
Anschließend können wir sie mithilfe der Potenzregel ableiten:
$f(x)= x^n \quad f'(x)= n \cdot x^{n-1}$Wir können die zweite Ableitung bestimmen, indem wir die erste Ableitung erneut ableiten. Damit ergibt sich:
Aufgabe 1:
$f_1(x)=\dfrac{3}{4x^5}=\dfrac{3}{4} x^{-5}$$f_1^\prime(x)= \dfrac{3}{4} \cdot ({-}5) \cdot x^{-5-1} = -\dfrac{15}{4} \cdot x^{-6} $
$f_1^{\prime\prime}(x)= {-}\dfrac{15}{4} \cdot ({-}6) \cdot x^{-6-1} =\dfrac{90}{4} \cdot x^{-7} = \dfrac{90}{4x^7} = \dfrac{45}{2x^7}$
Aufgabe 2:
$f_2(x)= \dfrac{4}{3} \sqrt[4]{x^3}=\dfrac{4}{3} x^{\frac{3}{4}}$$f_2^\prime(x)= \dfrac{4}{3} \cdot \dfrac{3}{4} \cdot x^{\frac{3}{4}-1} = x^{-\frac{1}{4}}$
$f_2^{\prime\prime}(x)= {-}\dfrac{1}{4} \cdot x^{-\frac{1}{4}-1} = - \dfrac{1}{4} \cdot x^{-\frac{5}{4}} = {-}\dfrac{1}{4 \sqrt[4]{x^5}}$
8.883
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.852
Lernvideos
37.617
Übungen
33.734
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Exponentialfunktion Beispiel
