Satz von Bayes

Inhaltsverzeichnis zum Thema

• Bedingte Wahrscheinlichkeiten
• Der Multiplikationssatz sowie der Satz von der totalen Wahrscheinlichkeit
• Der Multiplikationssatz
• Der Satz von der totalen Wahrscheinlichkeit
• Der Satz von Bayes

Bedingte Wahrscheinlichkeiten

Wenn bei einem mehrstufigen Zufallsexperiment der Ausgang in einer Stufe von dem Ausgang der vorherigen Stufe abhängt, spricht man von bedingten Wahrscheinlichkeiten.

Schau dir hierfür ein Beispiel an: Meike zieht zunächst aus einer Urne mit $3$ roten und $2$ grünen Kugeln eine Kugel. Je nachdem, welche Farbe die Kugel hat, nimmt sie nun einen roten oder einen grünen Würfel mit den hier abgebildeten Netzen her.

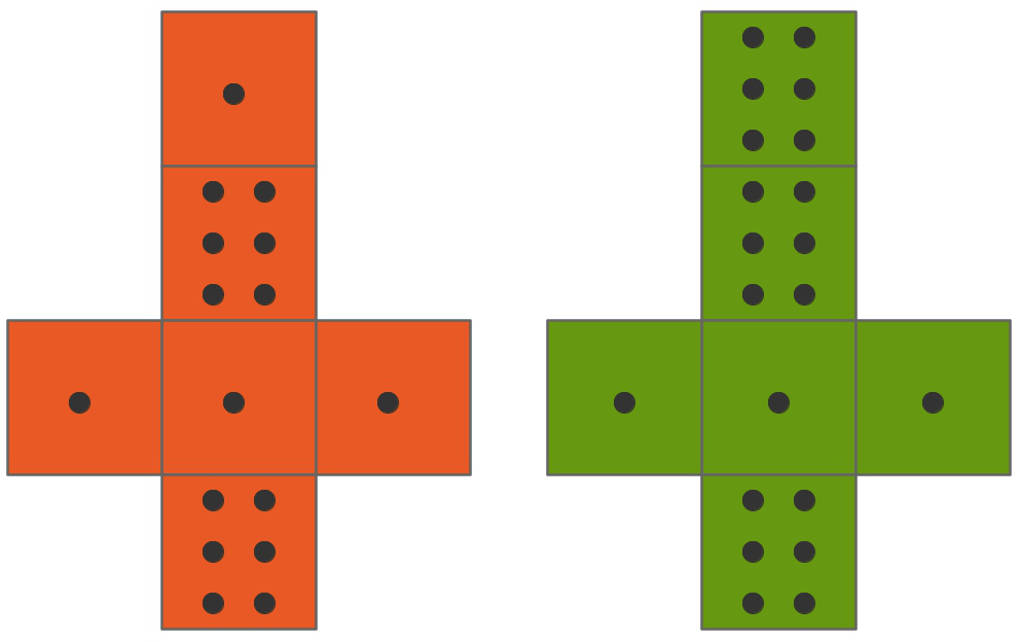
Du siehst, dass die Wahrscheinlichkeit, eine $6$ zu würfeln, bei den beiden Würfeln verschieden groß ist.

Zunächst schauen wir uns einmal etwas genauer an, was eine bedingte Wahrscheinlichkeit ist:

• Die Wahrscheinlichkeit, eine $6$ zu würfeln, unter der Bedingung, dass Meike eine rote ($\text{R}$) Kugel gezogen hat, beträgt $\frac13$. Dies schreibt man so $P_{\text{R}}(6)=\frac13$ oder auch $P(6|\text{R})=\frac13$.
• Ebenso kannst du die Wahrscheinlichkeit dafür angeben, dass Meike eine $6$ würfelt, nachdem sie eine grüne Kugel ($\text{G}$) gezogen hat: $P_{\text{G}}(6)=\frac12$ oder auch $P(6|\text{G})=\frac12$.

Das betrachtete zweistufige Zufallsexperiment kannst du mit Hilfe eines Baumdiagramms darstellen:

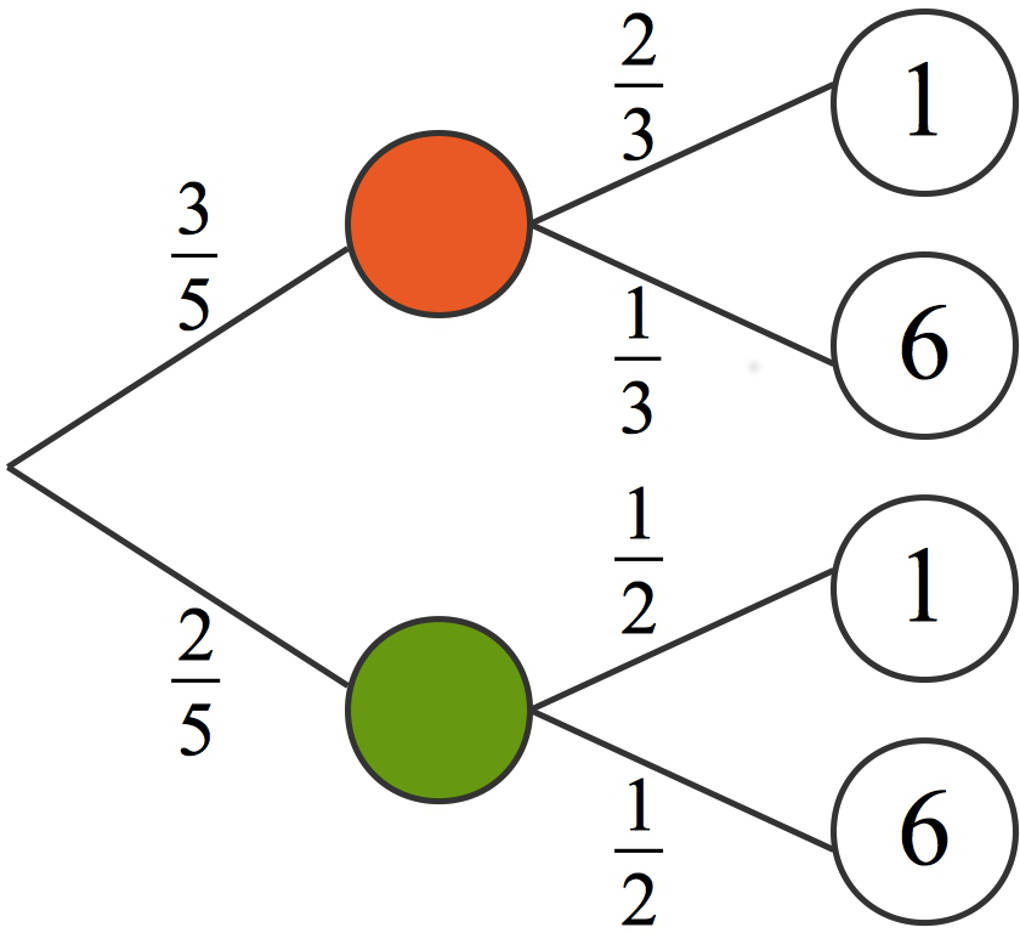
Wir berechnen nun Schritt für Schritt die Wahrscheinlichkeit dafür, dass Meike eine $6$ würfelt.

Der Multiplikationssatz sowie der Satz von der totalen Wahrscheinlichkeit

Es gibt zwei Pfade, welche zu einer $6$ führen. Um die jeweilige Wahrscheinlichkeit zu berechnen, verwendest du die 1. Pfadregel oder auch die Produktregel.

Der Multiplikationssatz

Im Zusammenhang mit bedingten Wahrscheinlichkeiten spricht man von dem Multiplikationssatz:

• $P(\text{R}\cap 6)=\frac35\cdot \frac13=\frac15$
• $P(\text{G}\cap 6)=\frac25\cdot \frac12=\frac15$

Der Satz von der totalen Wahrscheinlichkeit

Da nun zwei Pfade zu der $6$ führen, müssen die entsprechenden Wahrscheinlichkeiten addiert werden. $P(6)=P(\text{R}\cap 6)+P(\text{G}\cap 6)=\frac15+\frac15=\frac25$. Dies ist der Satz von der totalen Wahrscheinlichkeit.

Nun kommt Meikes Freund Paul und sieht, dass Meike eine $6$ gewürfelt hat. Paul möchte nun wissen, wie groß die Wahrscheinlichkeit dafür ist, dass Meike im ersten Durchgang eine rote Kugel gezogen hat. Gut, er könnte sich die Farbe des Würfels anschauen, aber nehmen wir doch einmal an, dass der Würfel für die zweite Stufe in einer roten oder einer grünen Kiste gelegen hat und nicht mehr die Farbe der Kiste zu erkennen ist.

Paul möchte also die folgende bedingte Wahrscheinlichkeit wissen: $P_{6}(\text{R})$ oder $P(\text{R}|6)$. Die Bedingung oder das, was du weißt, ist nun nicht mehr die Farbe der Kugel, sondern die geworfene Augenzahl.

Hier hilft dir der Satz von Bayes weiter.

Der Satz von Bayes

Wir fassen noch einmal den Multiplikationssatz und auch den Satz von der totalen Wahrscheinlichkeit etwas allgemeiner zusammen. Dabei betrachten wir das hier abgebildete Baumdiagramm:

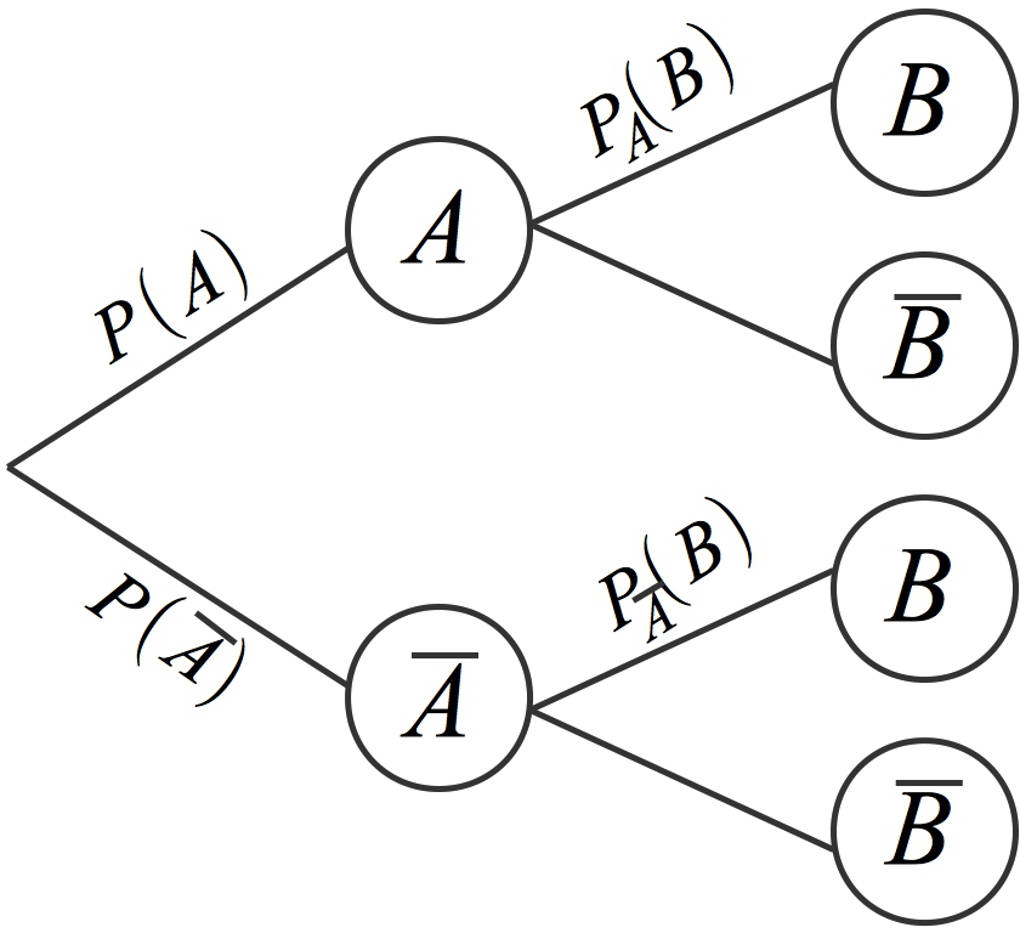
• Der Multiplikationssatz: $P(A\cap B)=P(A)\cdot P_{A}(B)$
• Der Satz von der totalen Wahrscheinlichkeit: $P(B)=P(A)\cdot P_{A}(B)+P(\overline{A})\cdot P_{\overline{A}}(B)$.

Der Satz von Bayes zur Berechnung der Wahrscheinlichkeit $P_{B}(A)$:

$P_{B}(A)=\frac{P(A\cap B)}{P(B)}=\frac{P(A)\cdot P_{A}(B)}{P(A)\cdot P_{A}(B)+P(\overline{A})\cdot P_{\overline{A}}(B)}$

Das sieht sehr kompliziert aus. Du kannst allerdings vielleicht bereits erkennen, dass im Zähler das Ergebnis aus dem Multiplikationssatz und im Nenner das aus dem Satz von der totalen Wahrscheinlichkeit steht.

Nun kommen wir wieder zu Paul zurück, dessen Frage ja noch nicht beantwortet ist. Meike rechnet ihm das nun vor. Sie verwendet den Satz von Bayes:

$P_{6}(\text{R})=\frac{P(\text{R}\cap 6)}{P(\text{R}\cap 6)+P(\text{G}\cap 6)}=\frac{\frac15}{\frac25}=\frac12$