Addition und Subtraktion: Halbschriftlich und schriftlich
Beim schriftlichen Subtrahieren werden Minuend und Subtrahend in einer Stellenwerttafel untereinander geschrieben. Halbschriftlich subtrahieren in der Mathematik ist ein Verfahren, um mit etwas größeren Zahlen zu rechnen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist Addition?
- Wie addierst du schriftlich?
- Schriftliches Addieren ohne Übertrag
- Schriftliches Addieren mit Übertrag
- Schriftliches Addieren mehrerer Zahlen
- Wie addierst du halbschriftlich?
- Der Zusammenhang zwischen Addition und Subtraktion
- Halbschriftliches Subtrahieren
- Schriftliches Subtrahieren
Was ist Addition?
Die Addition ist eine der vier Grundrechenarten. Wenn du zu der 5 die 3 dazutust, erhältst du 8. Das nennt man Addieren. Wir schreiben 5+3=8:
- Das „+“-Zeichen sagt uns, dass wir 5 und 3 addieren müssen.
- 5 und 3 sind die Summanden.
- Das Ergebnis 8 wird Summe genannt.
Wofür benötigst du eigentlich die Addition? Wenn du an deinem Geburtstag von deinen Eltern, von deiner Tante und von deinem Opa jeweils etwas Geld geschenkt bekommst, möchtest du natürlich wissen, wie viel Geld du nun insgesamt hast. Du zählst also die einzelnen Beträge zusammen: Du addierst sie. Diese Addition wird schon recht kompliziert, wenn die Zahlen etwas größer werden. Dann hilft dir zum Beispiel eine Stellenwerttafel weiter.
Wie addierst du schriftlich?
Schriftliches Addieren ohne Übertrag
Wenn du 234 und 12 schriftlich addieren möchtest, kannst du dies so machen:
- Du trägst den ersten Summanden 234 in die erste Zeile einer Stellenwerttafel ein. Die 2 schreibst du an die Hunderterstelle, die 3 an die Zehner- und die 4 an Einerstelle.
- Nun schreibst du in die Zeile darunter stellengenau den anderen Summanden 12: Die 1 an die Zehnerstelle und die 2 an die Einerstelle.
- Vor die untere Zahl schreibst du ganz links ein Pluszeichen. Damit ist klar, dass du addierst.
- Nun addierst du von rechts nach links: Erst die Einer, dann die Zehner und zuletzt die Hunderter.
- Da der zweite Summand keine Hunderterstelle hat, kannst du dir hier eine Null dazu denken.
Die gesamte schriftliche Addition sieht dann so aus:
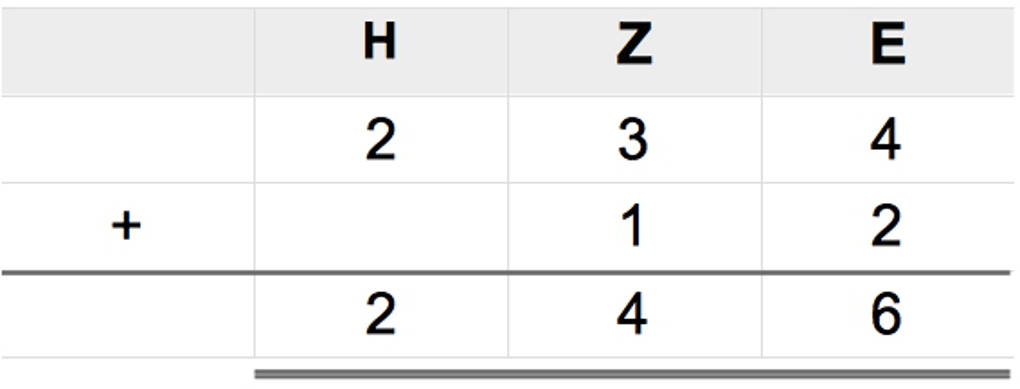
Du kannst schreiben: 234+12=246.
Schriftliches Addieren mit Übertrag
Wir schauen uns ein weiteres Beispiel an. Dieses Mal musst du einen Übertrag machen.
Paul liebt vegane Gummibärchen! Seine Schwester hilft ihm dabei, seine Gummibärchen zu zählen. Beide zählen jeweils einen Haufen Gummibärchen: Pauls Schwester zählt 156 Gummibärchen und Paul 77. Wie viele sind das nun zusammen? Du hast es sicher gemerkt: Die beiden müssen die Zahlen addieren:
Sie schreiben erst einmal die jeweiligen Zahlen in eine Stellenwerttafel, so wie sie es in der Schule gelernt haben:
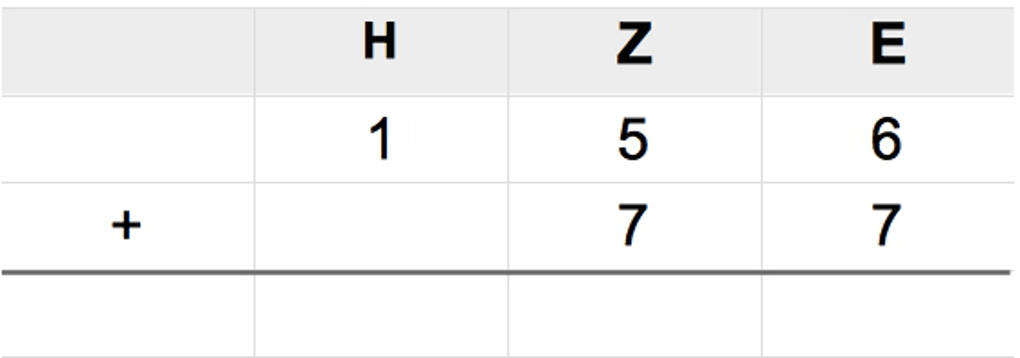
Zuerst addieren sie die Einer. Nanu! Was ist hier passiert? 6+7 ist 13 und sie dürfen doch nur eine Stelle im Einerfeld eintragen. Sie schreiben die 3 an die Einerstelle des Ergebnisses und die 1 schreiben sie als Übertrag an die Zehnerstelle. Die 1 als Übertrag kannst du erkennen, da sie grün und etwas kleiner geschrieben ist.
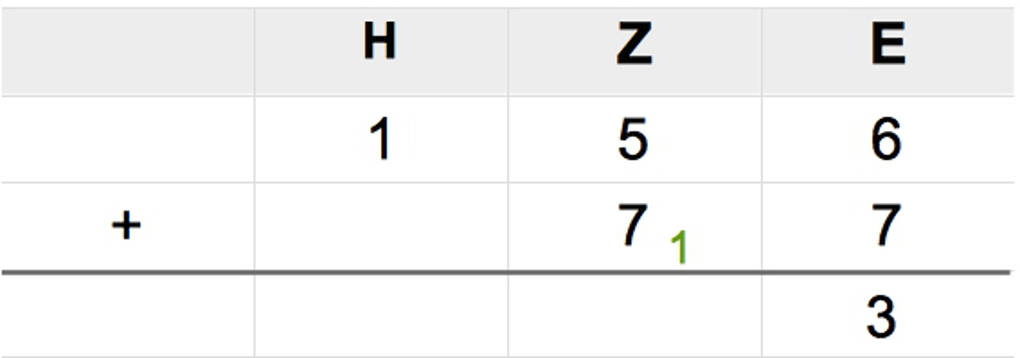
Wenn die beiden jetzt die Zehner addieren, dürfen sie den Übertrag nicht vergessen: 1+7+5=13. Sie müssen wieder einen Übertrag machen. Die 3 können sie schon an die Zehnerposition des Ergebnisses schreiben. Der Übertrag gehört nun an die Hunderterstelle.
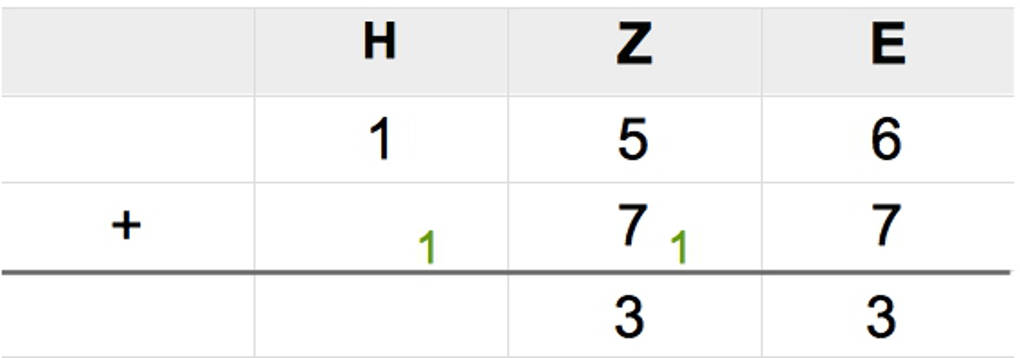
Nun können sie noch zu der 1 von dem ersten Summanden den Übertrag 1 addieren und erhalten die 2 an der Hunderterstelle des Ergebnisses.
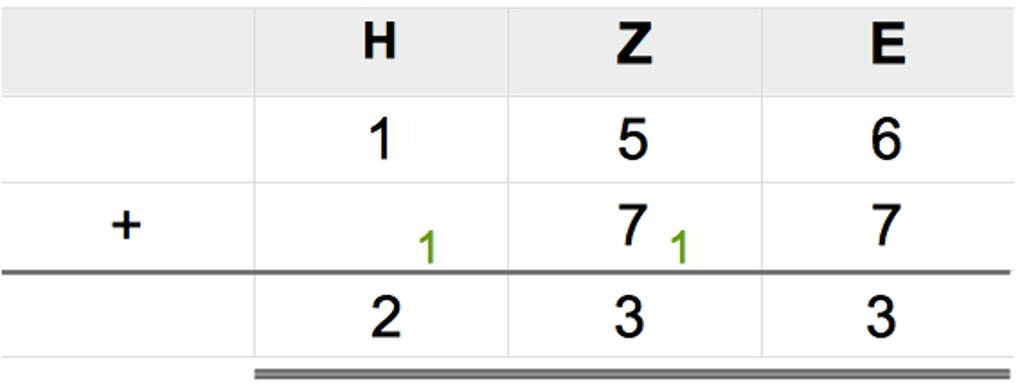
Das Ergebnis unterstreichen sie: Insgesamt hat Paul 233 Gummibärchen. Weil seine Schwester ihm geholfen hat, schenkt er ihr 50 Gummibärchen. Wie viele hat er jetzt noch? Das lernst du ein anderes Mal beim Subtrahieren.
Schriftliches Addieren mehrerer Zahlen
Du sollst die Summe mehrerer Zahlen 222+144+34 berechnen. Du kannst auch hier alle Zahlen zunächst in eine Stellenwerttafel eintragen, genau so wie bei zwei Summanden. Dann addierst du von rechts nach links. Wenn eine Zwischensumme zweistellig ist, musst du einen Übertrag machen.
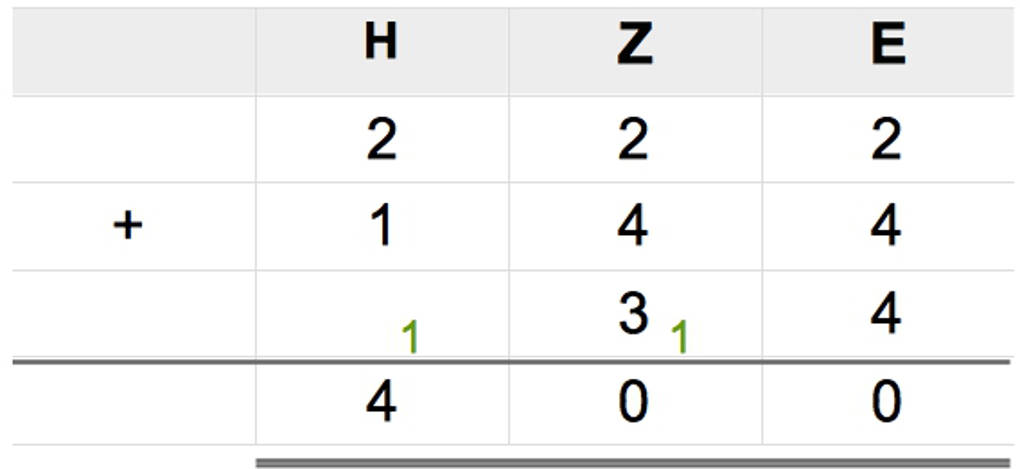
Wie addierst du halbschriftlich?
Beim halbschriftliche Addieren addierst du die Summanden stellenweise und addierst am Schluss die einzelnen Ergebnisse. Wie viele Gummibärchen hatte Paul noch gleich? Er musste 156+77 rechnen:
- Wir addieren zuerst die Hunderter. Da der zweite Summand keine Hunderter hat, sind wir schon fertig: 100.
- Nun addieren wir die Zehner: 50+70=120.
- Bleiben noch die Einer übrig: 6+7=13.
Zuletzt können wir die Zwischenergebnisse addieren: 100+120+13=233.
Wie viele Einwohner haben Berlin und Hamburg gemeinsam?
Vielleicht fragst du dich jetzt, ob du auch schon richtig große Zahlen addieren kannst. Ja, auch das geht, wie du im nächsten Beispiel sehen kannst. Berlin und Hamburg sind die beiden größten Städte Deutschlands:
- Berlin hat 3520031 und
- Hamburg hat 1860759 Einwohner.
Luke soll als Hausaufgabe rechnen, wie viele Einwohner die beiden Städte zusammen haben: Er addiert halbschriftlich:
- die Millionen: 3000000+1000000=4000000
- die Hundertausender: 500000+800000=1300000
- die Zehntausender: 20000+60000=80000
- die Tausender: 0+0=0
- die Hunderter: 0+700=700
- die Zehner: 30+50=80
- die Einer: 1+9=10
Jetzt ist Luke fast fertig. Er muss noch die jeweiligen Zwischensummen addieren:
4000000+1300000+80000+700+80+10=5380790.
Berlin und Hamburg haben also zusammen 5380790 Einwohner. Das ist ja ganz schön viel.
Der Zusammenhang zwischen Addition und Subtraktion
 Die Addition und die Subtraktion hängen sehr eng zusammen. Beide sind Strichrechnungen. Du kennst bereits die Addition. Wenn du zu 30 Schokokäfern 15 dazu tust, wird dies als Addieren bezeichnet. Das Rechenzeichen dazu ist das Plus-Zeichen: $\color{#669900}{+}$. Die Rechnung zu dieser Aufgabe sieht so aus:
Die Addition und die Subtraktion hängen sehr eng zusammen. Beide sind Strichrechnungen. Du kennst bereits die Addition. Wenn du zu 30 Schokokäfern 15 dazu tust, wird dies als Addieren bezeichnet. Das Rechenzeichen dazu ist das Plus-Zeichen: $\color{#669900}{+}$. Die Rechnung zu dieser Aufgabe sieht so aus:
30 + 15 = 45 .
Wenn du nun umgekehrt von diesen 45 Schokokäfern 12 abgibst, möchtest du vielleicht wissen, wie viele du dann noch übrig hast: 45 = 12 +?. Wie findest du heraus, welche Zahl du für das Fragezeichen einsetzen sollst? Dieses mal subtrahierst du 12 von 45. Das Rechenzeichen für die Subtraktion ist das Minus-Zeichen: $\color{#669900}{-}$.
45 -12 = 33
Bezeichnungen
Bei der Grundrechenart Addition werden die einzelnen Teile so benannt:
Summand + Summand = Summe.
Warum heißt sowohl der Term vor als auch der nach dem Plus-Zeichen Summand? Das liegt daran, dass man beim Addieren die Reihenfolge vertauschen darf. Zum Beispiel ist 30 + 15 = 15 + 30 = 45.
Beim Subtrahieren darfst du die Reihenfolge nicht vertauschen. Deshalb haben die Terme vor und nach dem Minus-Zeichen auch verschiedene Bezeichnungen.
Bei der Grundrechenart Subtraktion nennt man die einzelnen Teile so:
Minuend - Subtrahend = Differenz.
Bei der Schokokäfer-Aufgabe 45 - 12 = 33 ist damit
- 45 der Minuend,
- 12 der Subtrahend und
- 33 die Differenz, das Ergebnis der Subtraktion.
Halbschriftliches Subtrahieren
Wenn die Aufgaben etwas komplizierter werden als bei dem Beispiel mit den Schokokäfern, kannst du schriftlich oder halbschriftlich subtrahieren.
Du sollst zum Beispiel Zahlen, die bis zu einer Millionen gehen, subtrahieren. Schau dir die verschiedenen Stellen einer solchen Zahl an: Die Hunderttausender, die Zehntausender, die Tausender, die Hunderter, die Zehner und die Einer.
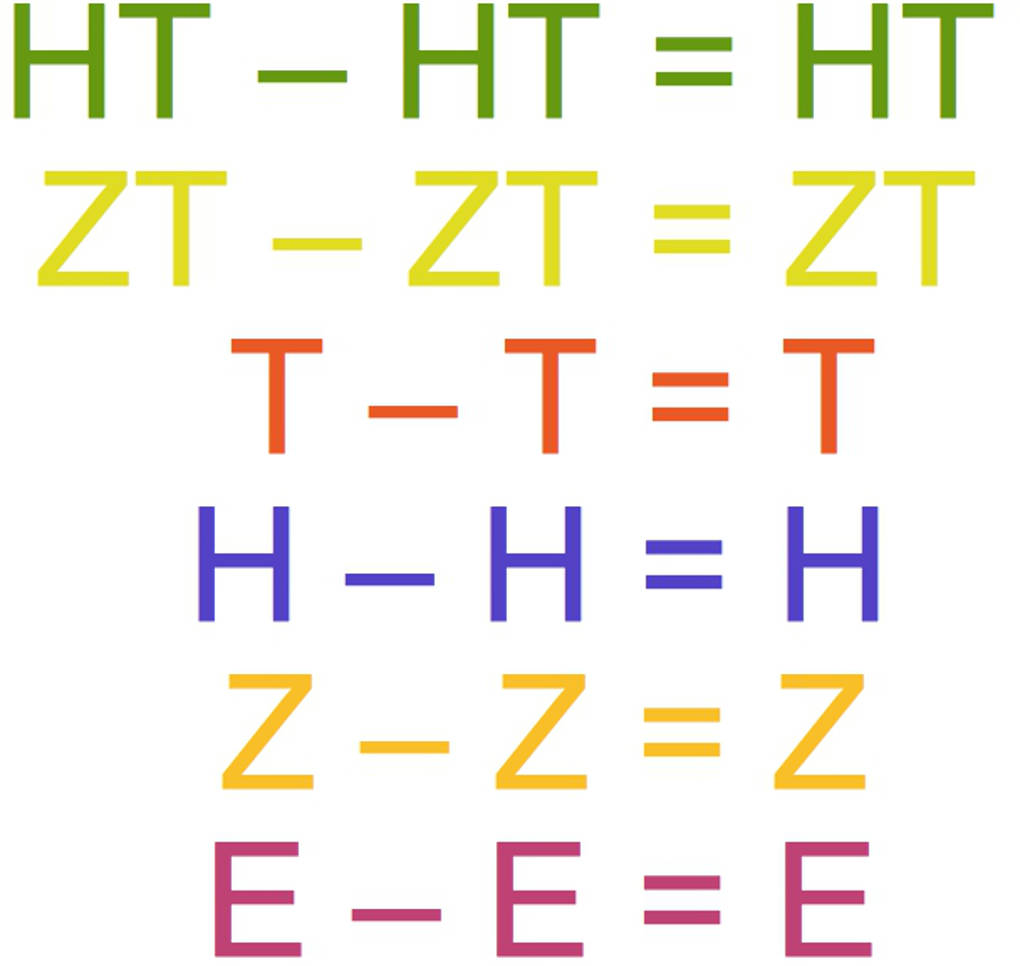
Wenn die jeweiligen Stellen des Minuenden immer größer sind oder gleich der entsprechenden Stelle des Subtrahenden, dann kannst du so rechnen:

- Du subtrahierst die jeweiligen Stellen voneinander, so wie du es hier sehen kannst.
- Zuletzt addierst du die Ergebnisse und erhältst die gesuchte Differenz.
Was kannst du tun, wenn die Stellen des Minuenden nicht alle größer oder gleich der des Subtrahenden sind?
Hier hilft ein Trick:
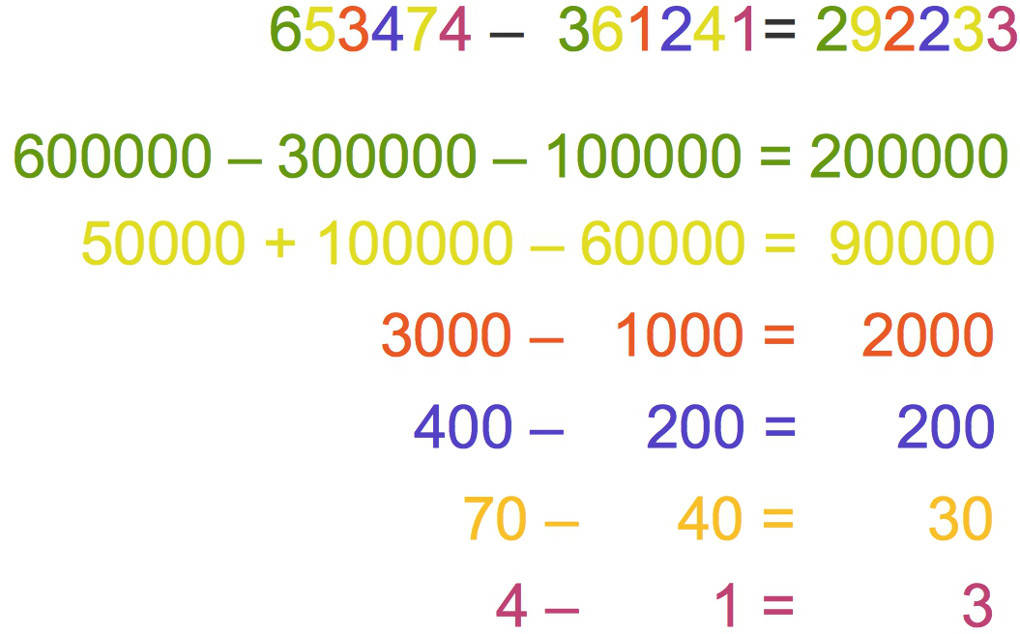
- Bei den Hunderttausendern kannst du so subtrahieren wie in dem obigen Beispiel. Aber Vorsicht!
- Bei den Zehntausendern kannst du nicht von 50000 die 60000 subtrahieren.
- Deshalb nimmst du von den Hunderttausendern 100000 weg. Du subtrahierst diese. Nun tust du sie zu den Zehntausendern dazu. Also addierst du sie. So erhältst du 50000 + 100000 - 60000 = 150000 - 60000 = 90000.
- Danach geht es wie in dem oberen Beispiel weiter.
Dieser Trick wird auch als Übertrag bezeichnet. Dieser wird beim schriftlichen Subtrahieren verwendet.
Schriftliches Subtrahieren
Beim schriftlichen Subtrahieren mit Übertrag werden Minuend und Subtrahend in einer Stellenwerttafel untereinander geschrieben. Vor den Subtrahenden schreibst du ein Minus-Zeichen und darunter machst du einen Strich. Im Gegensatz zum halbschriftlichen Subtrahieren beginnst du hier mit den Einern, also rechts. Du bildest Stelle für Stelle die Differenz und trägst das so erhaltene Ergebnis in dem entsprechenden Feld in der gleichen Spalte ein. Das Ergebnis der Subtraktionsaufgabe steht dann in der letzten Zeile.
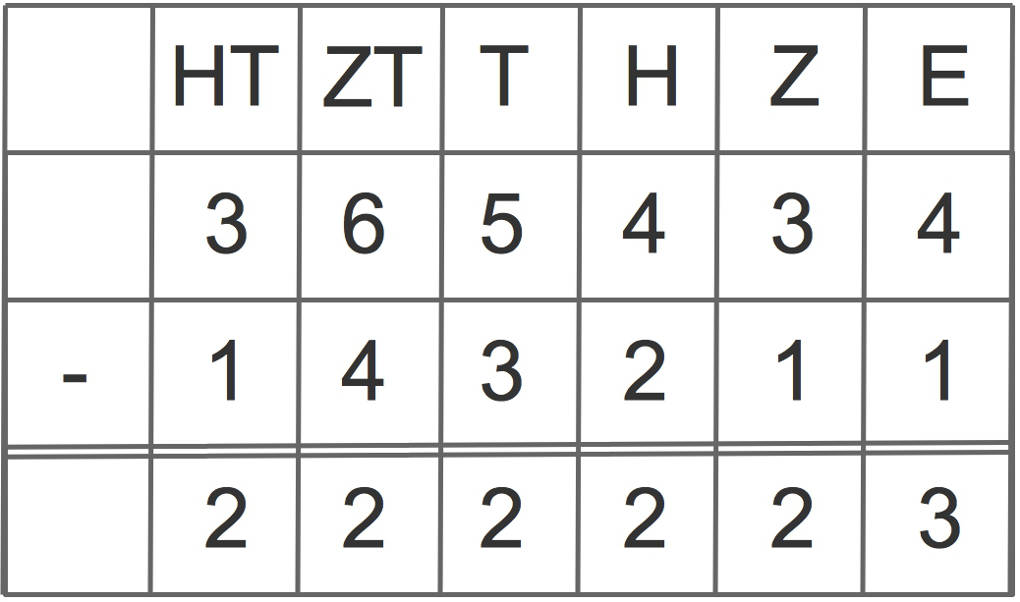
Hier kannst du für jede Stelle die Subtraktion durchführen. Nur was machst du, wenn dies nicht möglich ist?
Es soll die Differenz der beiden Zahlen 365434 sowie 183251 berechnet werden. Du gehst dabei ebenso vor wie bei dem obigen Beispiel.
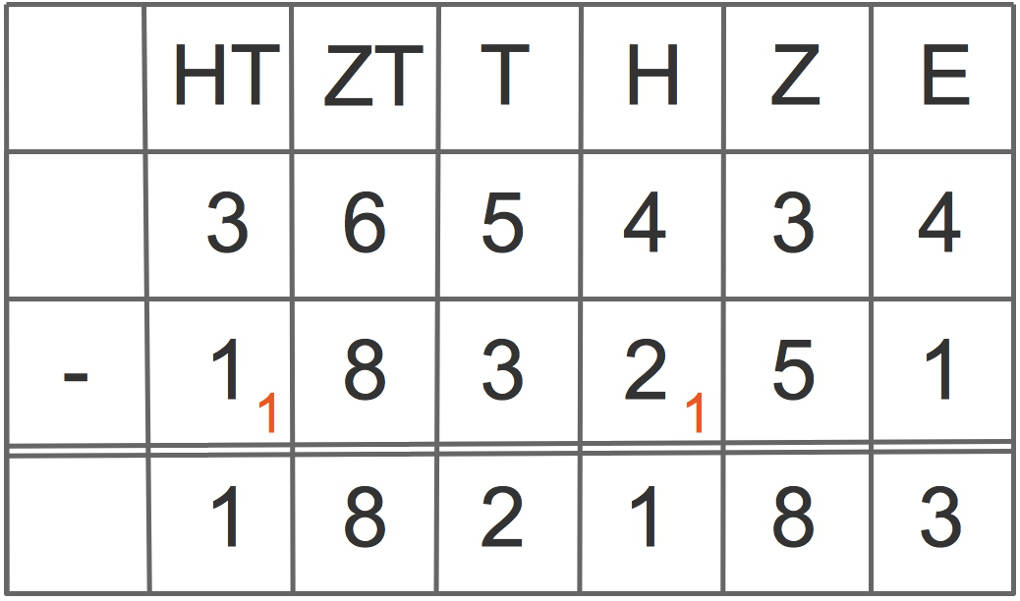
- Einer: 4 - 1 = 3. Dies ist der Eintrag in der Einer-Spalte.
- Zehner: 3 - 5, das geht nicht. Deshalb führst du einen Übertrag durch. Dieser ist an der roten 1 in der zweiten Zeile bei den Hundertern zu erkennen. Nun kannst du 13 - 5 = 8 rechnen. Dies ist der Eintrag in der Zehner-Spalte.
- Hunderter: Denke an den Übertrag! Du subtrahierst nicht 4 - 2, sondern addierst zunächst 2 + 1 = 3 und subtrahierst dann: 4 - 3 = 1. Dies ist der Eintrag in der Hunderter-Spalte.
- Tausender: 5 - 3 = 2. Dies ist der Eintrag in der Tausender-Spalte.
- Zehntausender: Hier machst du wieder einen Übertrag. 16 - 8 = 8. Dies ist der Eintrag in der Zehntausender-Spalte.
- Hunderttausender: Denke auch hier an den Übertrag. Addiere zunächst 1 + 1 = 2 und subtrahiere dann 3 - 2 = 1 Dies ist der Eintrag in der Hundertausender-Spalte.
- Das gesuchte Ergebnis ist 182183.
Alle Videos zum Thema
Videos zum Thema
Addition und Subtraktion: Halbschriftlich und schriftlich (19 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Addition und Subtraktion: Halbschriftlich und schriftlich (19 Arbeitsblätter)
-
 Halbschriftliche Addition
PDF anzeigen
Halbschriftliche Addition
PDF anzeigen -
 Halbschriftliches Addieren bis Zehntausend
PDF anzeigen
Halbschriftliches Addieren bis Zehntausend
PDF anzeigen -
 Wie geht schriftliches Addieren?
PDF anzeigen
Wie geht schriftliches Addieren?
PDF anzeigen -
 Schriftliches Addieren ohne Übertrag
PDF anzeigen
Schriftliches Addieren ohne Übertrag
PDF anzeigen -
 Schriftliches Addieren mit Übertrag
PDF anzeigen
Schriftliches Addieren mit Übertrag
PDF anzeigen -
 Wie geht schriftliches Subtrahieren? – Abziehverfahren
PDF anzeigen
Wie geht schriftliches Subtrahieren? – Abziehverfahren
PDF anzeigen -
 Wie geht schriftliches Subtrahieren? – Ergänzungsverfahren
PDF anzeigen
Wie geht schriftliches Subtrahieren? – Ergänzungsverfahren
PDF anzeigen -
 Schriftliches Subtrahieren mit Übertrag – Abziehverfahren
PDF anzeigen
Schriftliches Subtrahieren mit Übertrag – Abziehverfahren
PDF anzeigen -
 Schriftliches Subtrahieren mit Übertrag – Ergänzungsverfahren
PDF anzeigen
Schriftliches Subtrahieren mit Übertrag – Ergänzungsverfahren
PDF anzeigen -
 Grundrechenarten bis 1 Million – Sachaufgaben zur Addition
PDF anzeigen
Grundrechenarten bis 1 Million – Sachaufgaben zur Addition
PDF anzeigen -
 Schriftliches Addieren mit mehreren Zahlen
PDF anzeigen
Schriftliches Addieren mit mehreren Zahlen
PDF anzeigen -
 Schriftliches Addieren mit mehreren Zahlen – Übung
PDF anzeigen
Schriftliches Addieren mit mehreren Zahlen – Übung
PDF anzeigen -
 Über den Hunderter subtrahieren – von links nach rechts
PDF anzeigen
Über den Hunderter subtrahieren – von links nach rechts
PDF anzeigen -
 Grundrechenarten bis 1 Million – Sachaufgaben zur Subtraktion
PDF anzeigen
Grundrechenarten bis 1 Million – Sachaufgaben zur Subtraktion
PDF anzeigen -
 Halbschriftliches Subtrahieren bis 1 Million
PDF anzeigen
Halbschriftliches Subtrahieren bis 1 Million
PDF anzeigen -
 Schriftliches Subtrahieren mit zwei Überträgen (1)
PDF anzeigen
Schriftliches Subtrahieren mit zwei Überträgen (1)
PDF anzeigen -
 Schriftliches Subtrahieren mit zwei Überträgen (2)
PDF anzeigen
Schriftliches Subtrahieren mit zwei Überträgen (2)
PDF anzeigen -
 Schriftliches Subtrahieren mit mehreren Zahlen – Übung
PDF anzeigen
Schriftliches Subtrahieren mit mehreren Zahlen – Übung
PDF anzeigen -
 Einhaltung der schriftlichen Form
PDF anzeigen
Einhaltung der schriftlichen Form
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren


































