Potenzen mit negativen Exponenten
Weißt du bereits, was eine Potenz ist? Gut, dann schauen wir uns einmal an, was mit einer Potenz passiert, wenn der Exponent negativ ist.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was sind Potenzen?
Eine Potenz ist ein Term der Form $a^{n}$. Wenn $n$ eine natürliche Zahl ist, ist $a^n$ die abkürzende Schreibweise für ein Produkt, in welchem der Faktor $a$ gerade $n$-mal vorkommt: $a^{n}=\underbrace{a\cdot\ ...\ \cdot a}_{n-\text{mal}}$.
Dabei ist der Faktor $a$ die Basis der Potenz und die Häufigkeit $n$, wie oft der Faktor in dem Produkt vorkommt, der Exponent.
Hier siehst du eine Potenz sowie die zugehörigen Bezeichnungen im Überblick:
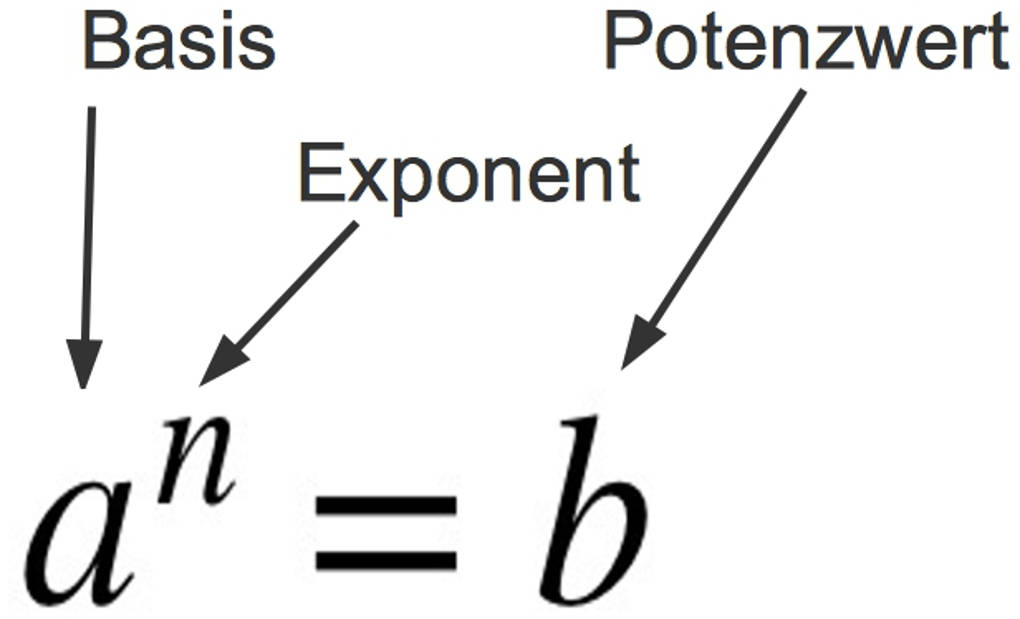
Ein Beispiel: $3^{4}=3\cdot 3\cdot 3\cdot 3=81$. Das Ergebnis einer Potenz, hier $81$, wird als Potenzwert bezeichnet.
Im Folgenden schauen wir uns nun an, welche Bedeutung ein negativer Exponent hat.
Potenzen mit negativen Exponenten
Schau dir einmal diese Zweierpotenz an:
- ...
- $2^{4}=2\cdot 2\cdot 2\cdot 2=16$
- $2^{3}=2\cdot 2\cdot 2=8$
- $2^{2}=2\cdot 2=4$
- $2^{1}=2$
Fällt dir etwas auf?
- Zum einen wird der Exponent immer kleiner: $...;~4;~3;~2;~1$.
- Zum anderen wird der Potenzwert immer halbiert: $...;~16;~8;~4;~2$.
Wie könnte es nun weitergehen?
- Wenn du den Exponenten nochmal um $1$ verringerst, erhältst du $0$. Den zugehörigen Potenzwert erhältst du, indem du $2$ halbierst, also $2:2=1$. Damit ist $2^{0}=1$. Verblüffend. Gib $2^0$ doch einmal zur Kontrolle in deinen Taschenrechner ein. Übrigens: $a^{0}=1$ für alle $a\neq 0$.
- Vermindere den Exponenten nun nochmal um $1$ zu $-1$. Dann musst du auch den Potenzwert halbieren zu $1:2=0,5$. Dann ist $2^{-1}=\frac12=0,5$.
Du kannst also die obige Liste weiterführen, allerdings nicht mehr mit der Schreibweise als Produkt:
- $2^{0}=1$
- $2^{-1}=\frac12=0,5$
- $2^{-2}=\frac1{2^{2}}=0,25$
- ...
Ganz allgemein gilt für Potenzen mit negativen Exponenten: $a^{-n}=\frac1{a^{n}}$. Dabei muss allerdings immer $a\neq 0$ gelten.
Im Zähler steht immer die $1$ und im Nenner die Potenz selbst. Allerdings vertauschst du beim Exponenten das Vorzeichen.
Beispiele: Im Folgenden geht es nicht um die Berechnung der Potenzwerte, sondern ausschließlich um die Anwendung der Definition von Potenzen mit negativen Exponenten.
- $3^{-4}=\frac1{3^{4}}$
- $5^{-2}=\frac1{5^{2}}$
- $7^{-3}=\frac1{7^{3}}$
- $\left(\frac12\right)^{-4}=\frac1{\left(\frac12\right)^{4}}$
Die Potenzgesetze
Die Potenzgesetze helfen dir beim Rechnen mit Potenzen. Im Folgenden schauen wir uns die ersten drei Potenzgesetze einmal für negative Exponenten an, denn da gelten die Gesetze auch:
Das 1. Potenzgesetz
Dieses Gesetz siehst du hier noch einmal in Worten formuliert: Potenzen mit gleicher Basis werden multipliziert, indem man die Basis beibehält und die Exponenten addiert.
Wir üben dies an einem Beispiel:
$5^{8}\cdot 5^{-5}=5^{8+({-5})}=5^{8-5}=5^3$
Das 2. Potenzgesetz
Dieses Gesetz besagt: Potenzen mit gleicher Basis werden dividiert, indem man die Basis beibehält und die Exponenten subtrahiert.
Die folgende Divisionsaufgabe lösen wir nun auf zwei Arten: $3^{5}:3^{8}$.
- Wende das 2. Potenzgesetz an. Du subtrahierst die Exponenten. Achte dabei unbedingt auf die Reihenfolge der Subtraktion: $3^{5}:3^{8}=3^{5-8}=3^{-3}$.
- Schreibe den Quotienten als Bruch, verwende die Erklärung einer Potenz als Produkt und kürze schließlich:
$3^{5}:3^{8}=\frac{3^{5}}{3^{8}}=\frac{\not 3\cdot \not 3\cdot \not 3\cdot \not 3\cdot \not 3~^{1}}{\not 3\cdot \not 3\cdot \not 3\cdot \not 3\cdot \not 3\cdot 3\cdot 3\cdot 3} =\frac1{3\cdot 3\cdot 3}=\frac1{3^{3}}$
- Fasse nun zusammen: $3^{-3}=\frac1{3^{3}}$.
Dieses Ergebnis wird dich jetzt sicherlich nicht mehr verwundern.
Das 3. Potenzgesetz
Weißt du noch, wie dieses Gesetz in Worten lautet? Potenzen werden potenziert, indem man die Basis beibehält und die Exponenten multipliziert.
Abschließend schauen wir uns noch Beispiele zu Potenzen von Potenzen an. Dabei soll jeweils mindestens ein Exponent negativ sein:
- $\left(3^{-2}\right)^{4}=3^{({-2})\cdot 4}=3^{-8}=\frac1{3^{8}}$
- $\left(5^{2}\right)^{-2}=5^{2\cdot ({-2})}=5^{-4}=\frac1{5^{4}}$
- $\left(4^{-1}\right)^{-2}=4^{({-1})\cdot ({-2})}=4^{2}$
Zusammenfassung und Ausblick
Die Exponenten können auch negativ und rational sein. Um zu verstehen, wie solche Potenzen aussehen, verwendest du zum einen dein Wissen über negative Exponenten, welches jetzt sicher sehr groß ist, und zum anderen das über rationale Exponenten.
Es gilt:
- $a^{0}=1$
- $a^{-n}=\frac1{a^{n}}$
Weiter gilt für $a\ge 0$ und rationale Exponenten:
- $a^{\frac mn}=\sqrt[n]{a^{m}}$
Somit gilt für $a\gt 0$ folgender Zusammenhang:
- $a^{-\frac mn}=\frac1{\sqrt[n]{a^{m}}}$
Das sieht sicher nicht sehr schön aus, aber keine Angst, schlimmer wird es nicht.
Alle Videos zum Thema
Videos zum Thema
Potenzen mit negativen Exponenten (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Potenzen mit negativen Exponenten (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter








 Negative Exponenten
Negative Exponenten
 Negative Zahlen oder Null als Exponent
Negative Zahlen oder Null als Exponent
 Exponentialschreibweise
Exponentialschreibweise









