Trigonometrische Funktionen
Trigonometrische Funktionen beschreiben die Verhältnisse von Winkeln und Längen im Einheitskreis. Sinus, Cosinus und Tangens sind die grundlegenden Funktionen. Entdecke, wie man sie am Einheitskreis abliest und berechnet. Interessiert? Weitere Details zur Definition und Anwendung findest du weiter unten im Text!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Lerntext zum Thema Trigonometrische Funktionen
Trigonometrische Funktionen – Definition
Die Trigonometrie ist ein Teilgebiet der Geometrie in der Mathematik. Sie befasst sich mit mathematischen Zusammenhängen zwischen Kreisbögen und rechtwinkligen Dreiecken.
Als trigonometrische Funktionen bezeichnet man Funktionen, die die Verhältnisse zwischen den Längen und Winkeln bzw. Bogenlängen im Einheitskreis und in rechtwinkligen Dreiecken bezeichnen.
Die elementaren trigonometrischen Funktionen sind die Sinusfunktion $\sin(\alpha)$, die Cosinusfunktion $\cos(\alpha)$ und die Tangensfunktion $\tan(\alpha)$.
Trigonometrische Funktionen werden auch Winkelfunktionen genannt, da sie einen Winkel
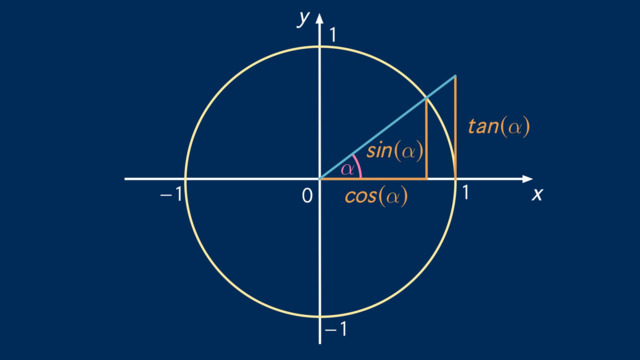
In der folgenden Abbildung siehst du einen Einheitskreis, also einen Kreis mit Radius $r = 1$. Hier ist eingezeichnet, wie sich die Längen, die

Du kannst dir hier vorstellen, wie sich $\sin(\alpha)$, $\cos(\alpha)$ und $\tan(\alpha)$ verändern, wenn der Winkel $\alpha$ andere Werte zwischen $0^\circ$ und $360^\circ$ annimmt. Die blaue Linie ($r = 1$) wandert mit zunehmendem Winkel $\alpha$ entgegen dem Uhrzeigersinn um den Mittelpunkt $M$. Dabei verändert sich ihre Länge nicht – die Längen der grünen, roten und orangen Linien ändern sich allerdings sehr wohl in Abhängigkeit von $\alpha$.
Wusstest du schon?
Die Sinus- und Kosinusfunktionen waren bereits im Griechenland der Antike bekannt! Der Mathematiker Hipparchos nutzte sie zum Beispiel, um die Positionen von Himmelskörpern zu berechnen. Also, das nächste Mal, wenn du den Sinuswinkel berechnest, denk daran: Du trittst in die Fußstapfen der antiken Sternenguckerinnen und Sternengucker!
Bogenlänge und Bogenmaß
Der Winkel $\alpha$ im Einheitskreis kann in Grad angegeben werden, aber auch mithilfe der Bogenlänge.
Der zu $\alpha$ gehörige Kreisbogen wird im ersten Quadranten von der $x$‑Achse und dem eingezeichneten
$\dfrac{b}{2\,\pi \cdot r} = \dfrac{\alpha}{360^\circ}$
Diese Gleichung können wir nach $b$ auflösen. Damit ist die Bogenlänge folgendermaßen definiert:
$b = \dfrac{2\,\pi \cdot r}{360^\circ} \cdot \alpha$
Da der Radius $r$ im Einheitskreis die Länge $1$ hat, lässt sich die Bogenlänge $b$ direkt aus dem Winkel $\alpha$ berechnen:
$b = \dfrac{2\,\pi \cdot 1}{360^\circ} \cdot \alpha = \dfrac{\pi}{180^\circ} \cdot \alpha$
Man sagt dann auch: $b$ ist der Winkel $\alpha$ im Bogenmaß.
Allgemein bezeichnet das Bogenmaß das Verhältnis der Bogenlänge zum Radius:
$\dfrac{b}{r} = \dfrac{\pi}{180^\circ} \cdot \alpha$
Bezieht man sich auf den Einheitskreis, entspricht das Bogenmaß direkt der Bogenlänge $b$ $\left(\frac{b}{1} = b \right)$ in der Einheit $\text{rad}$.
Diese Einheit leitet sich vom lateinischen Wort radiant ab. Die Einheitenbezeichnung $\text{rad}$ wird allerdings meist weggelassen, das heißt, Winkel im Bogenmaß (manchmal auch Winkelmaß genannt) werden einfach als Zahlen ohne Einheit geschrieben. Nur durch das $^\circ$‑Zeichen sind sie von Winkeln im Gradmaß zu unterscheiden.
Fehleralarm
Häufig wird der Winkel in Grad statt in Radiant gemessen, wenn trigonometrische Funktionen berechnet werden. Achtung: Das kann zu falschen Ergebnissen führen!
Darauf solltest du achten, wenn du mit dem Taschenrechner rechnest und verschiedene Winkel als Argument trigonometrischer Funktionen wie $\sin(\alpha)$, $\cos(\alpha)$ und $\tan(\alpha)$ eingibst. Mit den Befehlen $\text{DEG}$ (für degree) und $\text{RAD}$ (für radiant) kannst du zwischen Gradmaß und Bogenmaß wechseln.
Trigonometrische Funktionen – Formeln
Im Folgenden gehen wir auf die wichtigsten trigonometrischen Funktionen $\sin(\alpha)$, $\cos(\alpha)$ und $\tan(\alpha)$ ein und sehen uns an, wie diese in verschiedenen Formeln verwendet werden, um Verhältnisse zwischen Längen und Winkeln in rechtwinkligen Dreiecken zu bestimmen.
Trigonometrische Funktionen – Sinus
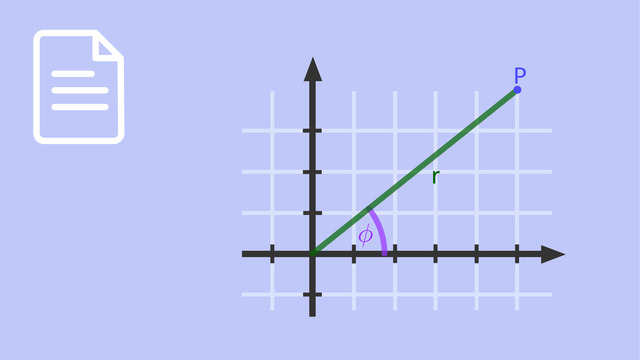
Jedes rechtwinklige Dreieck lässt sich in den ersten Quadranten eines Kreises setzen, so wie wir das in der Abbildung des Einheitskreises gesehen haben.
Die Seite, die den Mittelpunkt $M$ mit einem Punkt $P\left(x\,\vert\,y \right)$ auf dem Kreis
verbindet, hat dann die Länge des Radius $r$ – die im allgemeinen Fall jetzt nicht mehr gleich $1$ ist. Diese Seite ist die Hypotenuse des rechtwinkligen Dreiecks. Die beiden Katheten des Dreiecks haben die Längen $x$ und $y$, wenn man sich den Kreismittelpunkt $M$ als Ursprung eines kartesischen Koordinatensystems denkt.
Der rechte Winkel des Dreiecks wird von den beiden Katheten eingeschlossen und liegt der Hypotenuse gegenüber.
Der Winkel $\alpha$ wird von der Hypotenuse und der Kathete, die auf der
Als Sinus des Winkels $\alpha$ bezeichnet man nun das Verhältnis der Längen von Gegenkathete und Hypotenuse.
Merke:
$\text{Sinus von}~\alpha = \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} \Longleftrightarrow \sin(\alpha) = \dfrac{y}{r}$
Im Einheitskreis ist $r=1$ und deshalb gilt dort einfach $\sin(\alpha) = y$, wie in der Abbildung oben zu sehen (grüne Linie). Anhand des Einheitskreises kannst du dir auch verdeutlichen, welche verschiedenen Werte der Sinus für bestimmte Winkel $\alpha$ annimmt. Es gilt beispielsweise:
- $\sin(0^\circ) = 0$
- $\sin(30^\circ) = \frac{1}{2}$
- $\sin(45^\circ) = \frac{\sqrt{2}}{2}$
- $\sin(60^\circ) = \frac{\sqrt{3}}{2}$
- $\sin(90^\circ) = 1$
Im ersten Quadranten sind alle Werte des Sinus positiv. Für die beiden Grenzfälle $\sin(0^\circ) = 0$ und $\sin(90^\circ) = 1$ gibt es allerdings keine zugehörigen rechtwinkligen Dreiecke, da dann jeweils die Hypotenuse mit einer der beiden Katheten zusammenfällt.
Trigonometrische Funktionen – Cosinus
Analog zur Sinusfunktion definiert man die Cosinusfunktion. Sie bezieht sich auf die Kathete des rechtwinkligen Dreiecks, die im ersten Quadranten unseres gedachten Kreises auf der
Der Cosinus (auch: Kosinus) des Winkels $\alpha$ beschreibt folglich das Verhältnis der Längen von Ankathete und Hypotenuse.
Merke:
$\text{Cosinus von}~\alpha = \dfrac{\text{Ankathete}}{\text{Hypotenuse}} \Longleftrightarrow \cos(\alpha) = \dfrac{x}{r}$
Im Einheitskreis gilt einfach $\cos(\alpha) = x$ (rote Linie in der Abbildung oben).
Aus der Darstellung am Einheitskreis können wir wieder einige Werte ableiten, die der Cosinus für verschiedene Winkel $\alpha$ annimmt:
- $\cos(0^\circ) = 1$
- $\cos(30^\circ) = \frac{\sqrt{3}}{2}$
- $\cos(45^\circ) = \frac{\sqrt{2}}{2}$
- $\cos(60^\circ) = \frac{1}{2}$
- $\cos(90^\circ) = 0$
Im ersten Quadranten sind auch alle Werte des Cosinus positiv. Du kannst hier vielleicht schon erkennen, dass es einen gewissen Zusammenhang zwischen den Werten von $\sin(\alpha)$ und $\cos(\alpha)$ gibt. Das muss so sein, denn auch die Seitenlängen der zugehörigen rechtwinkligen Dreiecke sind abhängig voneinander.
Die Länge der Hypotenuse steht mit dem Radius fest (im Einheitskreis gleich $1$). Bei größeren Winkeln $\alpha$ wird (im ersten Quadranten) auch die Gegenkathete (im Einheitskreis $y = \sin\alpha$) größer, während die Länge der Ankathete (im Einheitskreis $x = \cos\alpha$) entsprechend abnimmt.
Trigonometrische Funktionen – Tangens
In unserer Abbildung des Einheitskreises ist die Seite, die dem Tangens entspricht (orange), nicht Teil des rechtwinkligen Dreiecks innerhalb des Kreises. Trotzdem hängt ihre Länge über die Strahlensätze mit den beiden Katheten des inneren Dreiecks zusammen.
Der Tangens des Winkels $\alpha$ drückt das Verhältnis der Längen von Gegenkathete und Ankathete aus.
Merke:
$\text{Tangens von}~\alpha = \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \Longleftrightarrow \tan(\alpha) = \dfrac{y}{x} = \dfrac{\sin(\alpha)}{\cos(\alpha)}$
Da der Tangens das Verhältnis zwischen Gegenkathete und Ankathete beschreibt, ist dessen Wert unabhängig vom Radius $r$. Somit gelten die Werte von $\tan(\alpha)$ des Einheitskreises auch für alle anderen Fälle $r \neq 1$.
Allerdings ist $\tan(\alpha)$ für $\alpha = 90^\circ$ bzw. für $\frac{b}{r} = \frac{\pi}{2}$ und alle ungeraden, ganzzahligen Vielfachen von $\frac{\pi}{2}$ nicht definiert. Denn dann würde das Seitenverhältnis $\frac{y}{x}$ gegen den Wert $\infty$ laufen bzw. der Nenner des Bruchs den Wert $0$ annehmen. Gleiches gilt natürlich hinsichtlich des Bruchs $\frac{\sin(\alpha)}{\cos(\alpha)}$. Diese Fälle sind also nicht erlaubt.
Sehen wir uns eine Werte an, die der Tangens für verschiedene Winkel $\alpha$ annimmt:
- $\tan(0^\circ) = \dfrac{\sin(0^\circ)}{\cos(0^\circ)} = \frac{0}{1} = 0$
- $\tan(30^\circ) = \dfrac{\sin(30^\circ)}{\cos(30^\circ)} = \frac{1\,\cdot\,2}{2\,\cdot\,\sqrt{3}} = \frac{1}{\sqrt{3}}$
- $\tan(45^\circ) = \dfrac{\sin(45^\circ)}{\cos(45^\circ)} = \frac{\sqrt{2}\,\cdot\,2}{2\,\cdot\,\sqrt{2}} = 1$
- $\tan(60^\circ) = \dfrac{\sin(60^\circ)}{\cos(60^\circ)} = \frac{\sqrt{3}\,\cdot\,2}{2\,\cdot\,1} = \sqrt{3}$
- $\tan(90^\circ) = \dfrac{\sin(90^\circ)}{\cos(90^\circ)} = \frac{1}{0} = \text{n. d. (nicht definiert)}$
Im ersten Quadranten sind alle Werte des Tangens positiv. Während die Werte von $\sin(\alpha)$ und $\cos(\alpha)$ im ersten Quadranten des Einheitskreises jeweils zwischen $0$ und $1$ liegen, nimmt $\tan(\alpha)$ allerdings alle positiven Werte zwischen $0$ und $\infty$ an.
So direkt, wie der Sinus und der Cosinus mit den Katheten des rechtwinkligen Dreiecks innerhalb des ersten Quadranten zusammenhängen, ist der Tangens leider nicht zu interpretieren. Trotzdem ist die Tangensfunktion ein wichtiges Hilfsmittel beim Rechnen mit Winkeln und Seitenverhältnissen, zum Beispiel auch bei der Berechnung der Steigung linearer Funktionsgraphen.
Trigonometrische Funktionen – Eigenschaften
Die wichtigste Eigenschaft aller trigonometrischen Funktionen ist, dass sie periodisch verlaufen, das heißt die Funktionswerte von $\sin(\alpha)$, $\cos(\alpha)$ und $\tan(\alpha)$ wiederholen sich nach einer bestimmten Periode wieder.
Das kannst du besonders gut am Einheitskreis nachvollziehen. Wenn der Winkel $\alpha$ Werte von $0^\circ$ bis $360^\circ$ annimmt, verändern sich mit ihm auch die Funktionswerte von $\sin(\alpha)$, $\cos(\alpha)$ und $\tan(\alpha)$. Aber nach $360^\circ$, also nach einem Umlauf um den Einheitskreis, wiederholt sich alles wieder.
Das heißt, bei Werten von $360^\circ \leq \alpha < 720^\circ$ werden entsprechend gleiche Funktionswerte $\sin(\alpha)$, $\cos(\alpha)$ und $\tan(\alpha)$ abgebildet wie zuvor bei $0^\circ \leq \alpha < 360^\circ$. Mit jedem weiteren Umlauf wächst der Winkel $\alpha$, also das Argument der trigonometrischen Funktionen, aber die Funktionswerte wiederholen sich periodisch mit der Periode $360^\circ$ (bzw. $2\,\pi$ im Bogenmaß). Das zeigt sich auch in den Funktionsgraphen der jeweiligen Funktionen.
Kennst du das?
Vielleicht hast du schon einmal einen Stein in einen ruhigen See geworfen und die Wellen beobachtet, die sich kreisförmig ausbreiten. Diese Wellenbewegung ähnelt den Sinus- und Kosinuskurven in der Mathematik, die auch wellenförmig verlaufen. Wenn du die Trigonometrie besser verstehst, kannst du nachvollziehen, wie Wellen in der Physik, Musik und sogar Licht funktionieren. Die Mathematik ist überall um uns herum, sogar in den kleinsten Wellen.
Trigonometrische Funktionen – Funktionsgraph
Sehen wir uns zuerst einmal beispielhaft den Funktionsgraphen der Sinusfunktion $\sin(x)$ an.
Auf der $x$‑Achse ist hier das Argument der Funktion, also der Winkel $\alpha$ aufgetragen – allerdings nicht in Grad, sondern im Bogenmaß als Vielfaches der Kreiszahl $\pi$. In dieser Darstellung entspricht $\frac{1}{2}\,\pi$ einem Winkeln von $90^\circ$, $\pi$ einem Winkel von $180^\circ$ und so weiter.
In $y$‑Richtung sind die Funktionswerte $\sin(x)$ aufgetragen, wobei $x$ eben dem Winkel $\alpha$ im Bogenmaß entspricht.
Die Periode $2\,\pi \left(= 360^\circ \right)$ haben wir hier von einem Hochpunkt zum nächsten eingetragen, wir hätten sie aber genauso gut von Tiefpunkt zu Tiefpunkt oder zwischen zwei anderen Punkten eintragen können, an denen sich sowohl der $y$‑Wert als auch die Krümmungsrichtung des Graphen aufgrund der Periodizität wiederholen.
Trigonometrische Funktionen – Argument
Für das Argument der trigonometrischen Funktionen wird üblicherweise die Variable $\alpha$ verwendet, wenn es sich dabei um einen Winkel im Gradmaß handelt. Wird stattdessen $\sin(x)$ oder manchmal auch $\sin(\varphi)$ geschrieben, wird das Argument $x$ (bzw. $\varphi$) in der Regel im Bogenmaß angegeben – so auch in unserer Abbildung.
Im Bogenmaß liegen die Hochpunkte und Tiefpunkte der Sinusfunktion bei ungeraden, ganzzahligen Vielfachen von $\frac{\pi}{2}$ und haben die Funktionswerte $1$ bzw. $-1$.
Bei geraden, ganzzahligen Vielfachen von $\frac{\pi}{2}$ hat die Sinusfunktion hingegen den
Trigonometrische Funktionen – Nullstellen
Wie bereits erwähnt, liegen die Nullstellen der Sinusfunktion bei geraden, ganzzahligen Vielfachen von $\frac{\pi}{2}$. Das ist gleichbedeutend mit allen ganzzahligen Vielfachen von $\pi$. Wir können also formulieren:
$\sin(x_k) = 0$ für alle Nullstellen $x_k = k \cdot \pi$ mit $k \in \mathbb{Z}$
Die Cosinusfunktion verläuft ganz ähnlich wie die Sinusfunktion, allerdings hat $\cos(x)$ genau dort Hoch- und Tiefpunkte, wo $\sin(x)$ Nullstellen hat und genau dort Nullstellen, wo die Hoch- und Tiefpunkte der Sinusfunktion liegen.
Kurz gesagt: Die Cosinusfunktion entspricht einer Verschiebung der Sinusfunktion um $\frac{\pi}{2}$. Es gilt:
$\cos(x) = \sin \left( x + \frac{\pi}{2} \right)$
Also liegen die Hochpunkte und Tiefpunkte der Cosinusfunktion bei ganzzahligen Vielfachen von $\pi$ und die Nullstellen bei ungeraden, ganzzahligen Vielfachen von $\frac{\pi}{2}$. Wir können also formulieren:
$\cos(x_k) = 0$ für alle Nullstellen $x_k = \frac{\pi}{2} + k \cdot \pi$ mit $k \in \mathbb{Z}$
Die Tangensfunktion hat Nullstellen bei den gleichen Werten wie die Sinusfunktion, denn es gilt ja:
$\tan(x) = \dfrac{\sin(x)}{\cos(x)}$
Der Bruch $\frac{\sin(x)}{\cos(x)}$ nimmt immer dann den Wert $0$ an, wenn der Zähler, also $\sin(x)$, gleich $0$ ist. Es gilt also:
$\tan(x_k) = 0$ für alle Nullstellen $x_k = k \cdot \pi$ mit $k \in \mathbb{Z}$
Trigonometrische Funktionen – Wertebereich
Die Sinusfunktion und die Cosinusfunktion haben keine Definitionslücken, sind also für alle
Sinus- und Cosinusfunktion:
Definitionsbereich $D\,:\,x \in \mathbb{R}$
Wertebereich $W\,:\,y \in [-1\,;\,1 ]$
Bei der Tangensfunktion ist das etwas anders. Die Funktion $\tan(x) = \frac{\sin(x)}{\cos(x)}$ ist an allen Nullstellen von $\cos(x)$ nicht definiert, denn in diesen Fällen würde der Nenner des Bruchs den Wert $0$ annehmen. Außerdem kann $\tan(x)$ jeden reellen Wert $y$ annehmen. Die Tangensfunktion hat keine Hoch- oder Tiefpunkte, also keine relativen Extrema. Es gilt:
Tangensfunktion:
Definitionsbereich $D\,:\,x \in \mathbb{R} \setminus \{ \frac{\pi}{2} + k \cdot \pi \}$ mit $k \in \mathbb{Z}$
Wertebereich $W\,:\,y \in \mathbb{R}$
Trigonometrische Funktionen – Amplitude, Periode und Symmetrie
Wir haben bereits erwähnt, das $\sin(x)$ und $\cos(x)$ an ihren Hoch- und Tiefpunkten jeweils die Funktionswerte $1$ und $-1$ annehmen. Die Funktionswerte der beiden Winkelfunktionen pendeln also zwischen diesen beiden Extremwerten periodisch hin und her, wie ein schwingendes Pendel.
In der Tat werden die Sinus- und die Cosinusfunktion genutzt, um Schwingungen, also periodische Vorgänge wie die Schwingung eines Pendels, mathematisch zu beschreiben. Die maximale Auslenkung eines Pendels nach links und rechts entspricht dann beispielsweise genau den Hoch- und Tiefpunkten der Sinusfunktion, die periodisch immer und immer wieder erreicht werden.
Die maximale Auslenkung einer Schwingung wird auch Amplitude genannt. In diesem Sinne haben sowohl die Sinus- als auch die Cosinusfunktion eine Amplitude mit dem Betrag $a = 1$.
Die Tangensfunktion hat hingegen keine Amplitude, weil sie keine Hoch- und Tiefpunkte hat.
Bezogen auf rechtwinklige Dreiecke können wir uns die Amplitude so vorstellen: Wir können verschiedene Dreiecke mit einem rechten Winkel und einem beliebigen Winkel $\alpha < 90^\circ$ bilden. Je nach Größe des Winkels $\alpha$ kann eine der beiden Katheten theoretisch höchstens so lang werden wie die Hypotenuse. Auf dem Einheitskreis entspricht das der Länge $r = 1$.
Die Amplitude von $\sin(x)$ und $\cos(x)$ entspricht also jeweils der maximal möglichen Kathetenlänge: dem Radius $r = 1$.
So wie ein Pendel im Idealfall (also bei Vernachlässigung der Reibung) unendlich oft zwischen zwei Extrempunkten hin und her schwingt, so kann der Winkel $\alpha$ als Argument der Winkelfunktionen unendlich oft den Einheitskreis abfahren und dabei immer wieder die gleichen Funktionswerte $\sin(\alpha)$, $\cos(\alpha)$ und $\tan(\alpha)$ – bzw. im Bogenmaß $\sin(x)$, $\cos(x)$ und $\tan(x)$ – produzieren.
Obwohl $\sin(x)$ und $\cos(x)$ ihre Hoch- und Tiefpunkte an jeweils unterschiedlichen Stellen erreichen, ist ihre Periode gleich – sie hat bei beiden Funktionen den Wert $2\,\pi$. Das heißt, nach $360^\circ$ – oder eben $2\,\pi$ – wiederholen sich die Funktionswerte jeweils wieder. Hochpunkt folgt auf Hochpunkt im Abstand von $2\,\pi$ auf der $x$‑Achse und für die Tiefpunkte gilt das Gleiche. Mathematisch können wir diese Periodizität so ausdrücken:
$\sin(x) = \sin(x + p)$ mit $p = 2\,\pi$
$\cos(x) = \cos(x + p)$ mit $p = 2\,\pi$
Für die Tangensfunktion gilt hingegen:
$\tan(x) = \tan(x + p)$ mit $p = \pi$
Die Funktionswerte von $\tan(x)$ wiederholen sich also mit der Periode $p = \pi$ statt $2\,\pi$.
Das können wir anhand des Funktionsgraphen der Tangensfunktion nachvollziehen, die in der folgenden Abbildung dargestellt ist.

Hier siehst du außerdem, dass die Tangensfunktion punktsymmetrisch zum Koordinatenursprung ist. Das heißt, es gilt:
$\tan(x) = -\tan(-x)$
Auch die Sinusfunktion ist punktsymmetrisch zum Ursprung, wie du in der Abbildung weiter oben nachvollziehen kannst. Es gilt also auch:
$\sin(x) = -\sin(-x)$
Die Cosinusfunktion ist hingegen achsensymmetrisch zur $x$‑Achse. Es gilt:
$\cos(x) = \cos(-x)$
In der folgenden Abbildung ist der Funktionsgraph von $\cos(x)$ dargestellt, zusammen mit allen wichtigen Betrachtungen, die wir zu dieser Funktion aufgestellt haben.

Für die Sinus- und die Tangensfunktion haben wir all diese Betrachtungen ebenfalls herausgearbeitet. Damit kannst du dir eine eigene Übersicht mit allen drei Winkelfunktionen erstellen und die für dich wichtigen Punkte darauf notieren.
Trigonometrische Funktionen – Parameter
Wir haben die grundlegenden trigonometrischen Funktionen bisher in ihren einfachsten Formen $\sin(x)$, $\cos(x)$ und $\tan(x)$ betrachtet. Diese können allerdings auch mittels verschiedener Parameter modifiziert werden. Eine Sinusfunktion kann beispielsweise auch in dieser Form vorliegen:
$f(x) = a \cdot \sin(b \cdot x + c) + d$
Hier haben wir die Parameter $a$, $b$, $c$ und $d$. Sehen wir uns an, was diese bedeuten.
Den Parameter $a$ haben wir im Prinzip schon kennengelernt. Das ist die Amplitude der Sinusfunktion. Im einfachen Fall $\sin(x)$ hatten wir $a = 1$, aber im Fall $a \cdot \sin(x)$ kann $a$ auch jede andere reelle Zahl sein. Die Amplitude entspricht dem größtmöglichen $y$‑Wert, also der $y$‑Koordinate der Hochpunkte der Sinusfunktion.
Ist $a > 1$, handelt es sich demnach um eine Streckung der Sinusfunktion in $y$‑Richtung.
Mit $0 < a < 1$ erreichen wir hingegen eine Stauchung.
Mit einem negativen $a$ wird der Funktionsgraph zusätzlich an der $x$‑Achse gespiegelt, das heißt, Hoch- und Tiefpunkte tauschen die Plätze.Durch den Parameter $b$ verändert sich die Periode der Sinusfunktion. Das heißt, die Abstände auf der $x$‑Achse, in denen sich Nullstellen und Extremstellen abwechseln und wiederholen, werden kleiner oder größer.
Ist $b > 1$, werden die Abstände und damit auch die Periode kleiner, es handelt sich um eine Stauchung in $x$‑Richtung.
Mit $0 < b < 1$ wird hingegen eine Streckung erreicht, die Periode wird größer.
Mit einem negativen $b$ wird der Funktionsgraph zusätzlich an der $y$‑Achse gespiegelt, was wiederum zu einer Vertauschung der Hoch- und Tiefpunkte führt.Der Parameter $c$ führt zu einer Verschiebung der Sinusfunktion entlang der $x$‑Achse. Dafür haben wir schon ein Beispiel gesehen, nämlich die Verschiebung um den Wert $c = \frac{\pi}{2}$, mit der die Sinusfunktion genau deckungsgleich zur Cosinusfunktion wird:
$\cos(x) = \sin \left( x + \frac{\pi}{2} \right)$
Man nennt $c$ auch Phase bzw. spricht von einer Phasenverschiebung.
Eine Phasenverschiebung, die genau dem Wert $p$ der Periode entspricht, hat keinen Effekt, denn es gilt ja: $\sin(x + p) = \sin(x)$
Allerdings ändert sich dieser Wert $p$, wenn es einen Parameter $b \neq 1$ gibt. Für die Sinus- und Cosinusfunktion kann die Periode $p$ mit folgender Formel ermittelt werden: $p = \frac{2\,\pi}{b}$Der Parameter $d$ führt zu einer Verschiebung des Funktionsgraphen entlang der $y$‑Achse. Das ist bei den Winkelfunktionen nicht anders als bei allen anderen Arten von Funktionen.
Wusstest du schon?
Sinus und Kosinus sind auch in der Musik zu finden! Elektronische Musikinstrumente wie Synthesizer nutzen diese Funktionen, um elektrische Signale in Töne umzuwandeln. Jede gespielte Note ist im Grunde eine Schwingung, die durch trigonometrische Funktionen beschrieben und modelliert werden kann. Rock on, Mathematik!
Trigonometrische Funktionen – Rechenregeln
Bei der Betrachtung der trigonometrischen Funktionen bei rechtwinkligen Dreiecken haben wir uns auf den ersten Quadranten des Einheitskreises mit einem Winkel $0^\circ \leq \alpha \leq 90^\circ$ beschränkt. Bei der Untersuchung der Eigenschaften der trigonometrischen Funktionen haben wir unsere Betrachtungen allerdings auf $x \in \mathbb{R}$ im Bogenmaß erweitert.
Beim Rechnen mit dem Taschenrechner macht das keinen Unterschied, solange du berücksichtigst, wann es sich um einen Winkel in Grad und wann um eine Angabe im Bogenmaß handelt.
Wenn Winkelfunktionen verwendet werden, um periodische Vorgänge wie Schwingungen und Wellen zu beschreiben, ist es immer hilfreich, den Vorgang im Kopf einmal durchzuspielen. Beginnt die Schwingung mit dem Durchlaufen des Nullpunkts, ist der Sinus die passende Funktion, denn $\sin(0) = 0$. Beginnt sie hingegen mit der maximalen Auslenkung, wird sie durch den Cosinus besser beschrieben, denn $\cos(0) = 1$.
Versuche dir immer vorzustellen, wo auf dem Einheitskreis sich ein bestimmter Vorgang gerade abspielt. Und präge dir am besten die wichtigsten Werte der Winkelfunktionen gut ein:
| $\alpha$ | $x$ | $\sin(x)$ | $\cos(x)$ | $\tan(x)$ |
|---|---|---|---|---|
| $360^\circ$ | $2\,\pi$ | $0$ | $1$ | $0$ |
| $270^\circ$ | $\frac{3}{2}\,\pi$ | $-1$ | $0$ | $\text{n. d.}$ |
| $180^\circ$ | $\pi$ | $0$ | $-1$ | $0$ |
| $120^\circ$ | $\frac{2}{3}\,\pi$ | $\frac{\sqrt{3}}{2}$ | $-\frac{1}{2}$ | $-\sqrt{3}$ |
| $90^\circ$ | $\frac{1}{2}\,\pi$ | $1$ | $0$ | $\text{n. d.}$ |
| $60^\circ$ | $\frac{1}{3}\,\pi$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | $\sqrt{3}$ |
| $45^\circ$ | $\frac{1}{4}\,\pi$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $1$ |
| $30^\circ$ | $\frac{1}{6}\,\pi$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{3}}$ |
| $0^\circ$ | 0 | $0$ | $1$ | $0$ |
| $-30^\circ$ | $-\frac{1}{6}\,\pi$ | $-\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $-\frac{1}{\sqrt{3}}$ |
| $-45^\circ$ | $-\frac{1}{4}\,\pi$ | $-\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $-1$ |
| $-60^\circ$ | $-\frac{1}{3}\,\pi$ | $-\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | $-\sqrt{3}$ |
| $-90^\circ$ | $-\frac{1}{2}\,\pi$ | $-1$ | $0$ | $\text{n. d.}$ |
| $-120^\circ$ | $-\frac{2}{3}\,\pi$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{1}{2}$ | $\sqrt{3}$ |
| $-180^\circ$ | $-\pi$ | $0$ | $-1$ | $0$ |
| $-270^\circ$ | $-\frac{3}{2}\,\pi$ | $1$ | $0$ | $\text{n. d.}$ |
| $-360^\circ$ | $-2\,\pi$ | $0$ | $1$ | $0$ |
($\text{n. d.}$ steht für $\text{nicht definiert}$)
Kannst du die Systematiken erkennen, die sich aufgrund der Periodizität der Winkelfunktionen ergeben? Die Vorzeichen der Funktionswerte ergeben sich direkt aus den $x$‑ und $y$‑Achsen des Einheitskreises. Je nach Winkel landet man dort in einem der vier Quadranten.
- Im ersten Quadranten $\left( 0^\circ \leq \alpha < 90^\circ \right)$ sind $\sin(x)$, $\cos(x)$ und $\tan(x) \geq 0$
- Im zweiten Quadranten $\left( 90^\circ \leq \alpha < 180^\circ \right)$ ist $\sin(x) > 0$, aber $\cos(x)$ und $\tan(x) \leq 0$
- Im dritten Quadranten $\left( 180^\circ \leq \alpha < 270^\circ \right)$ sind $\sin(x)$, $\cos(x)$ und $\tan(x) \leq 0$
- Im vierten Quadranten $\left( 270^\circ \leq \alpha < 360^\circ \right)$ sind $\sin(x)$ und $\tan(x) < 0$, aber $\cos(x) \geq 0$
- Negative Winkel entsprechen einer Drehung im Uhrzeigersinn. So landet man beispielsweise für $\left( -90^\circ \leq \alpha < 0^\circ \right)$ im vierten Quadranten und erhält entsprechende Funktionswerte. Deshalb gilt beispielsweise: $\sin(-90^\circ) = \sin(270^\circ) = -1$
Den Verlauf der drei elementaren trigonometrischen Funktionen über $0 \leq x \leq 2\,\pi$, also einen Umlauf des Einheitskreises, haben wir in der folgenden Abbildung noch einmal skizziert.

Hier kannst du alle Funktionswerte und auch die Beziehung $\cos(x) = \sin \left( x + \frac{\pi}{2} \right)$, also die Verschiebung der Cosinusfunktion gegenüber der Sinusfunktion auf der $x$‑Achse, noch einmal nachvollziehen.
Auch die Polstellen der Tangensfunktion, also deren Definitionslücken, sind hier noch einmal deutlich zu sehen.
Trigonometrische Funktionen – Aufgaben
Ausblick – das lernst du nach Trigonometrische Funktionen
Begib dich auf die spannende Reise der Analytischen Geometrie! Mit Vektoren und der Addition und Subtraktion von Vektoren kannst du dein Wissen erweitern. Entdecke, wie verschiedene mathematische Konzepte miteinander verknüpft sind und freue dich auf weitere mathematische Entdeckungen!
Zusammenfassung der trigonometrischen Funktionen
- Mit trigonometrischen Funktionen werden die Verhältnisse von Längen und Winkeln in rechtwinkligen Dreiecken in Bezug auf den Einheitskreis beschrieben.
- Die grundlegenden trigonometrischen Funktionen sind die Sinusfunktion $\sin(\alpha)$, die Cosinusfunktion $\cos(\alpha)$ und die Tangensfunktion $\tan(\alpha)$.
- Sinus, Cosinus und Tangens können auch als $\sin(x)$, $\cos(x)$ und $\tan(x)$ in Abhängigkeit von $x$ im Bogenmaß geschrieben werden.
- Die Funktionswerte der Sinus- und Cosinusfunktion liegen stets zwischen $-1$ und $1$ und wiederholen sich periodisch mit der Periode $2\,\pi$ bzw. $360^\circ$. Auch die Tangensfunktion ist periodisch, allerdings mit der Periode $\pi$.
- Für rechtwinklige Dreiecke gelten folgende Formeln in Bezug auf den Winkel $\alpha$, der von der Hypotenuse und der Ankathete des Dreiecks eingeschlossen wird:
| trigonometrische Funktion | Seitenverhältnis |
|---|---|
| $\sin(\alpha)$ | $= \dfrac{\text{Gegenkathete}~y}{\text{Hypotenuse}~r}$ |
| $\cos(\alpha)$ | $= \dfrac{\text{Ankathete}~x}{\text{Hypotenuse}~r}$ |
| $\tan(\alpha)$ | $= \dfrac{\text{Gegenkathete}~y}{\text{Ankathete}~x}= \dfrac{\sin(\alpha)}{\cos(\alpha)}$ |
Häufig gestellte Fragen zum Thema Trigonometrische Funktionen
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.276
Lernvideos
38.589
Übungen
33.616
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?