Grenzwerte x gegen xₒ
Testeinsetzung, h-Methode, x0-Methode, linksseitiger Grenzwert, rechtsseitiger Grenzwert, Sprungstelle, hebbare Lücken, Definitionsbereich, Polstelle
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Grenzwertberechnung
Die Grenzwertberechnung $\lim\limits_{x\to x_{0}} f(x)$ findet zum einen Anwendung bei der Untersuchung des Verhaltens von Funktionsgraphen von Funktionen mit Definitionslücken. Zum anderen wird diese Grenzwertberechnung verwendet zur Definition der Ableitung einer Funktion an einer Stelle $x_{0}$:
$f'(x_{0})=\lim\limits_{x\to x_{0}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}$
Es gibt verschiedene Möglichkeiten, einen solchen Grenzwert zu berechnen. Diese siehst du hier im Überblick:
- Testeinsetzen
- Termumformung
- h-Methode
Jedes dieser Verfahren schauen wir uns nun an Beispielen an.
Übrigens: Wenn die stetige Funktion $f$ für $x=x_{0}$ definiert ist, gilt $\lim\limits_{x\to x_{0}} f(x)=f\left(x_{0}\right)$.
Testeinsetzen
Gegeben ist die gebrochenrationale Funktion $f$ mit $f(x)=\frac{x^{2}-1}{x-1}$ mit dem Definitionsbereich $\mathbb{D}=\mathbb{R}\setminus\{1\}$. Du sollst überprüfen, wie sich der Funktionsgraph an der Definitionslücke $x_{0}=1$ verhält.
Hierfür untersuchst du den Grenzwert $\lim\limits_{x\to 1}\frac{x^{2}-1}{x-1}$.
Bei der Methode des Testeinsetzens wählst du eine Folge, die gegen $1$ geht, zum Beispiel $0,9$; $0,99$; $0,999$; ... Wenn du die Anzahl der $9$-en hinter dem Komma immer weiter erhöhst, geht diese Folge gegen $1$. Du setzt nun diese verschiedenen $x$-Werte in die Funktionsgleichung ein:
$\begin{array}{c|c|c|c|c|c} x&0,9&0,99&0,999&0,9999&\to 1\\ \hline f(x)&1,9&1,99&1,999&1,9999&\to 2 \end{array}$
Da die Folge sich von links an $1$ annähert, spricht man hier von dem linksseitigen Grenzwert. Ebenso kannst du den rechtsseitigen Grenzwert berechnen. Dieser ist bei diesem Beispiel übrigens ebenfalls $2$.
Wenn links- und rechtsseitiger Grenzwert endlich sind und übereinstimmen, wird die Definitionslücke, in diesem Beispiel $x_{0}=1$, als behebbar bezeichnet.
Behebbare Definitionslücken werden im Funktionsgraphen ausgeschlossen. Dies kannst du zum Beispiel durch einen Kreis andeuten. Hier siehst du den Funktionsgraphen zu der oben angegebenen Funktion.
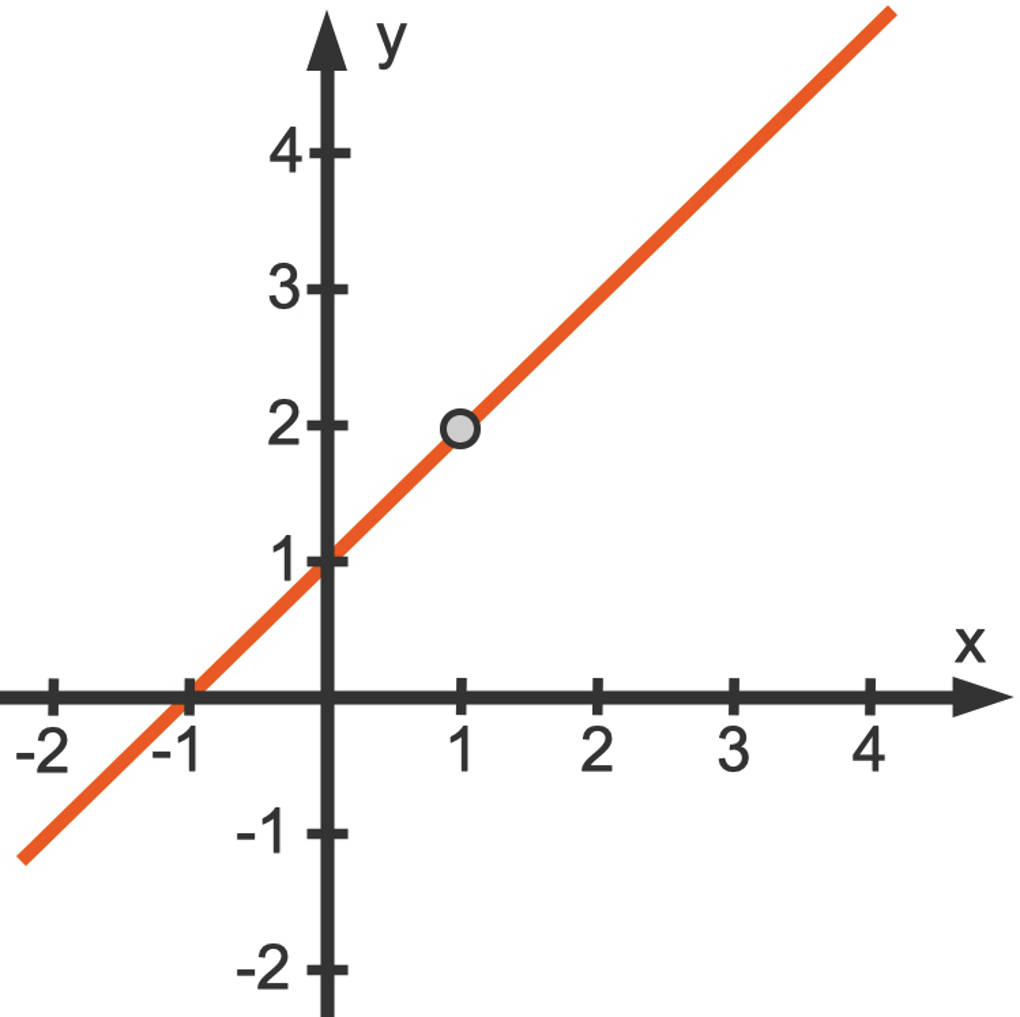
Es gibt auch Beispiele, bei welchen links- und rechtsseitiger Grenzwert ebenfalls endlich sind, allerdings nicht übereinstimmen. In diesem Fall liegt eine Sprungstelle des Funktionsgraphen vor.
Das Verfahren des Testeinsetzens kannst du übrigens auch bei Grenzwertbetrachtungen „$x\to\pm \infty$“ verwenden.
Termumformung
Bei der Termumformung kannst du entweder eine binomische Formel verwenden oder die Polynomdivision.
Dieses Verfahren siehst du nun am Beispiel der Ableitung der Funktion $f$ mit $f(x)=x^{2}-2x$.
Es ist
- $f'(x_{0})=\lim\limits_{x\to x_{0}}\frac{x^{2}-2x-\left(x_{0}^2-2x_{0}\right) }{x-x_{0}}$
- Sortiere die Terme rechts des Gleichheitszeichens zu $\lim\limits_{x\to x_0}\frac{x^2-x_0^2-\left(2x-2x_0\right)}{x-x_0}$.
- Wende eine Grenzwertregel an sowie die 3. binomische Formel: $\lim\limits_{x\to x_0}\frac{x^2-x_0^2}{x-x_0}-\lim\limits_{x\to x_0}\frac{2x-2x_0}{x-x_0}=\lim\limits_{x\to x_0}\frac{\left(x+x_0\right)\left(x-x_0\right)}{x-x_0}-\lim\limits_{x\to x_0}\frac{2x-2x_0}{x-x_0}$
- Nun kannst du jeweils $x-x_0$ kürzen zu $\lim\limits_{x\to x_0}\left(x+x_0\right)-\lim\limits_{x\to x_0}2=2x_0-2$.
Insgesamt erhältst du somit $f'(x_0)=2x_0-2$.
Wenn du keine binomische Formel anwenden kannst, um den Bruchterm zu kürzen, kannst du auch die Polynomdivision verwenden.
Du kannst in der oben gegebenen gebrochenrationalen Funktion $f$ mit $f(x)=\frac{x^{2}-1}{x-1}$ auch die 3. binomische Formel anwenden. Dann erhältst du durch Kürzen $f(x)=x+1$. Mit dieser Funktionsgleichung erhältst du ebenfalls den oben berechneten Grenzwert $\lim\limits_{x\to 1}f(x)=1+1=2$.
Die h-Methode
Anstatt den Grenzwert „$\lim\limits_{x\to x_0}$“ zu betrachten, kannst du auch „$x=x_0+h$“ betrachten und damit den Grenzwert „$\lim\limits_{h\to 0}$“. Da in diesem Verfahren $h$ betrachtet wird, spricht man von der h-Methode.
Dieses Verfahren wenden wir auf das obige Beispiel an:
$f'(x_{0})=\lim\limits_{h\to 0}\frac{\left(x_0+h\right)^{2}-2(x_0+h)-\left(x_{0}^2-2x_{0}\right) }{h}$
Du siehst, diese Rechnung sieht so ähnlich aus wie die obige. Dabei ist $x$ durch $x_0+h$ ersetzt worden.
Und los geht's:
- Wende die 1. binomische Formel an: $\lim\limits_{h\to 0}\frac{x_0^2+2\cdot x_0\cdot h+h^2-2x_0-2h-x_{0}^2+2x_{0}}{h}$.
- Nun kannst du die Terme im Zähler zusammenfassen zu $\lim\limits_{h\to 0}\frac{2\cdot x_0\cdot h+h^2-2h}{h}$.
- Klammere im Zähler $h$ aus und kürze dann mit $h$: $\lim\limits_{h\to 0}\frac{h\left(2x_0+h-2\right)}{h}=\lim\limits_{h\to 0}\left(2x_0+h-2\right)$.
- Zuletzt kannst du die einzelnen Summanden betrachten und deren Grenzwerte berechnen. So erhältst du $f'(x_0)=2x_0-2$.
So, nun ist es an dir zu entscheiden, welches der Verfahren dir am besten gefällt.
Ein Hinweis noch: Das Verfahren des Testeinsetzens ist mathematisch nicht 100 % korrekt. Es könnte ja sein, dass du zufällig eine Folge für $x$ gefunden hast, welche den errechneten Grenzwert hat. Eine andere könnte einen anderen Grenzwert haben. Das Verfahren kannst du trotzdem bedenkenlos anwenden, da es in den von dir betrachteten Fällen zu dem tatsächlichen Grenzwert führt.
Alle Videos zum Thema
Videos zum Thema
Grenzwerte x gegen xₒ (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grenzwerte x gegen xₒ (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter







 Grenzwerte von Funktionen für x → xₒ – Testeinsetzung
Grenzwerte von Funktionen für x → xₒ – Testeinsetzung
 Grenzwerte von Funktionen für x → xₒ – Termumformung
Grenzwerte von Funktionen für x → xₒ – Termumformung
 Grenzwerte von Funktionen für x → xₒ – h-Methode
Grenzwerte von Funktionen für x → xₒ – h-Methode









