Zuordnungen und Funktionen

Inhaltsverzeichnis zum Thema

• Was ist eine Funktion?
• Zuordnungen
• Funktionen
• Funktionsgleichung und Funktionsterm
• Der Definitionsbereich und der Wertebereich einer Funktion
• Der Definitionsbereich
• Der Wertebereich
• Eigenschaften von Funktionen

Was ist eine Funktion?

Um diese Frage zu beantworten, schauen wir uns zuerst an, was eine Zuordnung ist.

Zuordnungen

Bei einer Zuordnung werden Größen aus einem Bereich und Größen aus einem anderen Bereich in Beziehung zueinander gestellt.

Dies kennst du eventuell bereits von proportionalen oder antiproportionalen Zuordnungen.

Um genauer zu beschreiben, was eine Zuordnung ist, siehst du nun ein Beispiel. In der Abbildung siehst du die Zuordnung von Schülerinnen und Schülern einer Klasse auf der linken Seite und deren Geschwistern auf der rechten Seite.

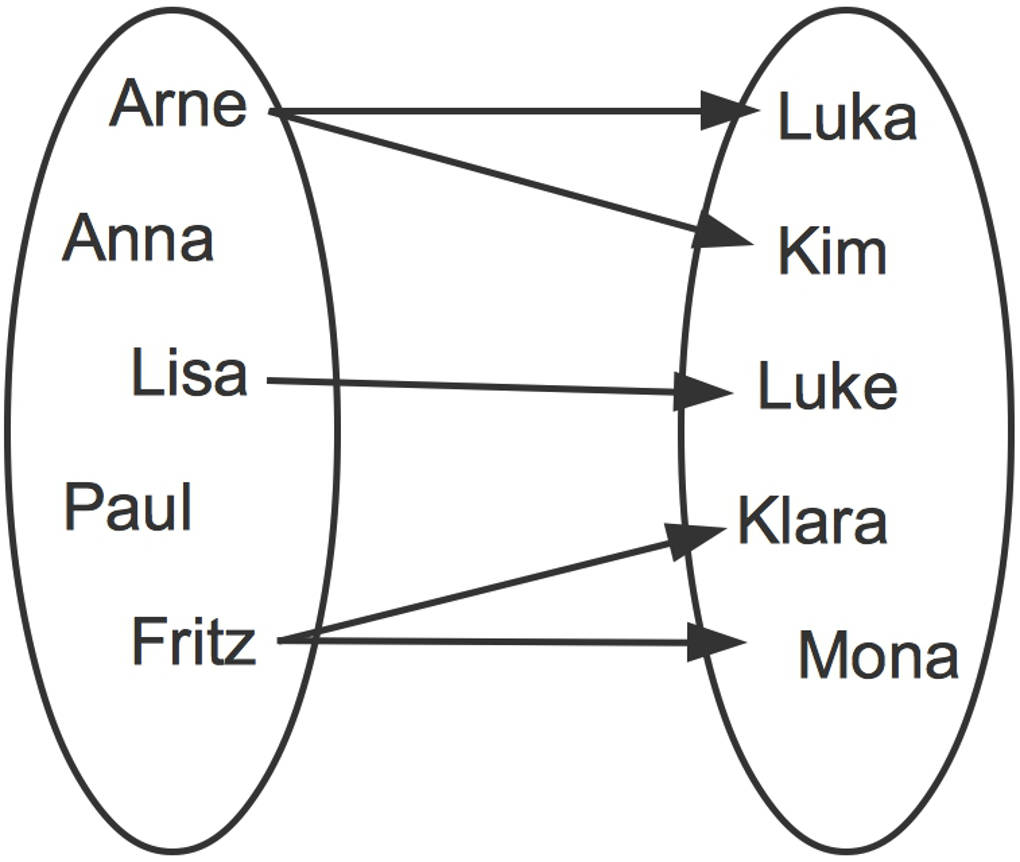
Wir definieren folgende Begriffe:

• Der Definitionsbereich der Zuordnung ist die Menge der Personen links.
• Der Wertebereich ist die Menge der Geschwister rechts.

Das Pfeildiagramm stellt die Zuordnung „Schülerinnen und Schüler zu Namen der Geschwister“ dar.

Du kannst beispielsweise erkennen, dass Arne zwei Geschwister, nämlich Luka und Kim, hat. Deshalb führen zwei Pfeile von Arne weg.

Bei einer Zuordnung muss nicht jeder der Größen des einen Bereichs eine Größe des anderen Bereichs zugeordnet sein. Dies erkennst du an Anna und Paul, die jeweils keine Geschwister haben und von denen kein Pfeil wegführt.

Funktionen

Eine Funktion ist nun eine spezielle Zuordnung, bei der jedem Element $x\in\mathbb{D}$ ($\mathbb{D}$ ist der Definitionsbereich) genau ein Element $y\in\mathbb{W}$ ($\mathbb{W}$ ist der Wertebereich) zugeordnet ist. Diese Eigenschaft wird häufig als Eindeutigkeit bezeichnet.

Wenn du bei dem obigen Beispiel jeder Schülerin bzw. jedem Schüler aus der Klasse die Anzahl seiner Geschwister zuordnest, erhältst du dieses Pfeildiagramm.

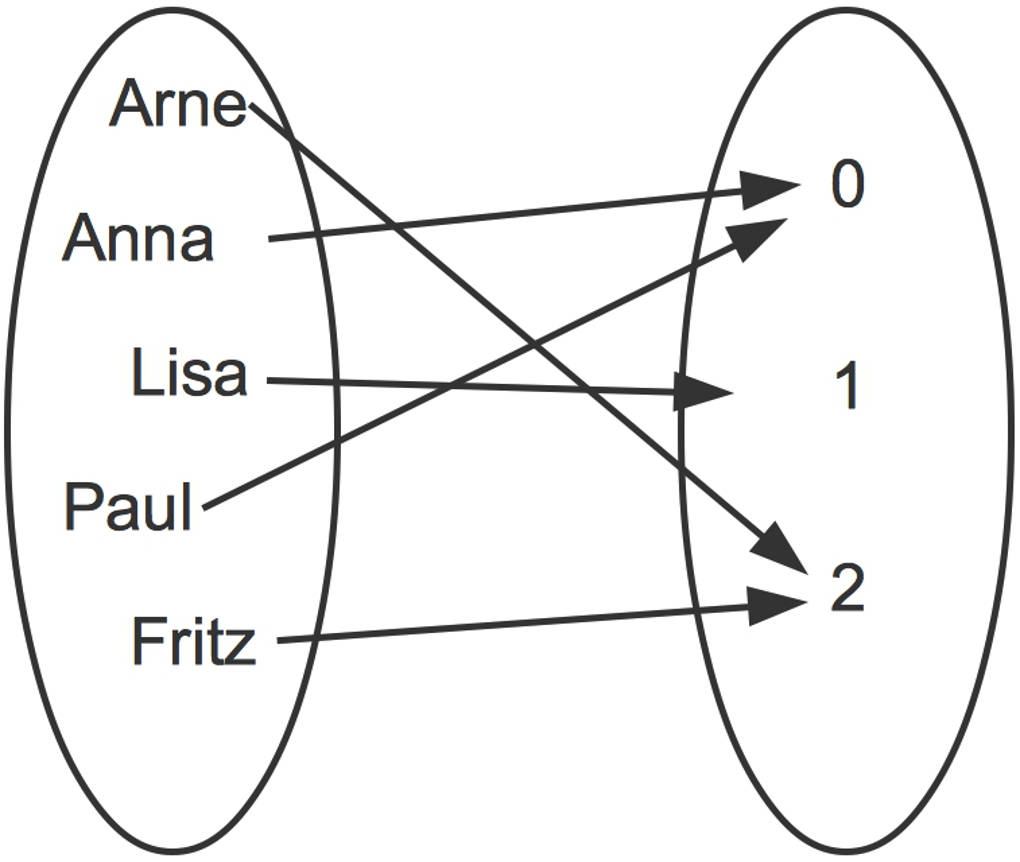
Der Definitionsbereich ist dabei unverändert und enthält alle Personen der Klasse. Der Wertebereich ist nun die Anzahl der Geschwister und wird mit $\{0;1;2\}$ beschrieben.

Hier siehst du, dass von jedem Namen in der linken Menge genau ein (!) Pfeil abgeht. Dies ist die zentrale Eigenschaft, die eine Zuordnung besitzen muss, um eine Funktion zu sein.

Funktionsgleichung und Funktionsterm

Um diese Begriffe zu erklären, schauen wir uns ein weiteres Beispiel an. Dieses mal beinhalten sowohl Definitions- als auch Wertebereich Zahlen.

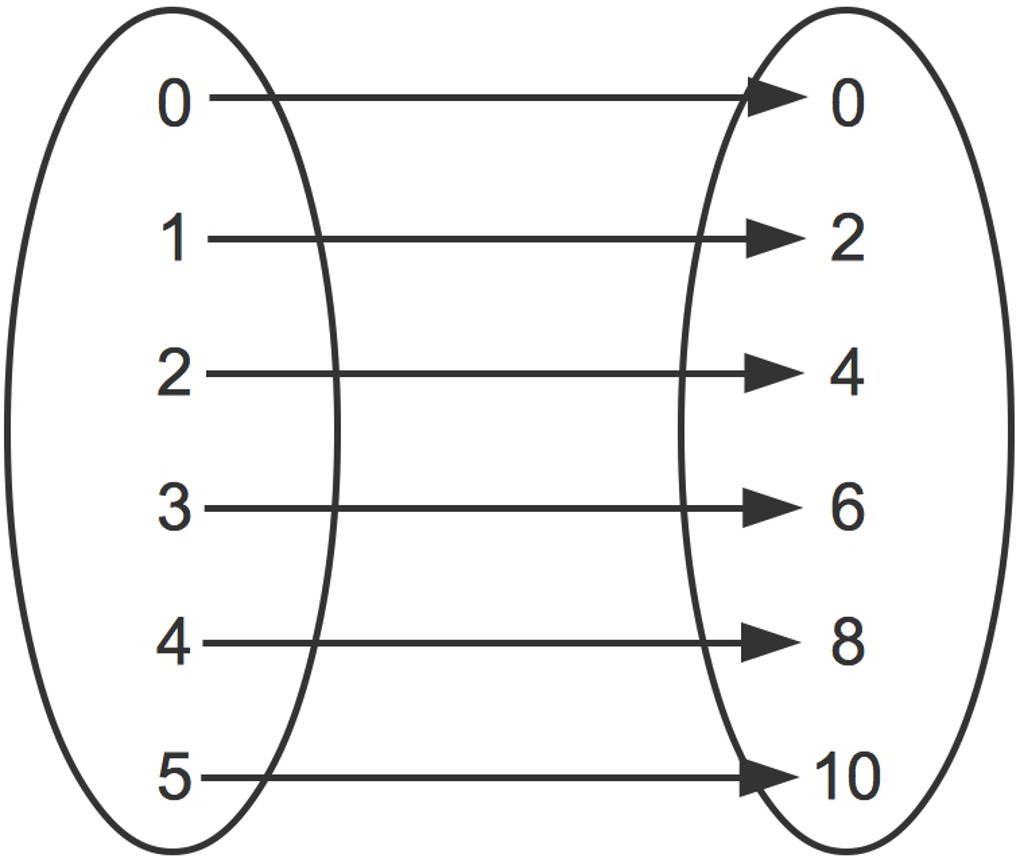
Fällt dir etwas auf? Jeder Zahl in dem linken Bereich wird das Doppelte dieser Zahl zugeordnet. Da von jeder Zahl im Definitionsbereich nur ein Pfeil abgeht, liegt hier eine Funktion vor.

Du kannst diese Zuordnung auch in Form einer Funktionsgleichung ausdrücken. Diese lautet hier $f(x)=2\cdot x$. Dabei gelten folgende Bezeichnungen:

• $f$ ist der Name der Funktion.
• $x$ ist die unabhängige Variable (auch Argument genannt) der Funktion.
• $y=f(x)$ ist die abhängige Variable (auch Funktionswert genannt).
• Der Term rechts vom Gleichheitszeichen wird als Funktionsterm bezeichnet.

Weitere mögliche Darstellungsformen von Funktionen sind beispielsweise Wertetabellen oder Funktionsgraphen.

Der Definitionsbereich und der Wertebereich einer Funktion

Häufig musst du eine Funktion im Rahmen einer sogenannten Kurvendiskussion auf ihren Definitions- und Wertebereich hin untersuchen.

Der Definitionsbereich

in Der Definitionsbereich ist die Menge aller Zahlen, welche du für $x$ die Funktionsgleichung einsetzen darfst. Wir gehen im Folgenden immer von den reellen Zahlen $\mathbb{R}$ als Grundmenge aus.

• Bei der Funktion $f$ mit $f(x)=2\cdot x$ darfst du für $x$ jede reelle Zahl einsetzen. Es ist also $\mathbb{D}=\mathbb{R}$.
• Schau dir nun die Funktion $f$ mit $f(x)=\sqrt x-2$ an. Die Wurzel ist in $\mathbb{R}$ nur für positive Zahlen und $0$ definiert. Somit ist $\mathbb{D}=\mathbb{R}^+_0$. Dabei ist $\mathbb{R}^+_0$ die Menge aller positiven rationalen Zahlen und $0$.
• Bei der Funktion $f(x) = \frac{1}{x}$ darfst du jede reelle Zahl außer der $0$ einsetzen. Es gilt $\mathbb{D} = \mathbb{R}\setminus\{0\}$.

Der Wertebereich

Der Wertebereich ist die Menge aller Zahlen, die als Funktionswerte angenommen werden.

• Sei $f$ mit $f(x)=2\cdot x$ gegeben, dann wird jede reelle Zahl als Wert angenommen. Es ist dann $\mathbb{W}=\mathbb{R}$.
• Bei der quadratischen Funktion $f$ mit $f(x)=x^{2}$ erhältst du nur Werte größer oder gleich $0$. Damit ist $\mathbb{W}=\mathbb{R}^+_0$.

Eigenschaften von Funktionen

Wir schauen uns diese am Beispiel der Funktion $f$ mit $f(x)=x^{3}-3x^{2}+4$ an. Den zugehörigen Funktionsgraphen siehst du hier. Hinweis: Diese Funktion gehört zu den ganzrationalen, kubischen Funktionen. Diese sind üblicherweise Inhalt der zehnten Klasse.

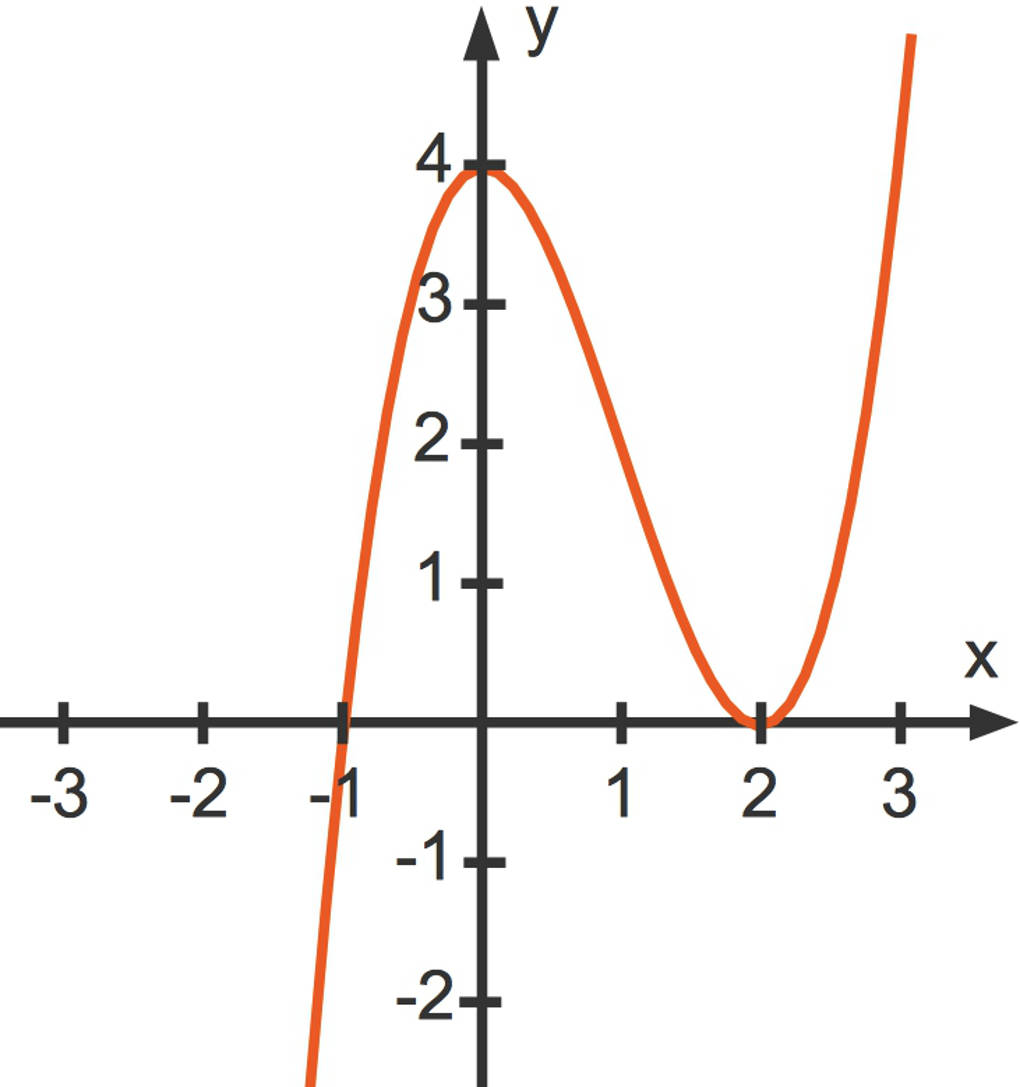
Der hier abgebildete Funktionsgraph ist die grafische Darstellung der Funktion.

• Der Funktionsgraph schneidet die $x$-Achse bei $x=-1$ und bei $x=2$. Diese Stellen werden Nullstellen genannt.
• Der Funktionsgraph schneidet die $y$-Achse bei $y=4$. Dies ist der $y$-Achsenabschnitt.
• In dem Punkt $(0|4)$ hat die Funktion einen lokalen Hochpunkt. Was bedeutet das? Wenn du die Funktionswerte in einem Bereich links von $x=0$ und in einem Bereich rechts von $x=0$ betrachtest, sind diese kleiner als $f(0)=4$.
• Der Punkt $(2|0)$ ist dementsprechend ein lokaler Tiefpunkt. Hier gilt, dass die Funktionswerte in einem Bereich links und rechts von $x=2$ größer sind als $f(2)=0$.
• Du kannst auch erkennen, dass der Funktionsgraph für $x<0$ steigend, für $0<x<2$ fallend="" und="" für="" $x="">2$ wieder steigend ist.</x<2$>