Sinussatz und Cosinussatz
Mit Sinussatz und Cosinussatz kannst du Winkel oder Seitenlängen in einem allgemeinen Dreieck berechnen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Dreiecke
Hier siehst du ein allgemeines Dreieck:
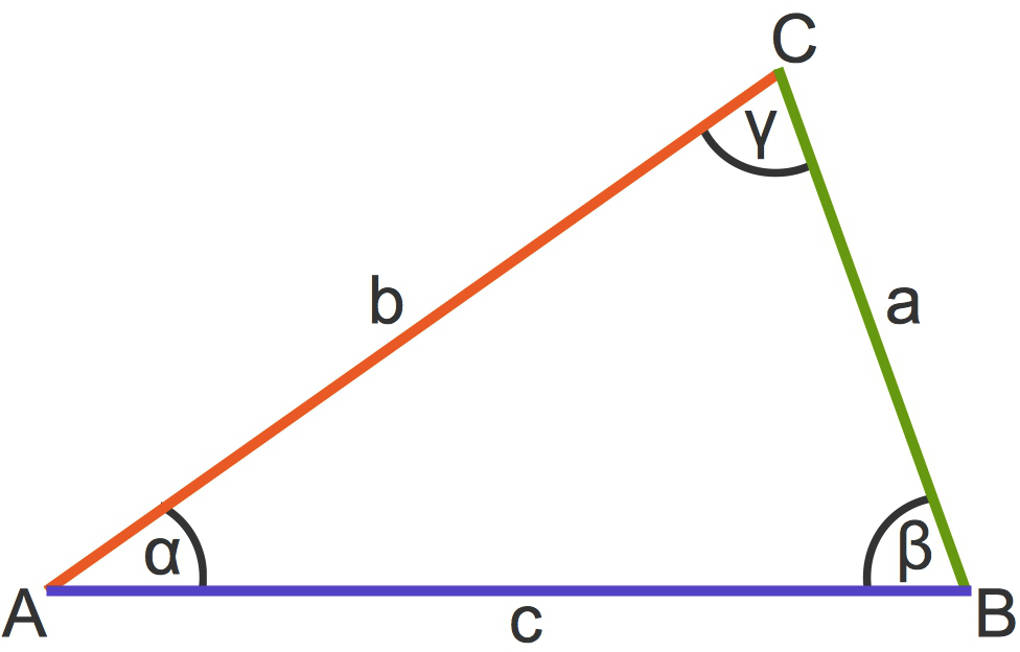
Die Eckpunkte sind mit Großbuchstaben gegen den Uhrzeigersinn bezeichnet, die gegenüberliegenden Seiten werden mit dem entsprechenden Kleinbuchstaben gekennzeichnet und die drei Winkel sind zu erkennen an den griechischen Buchstaben $\alpha$ (alpha) für a, $\beta$ (beta) für b und $\gamma$ (gamma) für $c$.
Es gibt spezielle Dreiecke:
- rechtwinklige Dreiecke - das Dreieck hat einen rechten Winkel ($90^\circ$)
- gleichschenklige Dreiecke - zwei Seiten des Dreiecks sind gleich lang
- gleichseitige Dreiecke - alle drei Seiten des Dreiecks sind gleich lang
In diesen Dreiecken kannst du mit Hilfe des Satzes von Pythagoras oder den trigonometrischen Funktionen in der Trigonometrie – Sinus ($\sin$), Cosinus ($\cos$, auch als Kosinus bezeichnet) und Tangens ($\tan$) – fehlende Seiten oder Winkel berechnen. Dabei musst du sowohl in gleichschenkligen als auch in gleichseitigen Dreiecken jeweils mit Hilfslinien einzeichnen, so dass rechtwinklige Teildreiecke entstehen.
Trigonometrische Funktionen: Sinus, Cosinus und Tangens
In rechtwinkligen Dreiecken sind die Seitenbezeichnungen folgendermaßen:
- die Gegenkathete von $\alpha$ ist die Kathete, die dem spitzen Winkel $\alpha$ gegenüber liegt
- die Ankathete von $\alpha$ ist die Kathete, die dem Winkel $\alpha$ anliegt
- die Hypotenuse ist stets die längste Seite im Dreieck und liegt dem rechten Winkel gegenüber
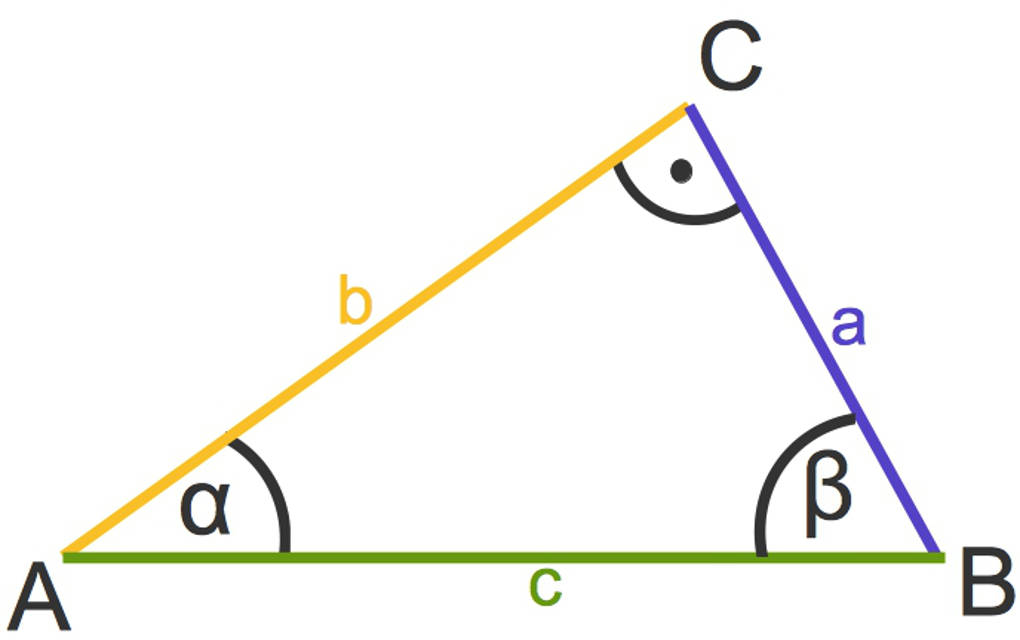
Die trigonometrischen Funktionen in einem rechtwinkligen Dreieck sind wie folgt definiert:
$\sin(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Hypotenuse}}$
$\cos(\alpha)=\frac{\text{Ankathete von }\alpha}{\text{Hypotenuse}}$
$\tan(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Ankathete von }\alpha}$
In allgemeinen Dreiecken sind weder diese Definitionen, noch der Satz des Pythagoras direkt anwendbar.
Sinussatz
Der Sinussatz gibt eine Beziehung zwischen den Winkeln eines allgemeinen Dreiecks und den gegenüberliegenden Seiten an.
Es gilt
$\large{\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}}$
Der Sinussatz kann auch mit den jeweiligen Kehrwerten formuliert werden:
$\large{\frac{\sin(\alpha)}a=\frac{\sin(\beta)}b=\frac{\sin(\gamma)}c}$
Das bedeutet: Wenn du in einem allgemeinen Dreieck von je zwei Winkeln und den entsprechend gegenüberliegenden Seiten drei Größen kennst, kannst die fehlende vierte Größe berechnen.
Beispiel zum Sinussatz
Als Beispiel kannst du den Kongruenzsatz „WSW“ betrachten. Dieser besagt, dass zwei Dreiecke kongruent (deckungsgleich) sind, wenn sie in der Länge einer Seite sowie den beiden anliegenden Winkeln übereinstimmen. Gegeben seien
- die Winkel $\alpha=40^\circ$ und $\beta=60^\circ$ sowie
- die Seite $c=6$
Hier können wir die fehlenden Seitenlängen berechnen. Um allerdings den Sinussatz anwenden zu können, musst du zunächst den dritten Winkel $\gamma$ berechnen. Hierfür verwendest du den Winkelsummensatz für Dreiecke, nach dem die Summe der drei Innenwinkel eines beliebigen Dreiecks immer $180^\circ$ beträgt. Somit ist $40^\circ+60^\circ+\gamma=180^\circ$. Nun kannst du $100^\circ$ subtrahieren und erhältst $\gamma=80^\circ$.
Es gilt also mit den nun bekannten Größen:
$\large{\frac{a}{\sin(40^\circ)}=\frac{6}{\sin(80^\circ)}}$
Du siehst, es ist in dieser Gleichung nur eine Größe unbekannt, nämlich $a$. Multiplikation mit $\sin(40^\circ)$ führt zu
$a=\frac6{\sin(80^\circ)}\cdot \sin(40^\circ)\approx 3,9$
Ebenso kannst du die Länge der Seite $b$ berechnen:
$b=\frac6{\sin(80^\circ)}\cdot \sin(60^\circ)\approx 5,3$
Sinussatz im rechtwinkligen Dreieck
In einem rechtwinkligen Dreieck, mit zum Beispiel $\gamma=90^\circ$ und somit der Hypotenuse $c$, erhältst du
$\large{\frac{\sin(\alpha)}a=\frac{\sin(90^\circ)}c}$
Da $\sin(90^\circ)=1$ ist, kommst du durch Einsetzen und Multiplikation mit $a$ zu
$\sin(\alpha)=\frac ac$
Dies ist die oben bereits angegebene Definition des Sinus in einem rechtwinkligen Dreieck.
Cosinussatz
Der Cosinussatz (auch: Kosinussatz) beschreibt eine Gleichung, in welcher die drei Seiten eines allgemeinen Dreiecks vorkommen sowie der Cosinus eines Winkels.
Es gilt
$a^2=b^2+c^2-2\cdot b\cdot c\cdot \cos(\alpha)$
$b^2=a^2+c^2-2\cdot a\cdot c\cdot \cos(\beta)$
$c^2=a^2+b^2-2\cdot a\cdot b\cdot \cos(\gamma)$
Du kannst dir den Cosinussatz wie folgt merken:
- Auf der linken Seite steht jeweils das Quadrat einer Seite.
- Auf der rechten Seite kommt der Cosinus des Winkels vor, der dieser Seite gegenüberliegt.
- Auf der rechten Seite werden die beiden übrigen Seiten quadriert und die Quadrate addiert. Kommt dir das bekannt vor?
- Von dieser Summe wird das doppelte Produkt der beiden Seiten und dem Cosinus des gegenüber liegenden Winkels abgezogen.
Wenn Seiten quadriert und addiert werden, erinnert dich das sicher an den Satz des Pythagoras. Dieser ist ein besonderer Fall des Cosinussatzes.
Sei zum Beispiel $\gamma=90^\circ$, dann ist $\cos(\gamma)=\cos(90^\circ)=0$. Damit gilt mit der unteren der drei Gleichungen
$c^2=a^2+b^2$
Dies ist gerade der Satz des Pythagoras mit $\gamma=90^\circ$ und der Hypotenuse $c$.
Beispiel zum Cosinussatz
Mit der Anwendung des Cosinussatzes kannst du zum Beispiel bei dem Kongruenzsatz „SWS“ die Länge der fehlenden Seite berechnen. Dieser Kongruenzsatz besagt, dass zwei Dreiecke kongruent sind, wenn sie in zwei Seitenlängen sowie dem von diesen Seiten eingeschlossenen Winkel übereinstimmen. Es seien
- $a=5$ und $b=7$ sowie
- $\gamma=35^\circ$
Zunächst überlegst du dir, welche Größen bekannt sind und welche der drei Gleichungen du verwendest. In diesem Fall kannst du die dritte Gleichung verwenden. In dieser setzt du die bekannten Größen ein.
$c^2=5^2+7^2-2\cdot 5\cdot 7\cdot \cos(35^\circ)\approx 16,66$
Zuletzt ziehst du die Wurzel und erhältst $c\approx 4,1$.
Alle Videos zum Thema
Videos zum Thema
Sinussatz und Cosinussatz (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Sinussatz und Cosinussatz (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter






 Sinussatz – Erklärung und Herleitung
Sinussatz – Erklärung und Herleitung
 Sinussatz und Cosinussatz – Übungen
Sinussatz und Cosinussatz – Übungen









