Volumen und Oberfläche von Zylindern
Über die Grundfläche, die Deckfläche, die Mantelfläche bzw. die Höhe des Zylinders lassen sich sowohl das Volumen als auch die Oberfläche schnell berechnen. Das Körpernetz eines Zylinders ist also ein wichtiges Hilfsmittel.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Zylinder
- Das Volumen eines Zylinders
- Die Mantelfläche eines Zylinders
- Die Oberfläche eines Zylinders
Was ist ein Zylinder
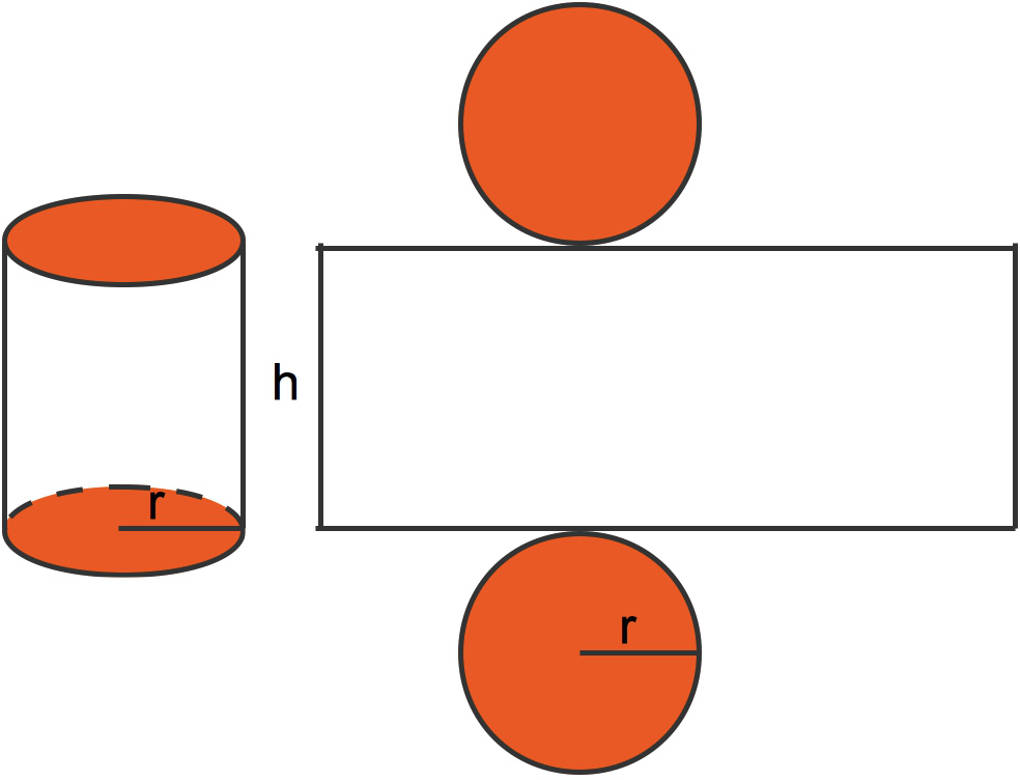
Ein Zylinder wird aus drei Flächen zusammengesetzt:
- Eine Fläche hat abgerollt die Form eines Rechtecks und wird Mantel des Kegels genannt.
- Die zwei übrigen Formen sind zwei identische, also gleich große, Kreise, die parallel zueinander liegen. Diese Kreise bilden die Grund- und Deckfläche des Zylinders. Die Kreise haben jeweils den gleichen Radius $r$.
- Die Höhe des Zylinders $h$ ist auch die Länge einer Seite des Mantels.
- Der Umfang des Kreises der Grund- oder Deckfläche ist die Länge der anderen Seite des Mantels.
In der folgenden Abbildung kannst du links das Schrägbild und rechts das Netz eines Zylinders sehen.
Das Volumen eines Zylinders
Das Volumen eines Zylinders lässt sich mit der folgenden Formel berechnen:
$V=\pi\cdot r^2\cdot h$
.
Dies kannst du dir so ähnlich vorstellen wie bei der Berechnung des Volumens eines Prismas oder, als Spezialfall eines Prismas, eines Quaders.
Du legst auf die Grundfläche des Zylinders Einheitsquadrate, also Quadrate mit den Seitenlängen $1$. Damit kannst du zwar nicht einen Kreis komplett abdecken, du siehst allerdings, dass, ähnlich wie bei einem Prisma oder Quader die Grundfläche schließlich mit der Höhe des Zylinders multipliziert werden muss. Die Formel zur Berechnung des Flächeninhaltes eines Kreises lautet $A=\pi\cdot r^2$, wobei $\pi\approx 3,1415$ die sogenannte Kreiszahl ist.
Beispiel
Eine Getränkedose hat die Form eines Zylinders. Die Grundfläche hat den Radius $r=3,35~cm$. Die Dose ist $11,5~cm$ hoch. Nun kannst du das Volumen, also das Fassungsvermögen der Flasche berechnen.
$V=\pi(3,35~cm)^2\cdot (11,5~cm)=129,06\cdot \pi~cm^3\approx405,45~cm^3$

Üblicherweise werden in Getränkedosen Flüssigkeiten gefüllt. Diese werden in $L$ für Liter oder $cL$ für Zentiliter angegeben. Hierfür musst du dir merken, dass $1000~cm^3 =1~dm^3$ gerade einem Liter entsprechen. Die Dose hätte also ein Fassungsvermögen von ungefähr $0,405~L$. Durch die Stabilität gebende Wölbung des Boden- und Deckelrandes und anderen Beschränkungen wird die Dose jedoch normiert nur mit $0,33~L$ befüllt.
Die Mantelfläche eines Zylinders
Da der Mantel eines Zylinders ein Rechteck ist, lässt sich dessen Flächeninhalt mit der Flächenformel für Rechtecke berechnen.
- Die eine Seite des Rechtecks ist die Höhe $h$ des Zylinders,
- die andere ist der Umfang der Grundfläche.
Dies kannst Du Dir klarmachen, indem du eine Küchenrolle der Länge nach aufschneidest. Nun kannst du den Mantel aufklappen und siehst so zum einen, dass er rechteckig ist, und zum anderen die Seitenlängen des Rechtecks.
Die Formel zur Berechnung des Umfangs eines Kreises lautet $U=2\cdot \pi\cdot r$.
Damit kann auch die Mantelfläche berechnet werden:
$M=2\cdot \pi\cdot r\cdot h$
.
Beispiel
Schaue dir noch einmal das Beispiel der Dose an: Der Hersteller möchte eine Folie um die Dose kleben, auf welcher das Fassungsvermögen, der Name, die Inhaltsstoffe, ... stehen. Wie groß ist diese Folie. Hier wird nach der Mantelfläche gefragt:
$M=2\cdot\pi\cdot (3,35~cm)\cdot (11,5~cm)=77,0\cdot\pi~cm^2\approx 242,6~cm^2$
.
Die Folie hat also eine Fläche von ungefähr $243~cm^2$.
Die Oberfläche eines Zylinders
Die Oberfläche eines Zylinders besteht aus
- der Mantelfläche und
- zweimal der Grundfläche, hierfür verwendest du wieder die Formel für den Flächeninhalt eines Kreises $A=\pi\cdot r^2$.
- Schließlich müssen diese Flächen addiert werden.
Damit kannst du die Oberfläche wie folgt berechnen:
$O=2\cdot \pi\cdot r\cdot h+2\cdot \pi\cdot r^2=2\cdot \pi\cdot r\cdot (h+r)$
.
Ein etwas komplexeres Beispiel zum Schluss

Der Hersteller eines beliebten Fertiggerichtes möchte die Dose, in welche dieses Fertiggericht gefüllt wird, neu gestalten.
- Die Höhe der Dose soll $h=12~cm$ sein und
- das Volumen soll $950~cm^3$ betragen.
Nun stellt sich der Hersteller die folgenden Fragen:
- Wie groß ist der Materialaufwand (in $cm^2$), ohne Verschnitt, zur Herstellung der Dose?
- Wie groß (in $cm^2$) ist der Aufkleber, welcher die gesamte Dose umhüllt? Auf diesem soll das wunderbare Logo der Firma zu sehen sein.
Zuerst überlegst du dir, wonach gefragt ist?
- Der Materialaufwand ist die gesamte Oberfläche.
- Die Größe des Aufklebers entspricht der Mantelfläche.
Da du die Mantelfläche auch für die Oberfläche benötigst, berechnest du erst einmal die Mantelfläche $M=2\cdot \pi\cdot r\cdot h$.
Die Höhe der Dose kennst du bereits, allerdings nicht den Radius der Grundfläche. Diesen kannst du allerdings mit dem bekannten Volumen berechnen:
$\begin{array}{rclll} 950&=&\pi\cdot r^2\cdot 12&|&:\pi~:12\\ \frac{950}{12\pi}&=&r^2\\ 25,2&\approx&r^2&|&\sqrt{~~~}\\ r&\approx&5\end{array}$
Der Radius beträgt somit ungefähr $5~cm$. Diesen kannst du schließlich in der Formel für die Mantelfläche einsetzen:
$M=2\cdot \pi\cdot (5~cm)\cdot (12~cm)=120~\pi~cm^2\approx377~cm^2$
.
Der Aufkleber mit dem Logo des Herstellers hat somit einen Flächeninhalt von $377~cm^2$.
Ebenso kannst du die Oberfläche berechnen
$O=2\cdot \pi\cdot (5~cm)\cdot (12~cm+5~cm)=170~\pi~cm^2\approx 534~cm^2$
.
Der gesamte Materialaufwand zur Herstellung einer Dose beträgt somit $534~cm^2$.
Alle Videos zum Thema
Videos zum Thema
Volumen und Oberfläche von Zylindern (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Volumen und Oberfläche von Zylindern (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen





 Zylinder – Volumen und Oberfläche
Zylinder – Volumen und Oberfläche
 Volumen von Zylindern
Volumen von Zylindern









