Achsenspiegelung
Wenn du morgens in den Spiegeln schaust, siehst du, dass deine linke Gesichtshälfte ziemlich genau so aussieht wie die linke. Dein Gesicht ist annähernd symmetrisch zu einer Achse, welche durch deine Nasenspitze verläuft.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist eine Achsenspiegelung?
Eine Achsenspiegelung ist eine Kongruenzabbildung. Das bedeutet, dass sowohl die Form als auch die Größe von geometrischen Figuren bei einer Achsenspiegelung gleich bleiben.
Du benötigst für eine Achsenspiegelung eine Spiegelachse.
Achsenspiegelung eines Punktes
Hier siehst du, wie eine Achsenspiegelung eines Punktes $P$ durchgeführt wird.
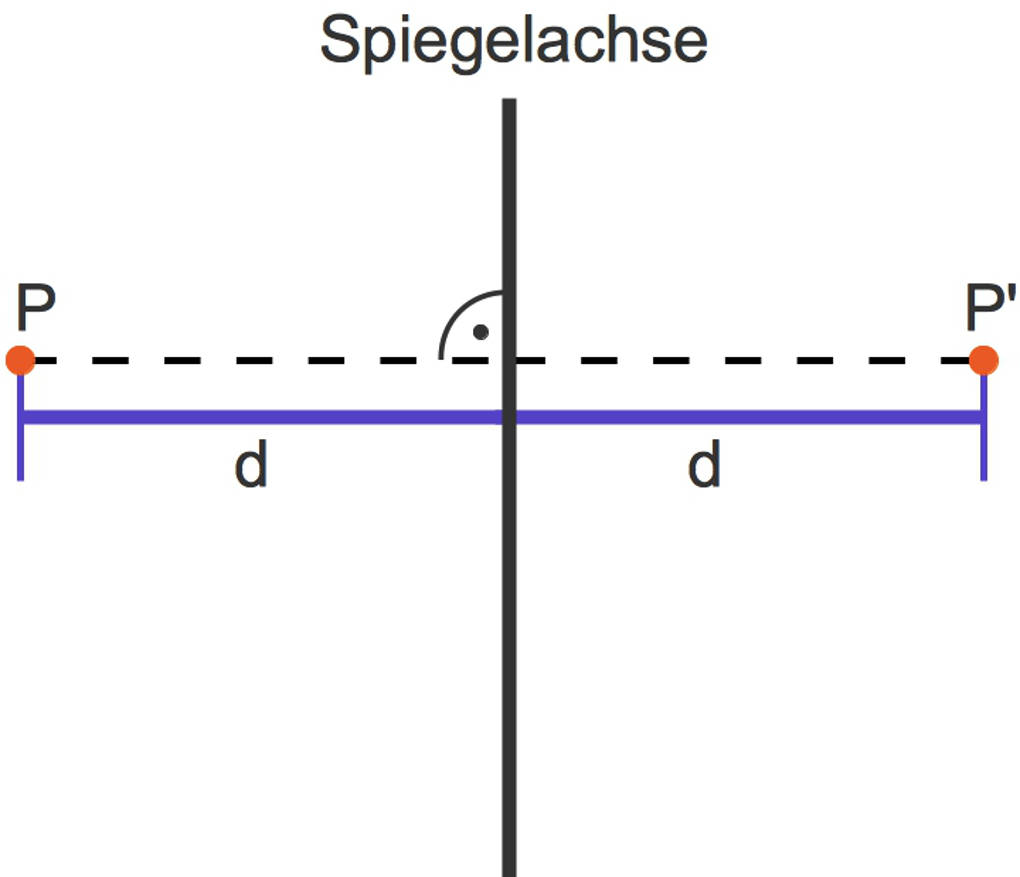
- Der Punkt $P$ soll an der Spiegelachse gespiegelt werden.
- Zunächst zeichnest du eine Linie, die von $P$ ausgehend senkrecht zu der Spiegelachse steht. Also im rechten Winkel zueinander stehen. Diese senkrechte Linie zur Spiegelachse zeichnest du über die Spiegelachse hinaus.
- Nun misst du den Abstand $d$ von Punkt $P$ zu der Spiegelachse.
- Diesen Abstand $d$ misst du auf der gegenüberliegenden Seite der Spiegelachse an der neuen Linie nochmals ab.
- Der Bildpunkt $P'$ des Originalpunktes $P$ entspricht dem Punkt auf der Linie mit dem gemessen Abstand zur Spiegelachse.
Achsenspiegelung einer Strecke
Du spiegelst eine Strecke $\overline{PQ}$, indem du die beiden Punkte $P$ und $Q$, so wie beschrieben, an der Spiegelachse spiegelst. So gelangst du zu den Bildpunkten $P'$ und $Q'$. Die Verbindung dieser Bildpunkte ist die an der Spiegelachse gespiegelte Bildstrecke $\overline{P'Q'}$.
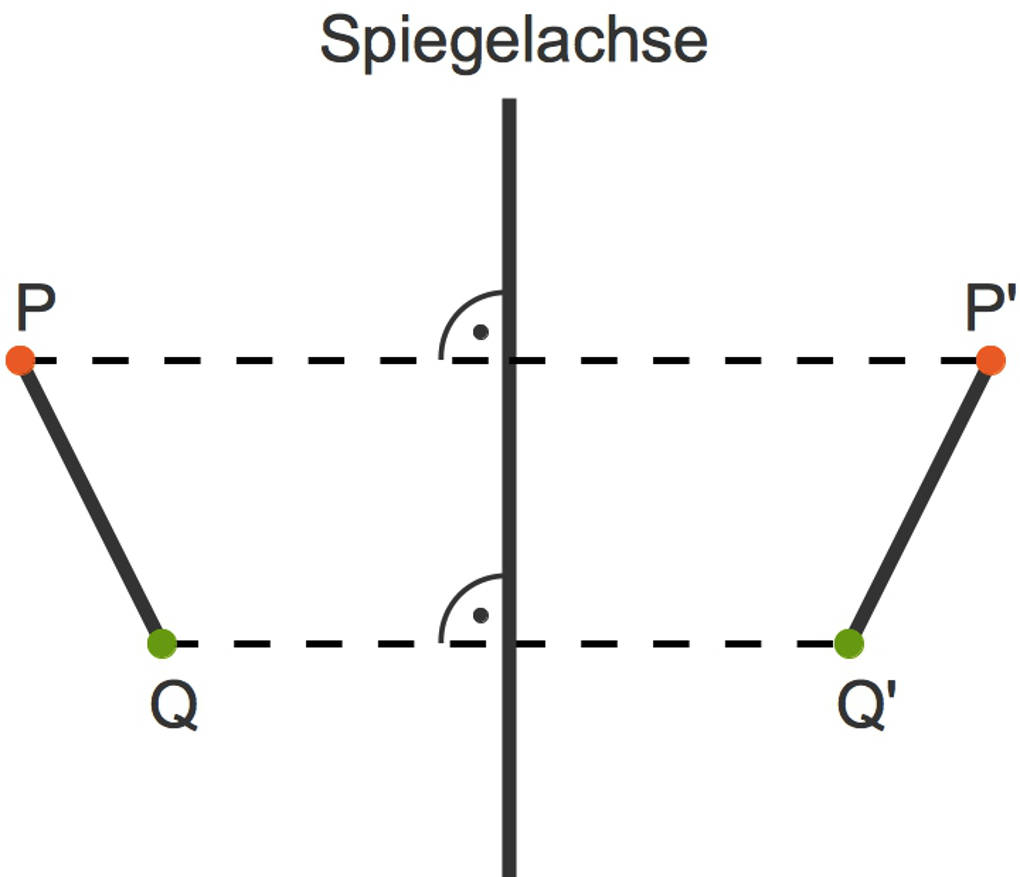
Die Bildstrecke ist ebenso lang wie die Originalstrecke. Das bedeutet, dass die beiden Strecken kongruent sind. „Kongruent“ bedeutet deckungsgleich.
Achsenspiegelung von Vielecken
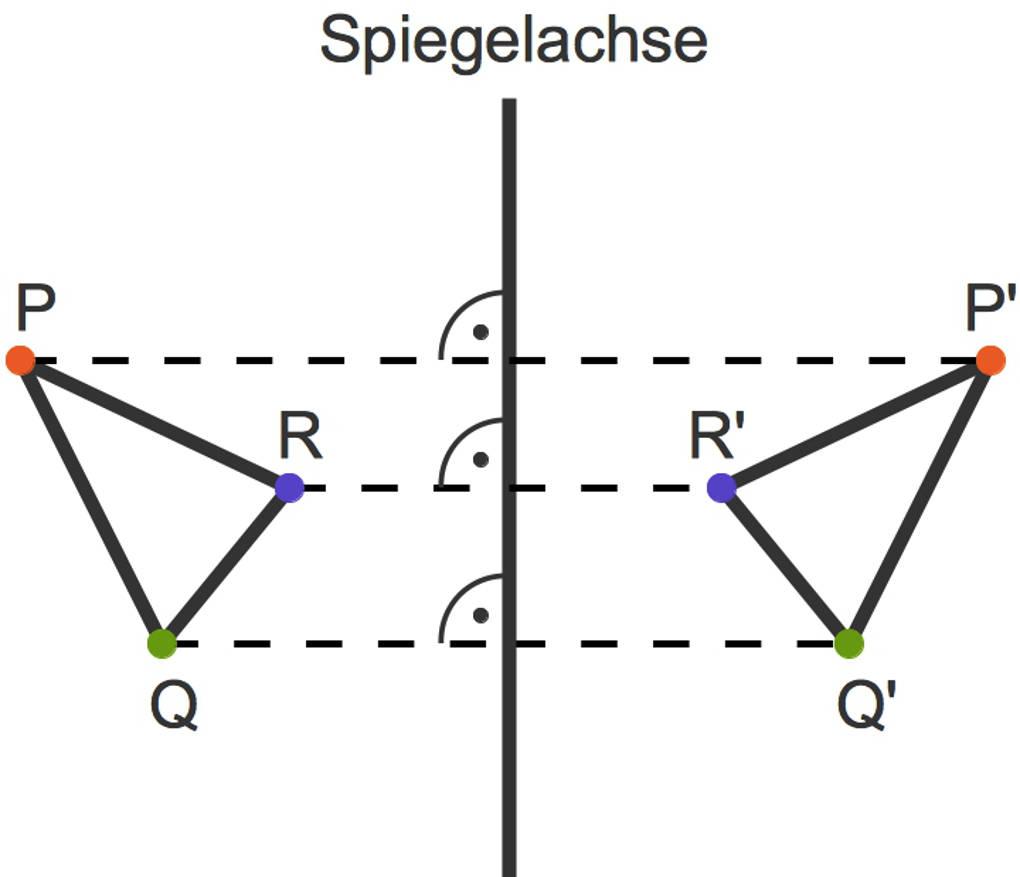
Als Beispiel siehst du hier die Achsenspiegelung eines Dreiecks.
 .
.
- Du spiegelst jeden Eckpunkt des Originaldreiecks, $P$, $Q$ und $R$, wie beschrieben.
- Die durch Spiegelung erhaltenen Bildpunkte $P'$, $Q'$ und $R'$ verbindest du schließlich miteinander zu dem Bilddreieck.
Da alle Seiten des Bilddreiecks ebenso lang sind wie die des Originaldreiecks, sind die beiden Dreiecke kongruent.
Was ist Achsensymmetrie?
Jede Figur, die bei einer Achsenspiegelung in sich selbst übergeht, heißt achsensymmetrisch.
Du kannst dir dies so vorstellen, es gibt eine Achse, welche die Figur halbiert. Wenn du an diese Achse einen Spiegel anlegst, erhältst du mit der halben Figur und dem Spiegelbild wieder die ganze Figur. Diese Achse wird als Symmetrieachse bezeichnet.
Diese Symmetrieachse entspricht der Spiegelachse bei der Achsenspiegelung.
Du kennst sicher einige achsensymmetrische Figuren:
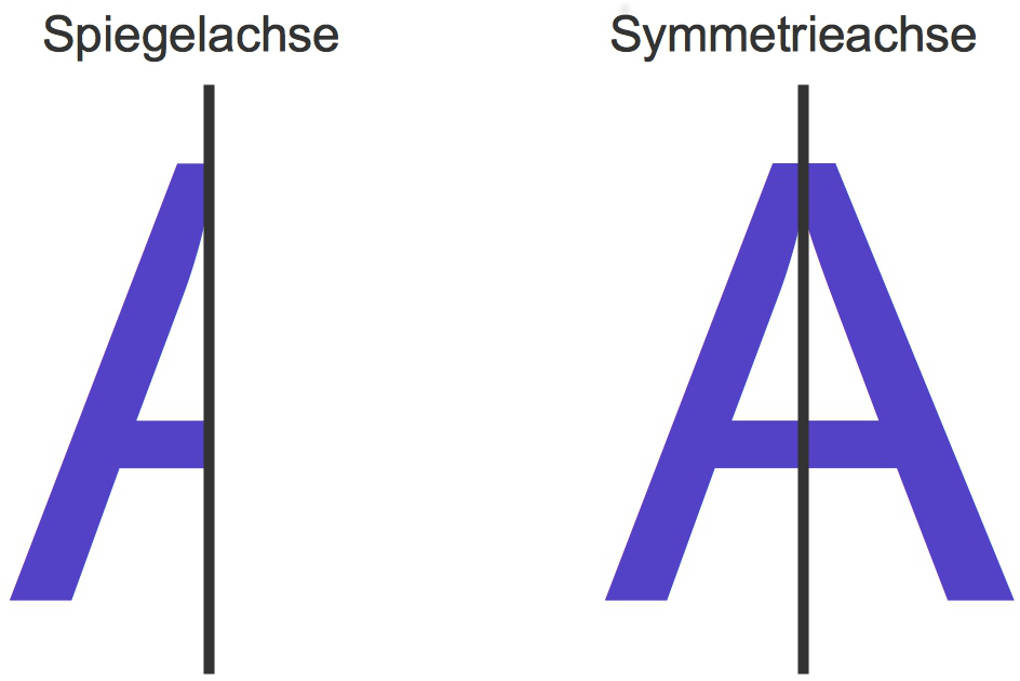
- Wenn du den „halben“ Buchstaben A an der Spiegelachse spiegelst, erhältst du den „ganzen“ Buchstaben A. Das bedeutet, dass dieser Buchstabe achsensymmetrisch ist. Die Symmetrieachse verläuft genau durch die Mitte.
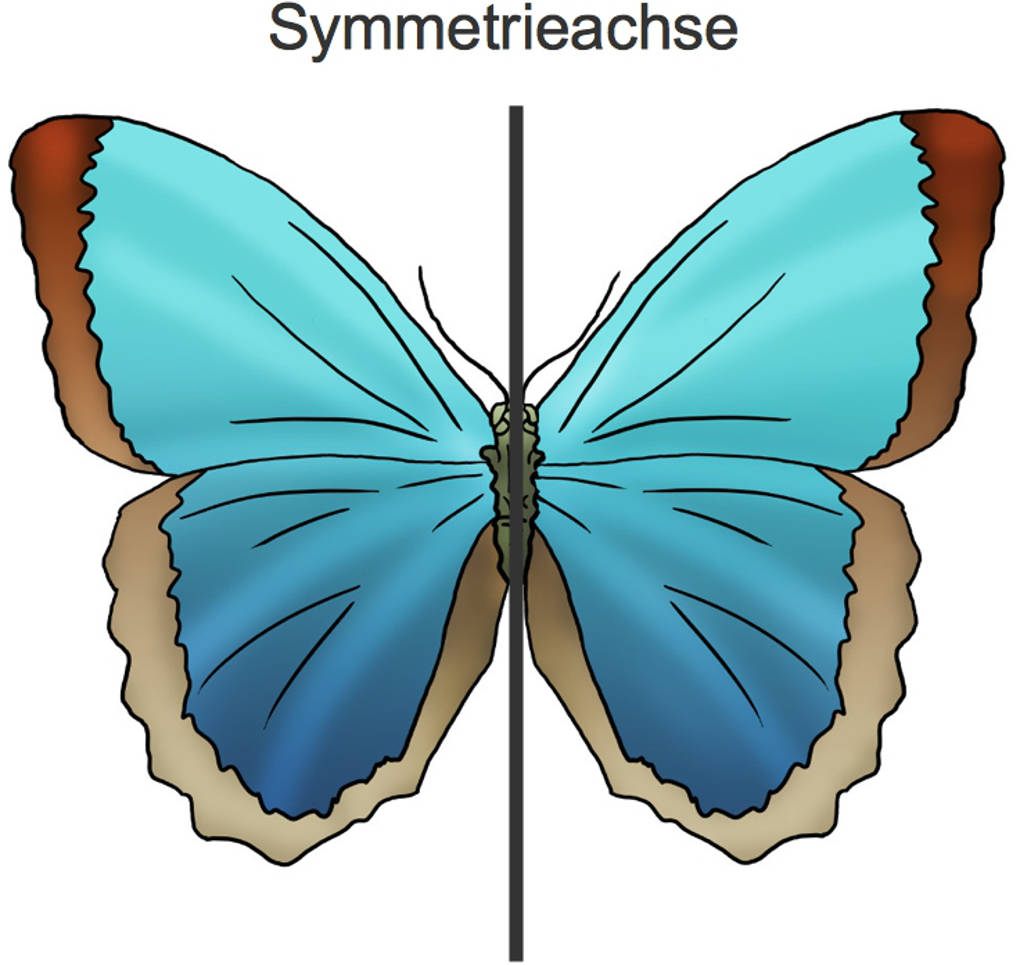
- Ein Schmetterling ist nahezu achsensymmetrisch.
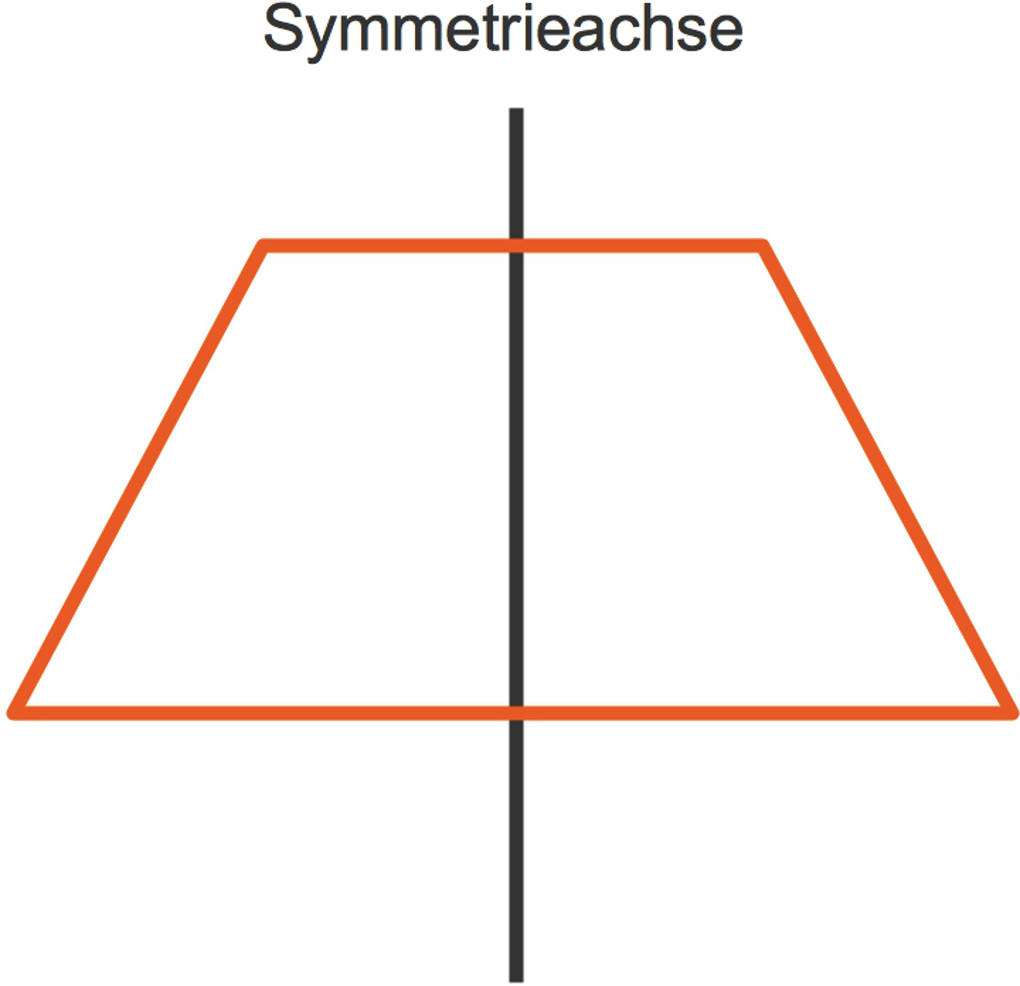
- Ein gleichschenkliges Trapez ist achsensymmetrisch.
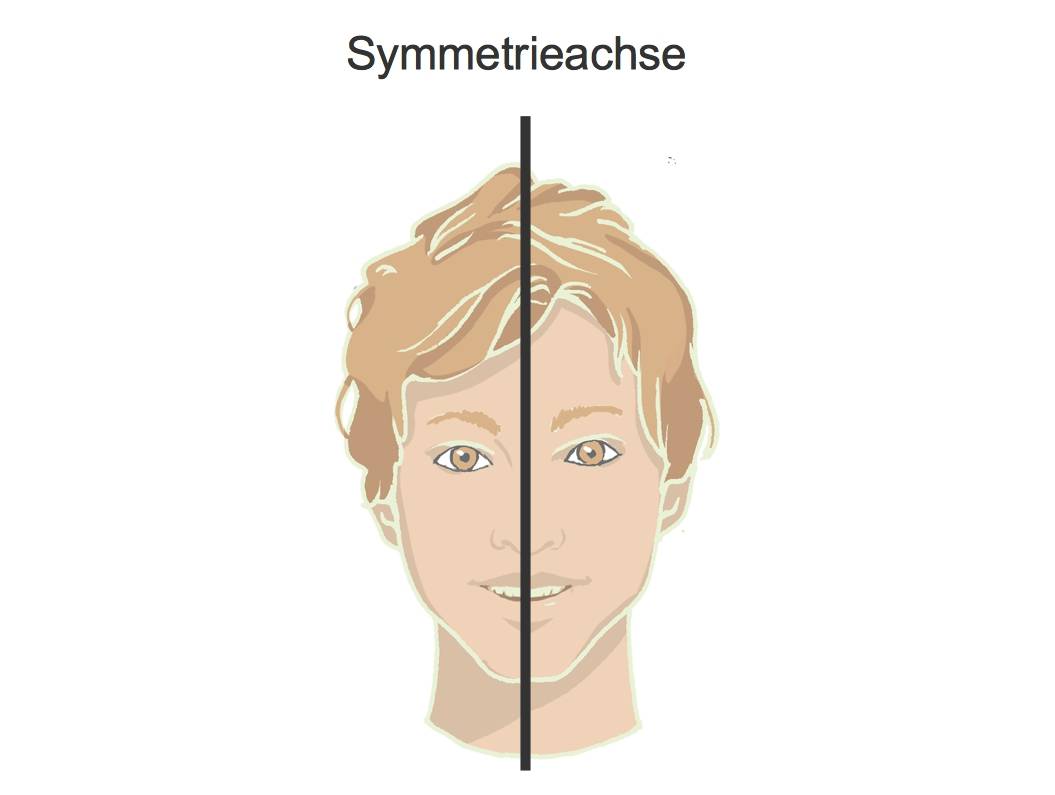
- Dein Gesicht ist auch annähernd achensymmetrisch, bis auf die Frisur.
Achte doch einmal darauf, welche Figuren sind achsensymmetrisch? Du wirst ganz viele solcher Figuren entdecken.
Wie kannst du eine Symmetrieachse finden?
Um festzustellen, ob eine Figur achsensymmetrisch ist, musst du eine Symmetrieachse finden. Anschaulich kannst du eine achsensymmetrische Figur ausschneiden, dann gibt es eine Linie, entlang der du die Figur falten kannst. Du erhältst dann zwei Hälften der Figur, welche sich genau abdecken.
Umgekehrt kannst du ein Blatt Papier falten und ein Muster ausschneiden. Wenn du das Blatt dann wieder auffaltest, hältst du eine achsensymmetrische Figur in der Hand. Die Symmetrieachse ist die Kante, an welcher das Papier gefaltet war.
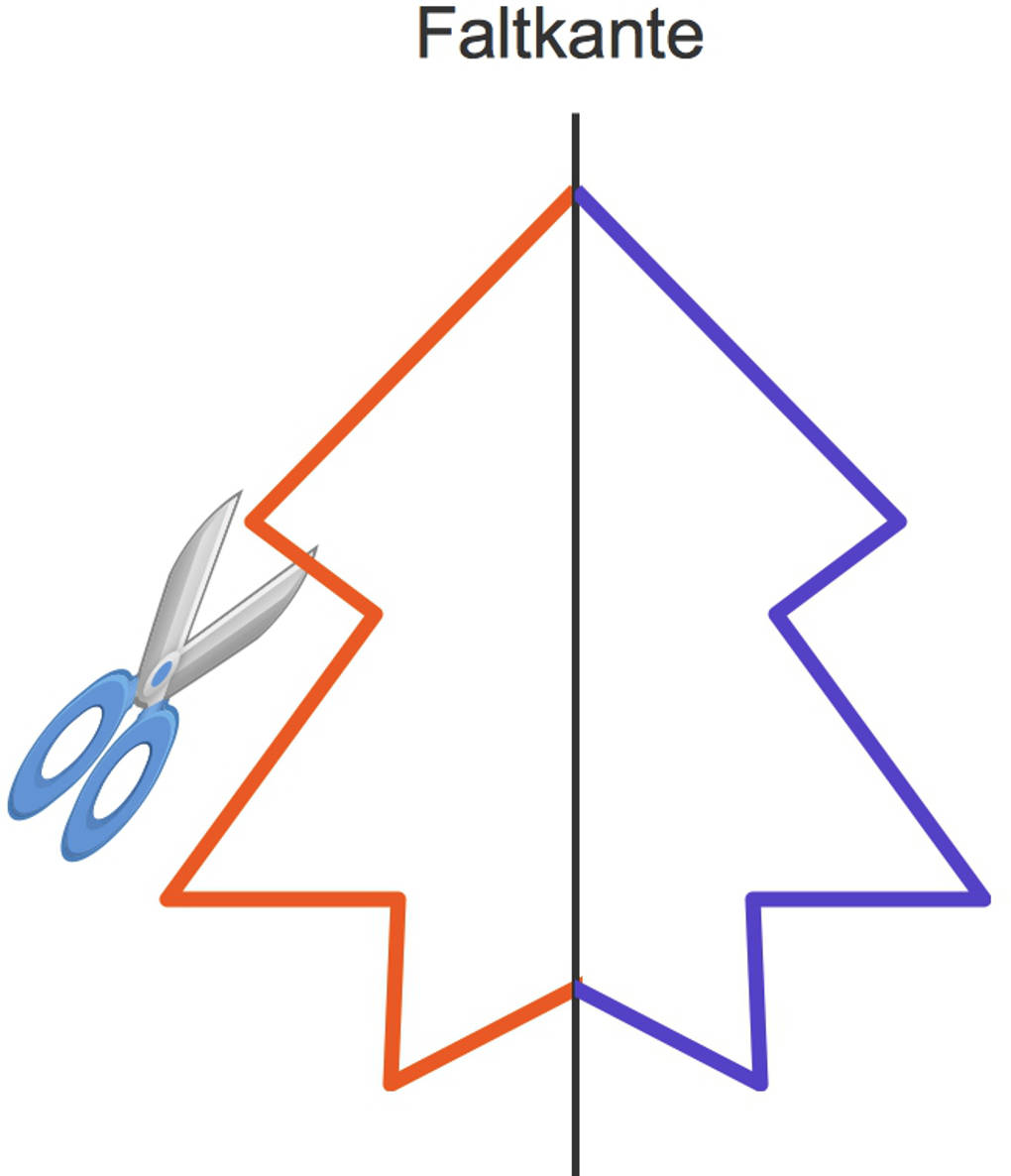
Viel Spaß beim Basteln von achsensymmetrischen Figuren.
Alle Videos zum Thema
Videos zum Thema
Achsenspiegelung (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Achsenspiegelung (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen









 Symmetrieachsen finden
Symmetrieachsen finden
 Achsenspiegelung – Einführung
Achsenspiegelung – Einführung
 Geraden- und Punktspiegelung mit dem Geodreieck – Einführung
Geraden- und Punktspiegelung mit dem Geodreieck – Einführung
 Achsenspiegelung im Koordinatensystem
Achsenspiegelung im Koordinatensystem









