Gegenseitige Lage Kreis-Gerade und Kreis-Kreis

Inhaltsverzeichnis zum Thema

• Kreisgleichung und Geradengleichung
• Die Lage von Geraden und Kreisen zueinander
• Aufstellen einer Tangentengleichung an einen Kreis
• Lage von Kreisen zueinander

Kreisgleichung und Geradengleichung

In der Ebene $\mathbb{R}^{2}$ ist ein Kreis, genauer der Kreisrand, wie folgt gegeben: Auf dem Kreisrand liegen alle Punkte $P(x|y)$, welche den gleichen Abstand zum Mittelpunkt des Kreises $M(m_{x}|m_{y})$ haben. Dieser Abstand ist der Radius $r$ des Kreises.

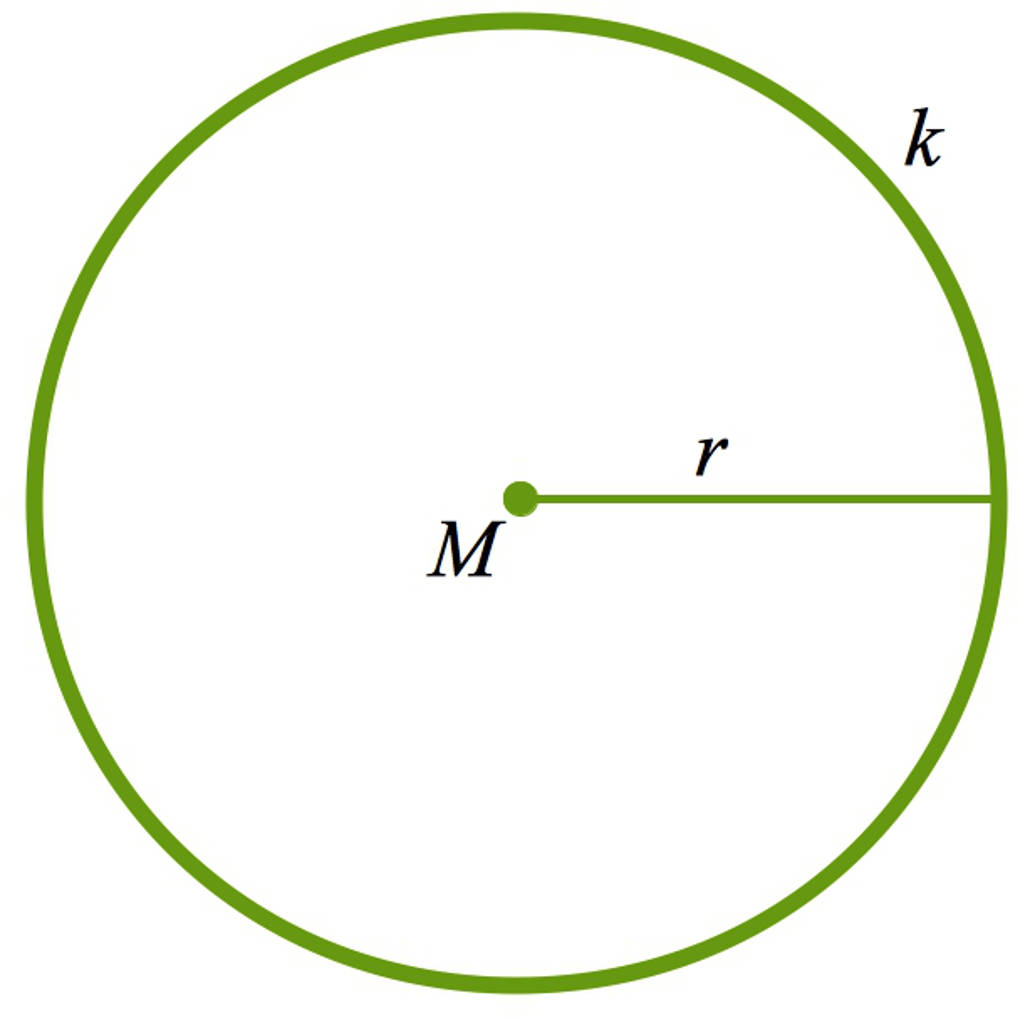
Eine Gerade ist die Lösungsmenge einer linearen Gleichung der Form $ax+by=c$. Dies ist die sogenannte Koordinatengleichung einer Geraden.

Anschaulich kannst du dir drei Lagen einer Gerade zu einem Kreis klarmachen. Diese siehst du in dem folgenden Bild:

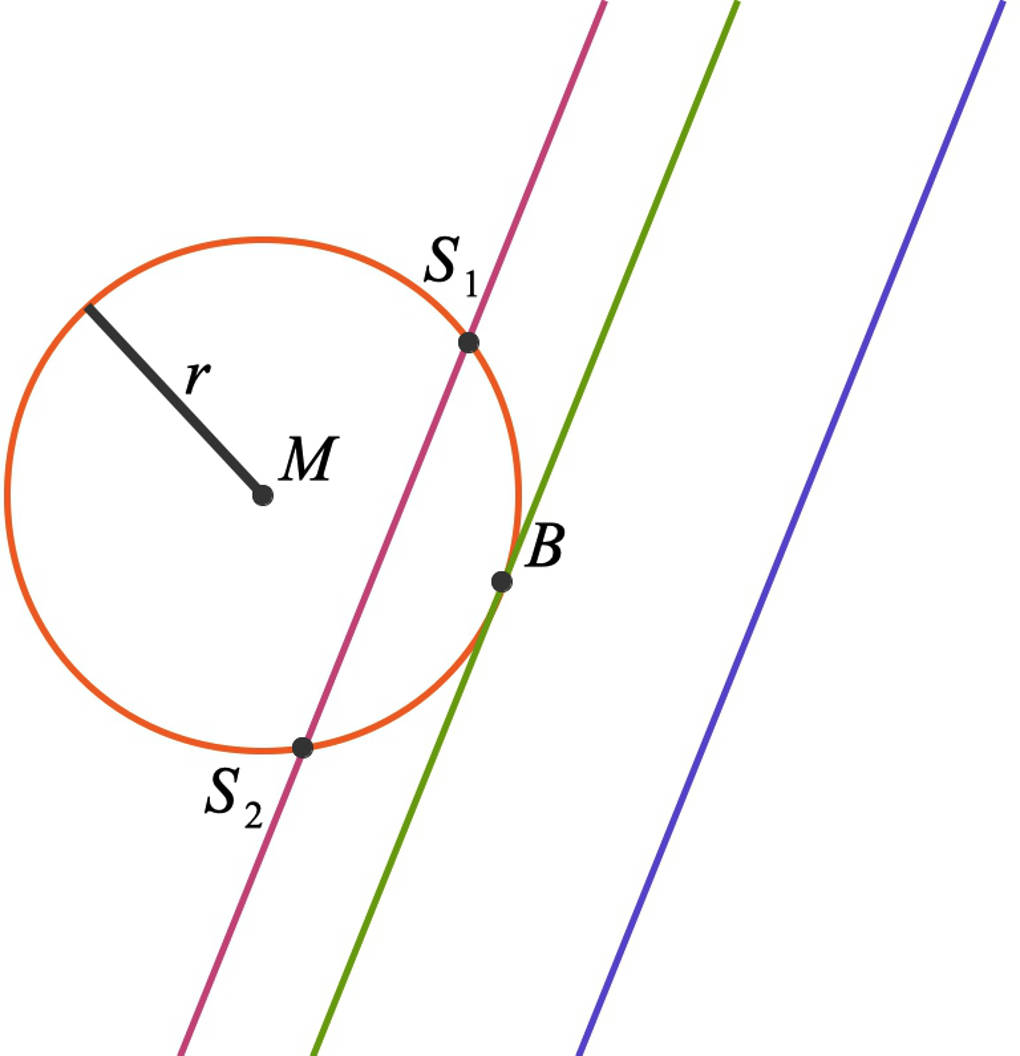
• Die blaue Gerade hat keinen gemeinsamen Punkt mit dem Kreis. Sie geht an diesem vorbei. Daher kommt der Name „Passante“.
• Die grüne Gerade hat einen gemeinsamen Punkt mit dem Kreis. In diesem Punkt $B$ berührt sie den Kreis. „Berühren“ heißt im Lateinischen „tangere“. Diese Gerade heißt „Tangente“.
• Die violette Gerade schließlich schneidet den Kreis in zwei Punkten, $S_{1}$ sowie $S_{2}$. Das lateinische Wort für „schneiden“ ist „secare“. Die Gerade wird als „Sekante“ bezeichnet.

Nun kann es losgehen:

Die Lage von Geraden und Kreisen zueinander

Wir schauen uns den Fall der Schnittpunkte von Geraden und Kreisen an. Gegeben ist ein Kreis mit dem Mittelpunkt $M(2|3)$ sowie dem Radius $r=2$. Dieser Kreis hat die Koordinatengleichung $k:~(x-2)^{2}+(y-3)^{2}=4$.

Auf der linken Seite steht der quadrierte Abstand eines Randpunktes $P(x|y)$ zu dem Mittelpunkt und auf der rechten Seite der quadrierte Radius.

Weiter sei die Gerade $g:~y=x+1$ gegeben. Wie liegt diese Gerade zu dem Kreis $k$?

Du kannst dies überprüfen, indem du in der Kreisgleichung $y$ durch $x+1$ ersetzt:

$(x-2)^{2}+(x+1-3)^{2}=4$

• Wende nun die binomischen Formeln an, um diese Gleichung umzuformen: $x^{2}-4x+4+x^{2}-4x+4=4$.
• Du kannst nun zusammenfassen zu $2x^2-8x+4=0$ oder durch Division durch $2$ zu $x^{2}-4x+2=0$ gelangen.
• Dies ist eine quadratische Gleichung in $x$, welche du mit der p-q-Formel lösen kannst:

$\begin{array}{lll} x_{1;2}&=&2\pm\sqrt{4-2}\\ x_1&=&2+\sqrt2\approx3,41\\ x_2&=&2-\sqrt2\approx0,59 \end{array}$

Nun weißt du bereits, dass es zwei Schnittpunkte gibt. Die Gerade ist somit eine Sekante. Um die Schnittpunkte zu berechnen, setzt du die gefundenen $x$-Werte in die Geradengleichung ein und erhältst $S_{1}(3,41|4,41)$ sowie $S_{2}(0,59|1,59)$.

Die quadratische Gleichung kann auch ...

• ... nur eine Lösung haben. Dann erhältst du einen gemeinsamen Punkt, den Berührpunkt. Die Gerade ist dann eine Tangente.
• ... keine Lösung haben. Es gibt also keine gemeinsamen Punkte. Die Gerade ist eine Passante.

Aufstellen einer Tangentengleichung an einen Kreis

Du kannst übrigens auch zu einem Punkt auf dem Kreisrand die Gleichung einer Tangente aufstellen. Dies siehst du hier an einem Beispiel.

Gegeben sei der Kreis $k:~(x-4)^{2}+(y-1)^{2}=10$. Hier ist $M(4|1)$ der Mittelpunkt und $r=\sqrt{10}$ der Radius des Kreises. Der Punkt $P(1|2)$ liegt auf dem Kreisrand.

Wie kannst du das überprüfen? Setze die Koordinaten von $P$ in die Kreisgleichung ein: $(1-4)^{2}+(2-1)^{2}=(-3)^{2}+1^{2}=10$. Also liegt der Punkt tatsächlich auf dem Kreisrand.

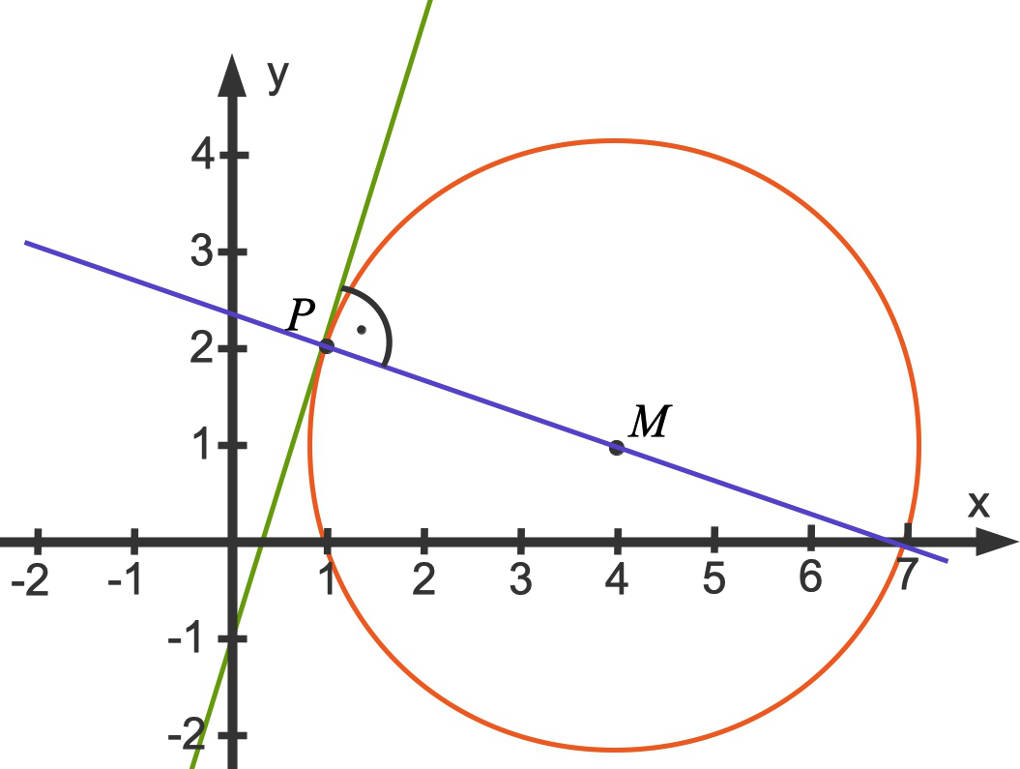
Wie du in diesem Bild sehen kannst, verläuft die grüne Tangente an den Kreis in dem Punkt $P$ senkrecht zu der blauen Geraden durch $P$ und den Mittelpunkt $M$. Die Steigung dieser Geraden durch $P$ und $M$ kannst du so berechnen: Dividiere die Differenz der $y$-Koordinaten durch die der $x$-Koordinaten in der gleichen Reihenfolge:

$m_1=\frac{2-1}{1-4}=-\frac13$

Die Steigung der dazu senkrechten Geraden lässt sich so berechnen:

$m_2=-\frac 1{m_1}=-\frac{1}{-\frac13}=3$

Nun musst du noch den $y$-Achsenabschnitt bestimmen: $2=3\cdot 1+n$. Subtrahiere $3$, so kommst du zu $n=-1$. Die Tangentengleichung lautet also $t:~y=3x-1$.

Lage von Kreisen zueinander

Kommen wir nun zu der Lage zweier Kreise zueinander. Die Unterscheidung erfolgt über die Abstände der Mittelpunkte $M_{1}$ sowie $M_{2}$ der beiden Kreise zueinander sowie die Radien $r_{1}$ und $r_{2}$.

Hier siehst du zum Beispiel zwei sich schneidende Kreise:

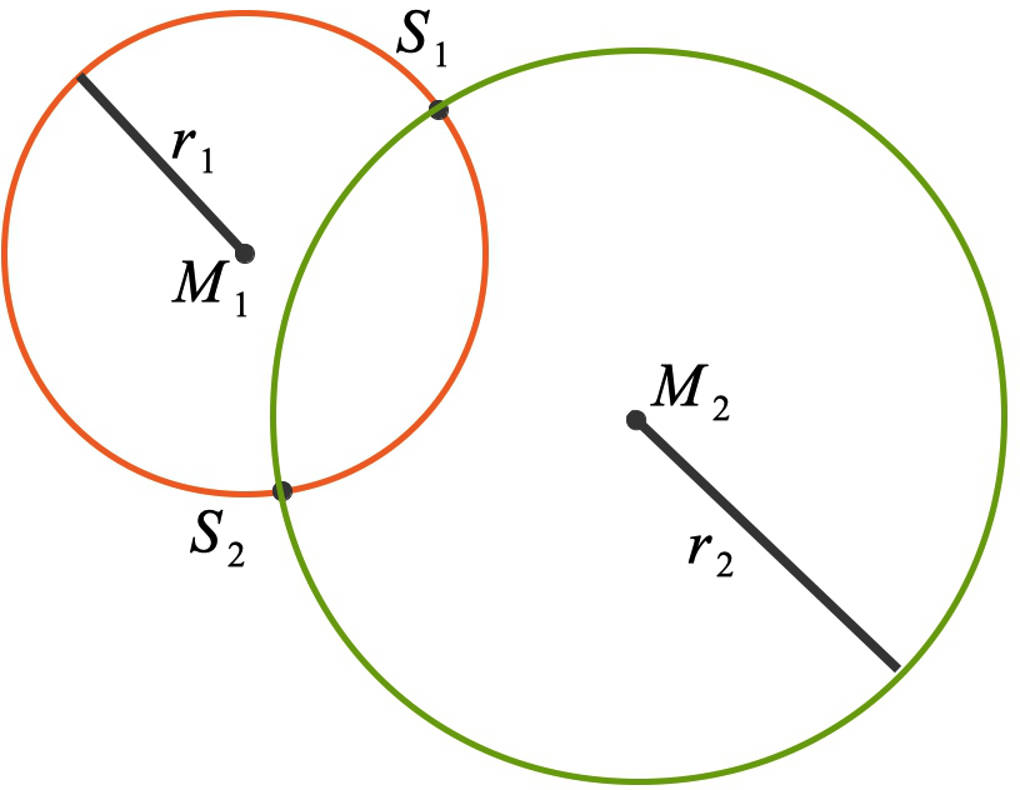
Du berechnest zunächst den Abstand $d$ der beiden Mittelpunkte zueinander und unterscheidest dann die folgenden Fälle, dabei sei $r_{1}\gt r_{2}$:

• $d\gt r_{1}+r_{2}$: Die Kreise berühren sich nicht.
• $d\lt r_{1}-r_{2}$: Der Kreis mit dem kleineren Radius liegt komplett innerhalb des anderen Kreises und berührt diesen nicht.
• $d=r_{1}+r_{2}$: Die Kreise berühren sich von außen.
• $d=r_{1}-r_{2}$: Die Kreise berühren sich von innen.
• In jedem anderen Fall, also $r_{1}-r_{2}\lt d\lt r_{1}+r_{2}$, schneiden sich die Kreise in zwei Punkten.

Dies schauen wir uns abschließend noch an einem Beispiel an:

• $k_{1}:~(x-2)^{2}+(y+1)^{2}=9$ mit $M_{1}(2|-1)$ sowie $r_{1}=3$

• $k_{2}:~(x-1)^{2}+(y-1)^{2}=4$ mit $M_{2}(1|1)$ sowie $r_{2}=2$

• Berechne den Abstand der beiden Mittelpunkte $d=\sqrt{(2-1)^{2}+(-1-1)^{2}}=\sqrt 5$. Es gilt $3-2=1\lt \sqrt 5\lt 5=3+2$. Die beiden Kreise schneiden sich also.

Wende bei beiden Kreisen die binomischen Formeln an:

• $k_{1}:~x^{2}-4x+4+y^{2}+2y+1=9$. Dies kannst du noch umformen zu $k_{1}:~x^{2}-4x+y^{2}+2y=4$.
• $k_{2}:~x^{2}-2x+1+y^{2}-2y+1=4$. Diese Gleichung kannst du umformen zu $k_{2}:~x^{2}-2x+y^{2}-2y=2$.

Subtrahiere nun die beiden Gleichungen:

• So erhältst du $-2x+4y=2$. Subtrahiere noch $4y$ und dividiere durch $-2$.
• Du kommst dann zu der Geradengleichung $x=2y-1$. Diese Gerade hat auch einen speziellen Namen. Das ist die Trägergerade. Auf dieser liegen die beiden Schnittpunkte.
• Setze $x=2y-1$ in $k_{2}$ ein.
• Dies führt zu $4y^{2}-4y+1-4y+2+y^{2}-2y=2$.
• Fasse zusammen zu $5y^{2}-10y+1=0$ und dividiere durch $5$.
• Du erhältst die quadratische Gleichung $y^{2}-2y+0,2=0$ mit den beiden Lösungen:

$\begin{array}{lll} y_{1;2}&=&1\pm\sqrt{1-0,2}\\ y_1&=&1+\sqrt{0,8}\approx1,9\\ y_2&=&1-\sqrt{0,8}\approx0,1 \end{array}$

Nun hast du die Schnittpunkte $S_{1}(1,9|2,8)$ sowie $S_{2}(0,1|-0,8)$ gefunden.