Rechenregeln und Rechengesetze

Inhaltsverzeichnis zum Thema

• Rechenregeln zum Umformen von Termen
• Das Kommutativgesetz
• Das Assoziativgesetz
• Wie du geschickt mit dem Kommutativ- und Assoziativgesetz rechnen kannst.
• Punkt- und Strichrechnung
• Plus- und Minusrechnen
• Malrechnen und Teilen
• Die Regel „Punkt geht vor Strich“
• Beispiele
• Klammern zuerst
• Beispiele

Rechenregeln zum Umformen von Termen

Sowohl das Kommutativgesetz als auch das Assoziativgesetz sind Regeln für das Umformen von Termen.

• Der Name „Kommutativgesetz“ wird von dem lateinischen Verb „commutare“ für „vertauschen“ abgeleitet. Dieses Gesetz ist auch als Vertauschungsgesetz bekannt. Dieses Gesetz besagt, dass die Reihenfolge von Summanden in Summentermen und Faktoren in Produkttermen vertauscht werden kann.
• Auf das lateinische Verb „associare“ für „verbinden“ geht der Name „Assoziativgesetz“ zurück. Du kannst dieses Gesetz auch als Verbindungsgesetz bezeichnen. Dieses Gesetz besagt, dass in Summentermen und in Produkttermen Klammern beliebig gesetzt oder auch weggelassen werden dürfen.

Das Kommutativgesetz

Das Kommutativgesetz der Addition besagt, dass die Reihenfolge beim Addieren vertauscht werden darf:

• 2 + 3 = 3 + 2 = 5
• 13 + 24 = 24 + 13 = 37

Wieso ist das so? Du kannst dir das so klarmachen:

Bei 3 roten und 2 grünen Quadraten erkennst du, dass es egal ist, ob du zu den 3 roten Quadraten 2 grüne zufügst oder umgekehrt. Du erhältst beide Male 5 Quadrate. Du kannst dir das auch an einem Zahlenstrahl klar machen:

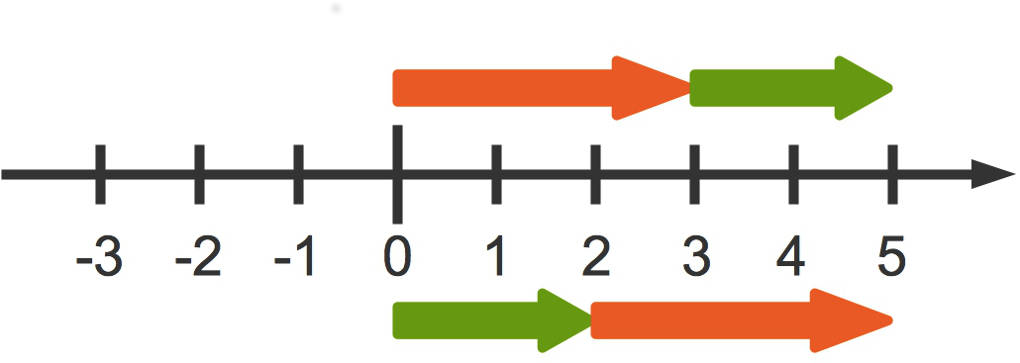
Wenn du zunächst 3 Schritte nach rechts gehst und dann noch einmal 2 Schritte, landest du bei insgesamt 5 Schritten nach rechts. Wenn du aber zunächst 2 Schritte nach rechts gehst und dann noch einmal 3 Schritte, bist du insgesamt ebenfalls 5 Schritte nach rechts gegangen. Der mathematische Ausdruck für das Kommutativgesetz der Addition lautet:

a+b=b+a.

Das Kommutativgesetz gilt auch für die Multiplikation:

• 2 $\cdot$ 3 = 3 $\cdot$ 2 = 6
• 2 $\cdot$ 4 = 4 $\cdot$ 12 = 48

Auch dies kannst du dir anschaulich klar machen. Dafür betrachten wir wieder das obere der beiden Beispiele an einem Zahlenstrahl. Die beiden roten Pfeile stehen für 2 $\cdot$ 3 und die drei grünen für 3 $\cdot$ 2. Du siehst, das Ergebnis ist beide Male 6.

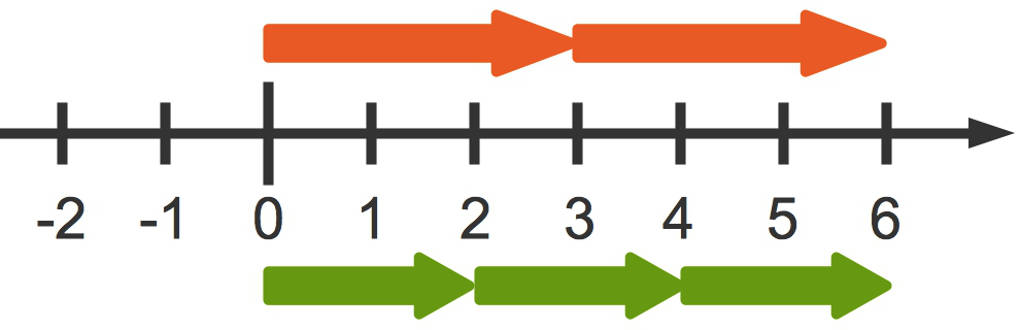
Der Rechenausdruck sieht so ähnlich aus wie der bei der Addition. Das Operationszeichen ist diesmal ein Multiplikationszeichen.

a $\cdot$ b = b $\cdot$ a

Beachte: Das Kommutativgesetz gilt nicht bei der Subtraktion oder bei der Division, wie die folgenden Beispiele zeigen.

• 4 - 2 = 2 aber 2 - 4 = -2
• 8 : 4 = 2 aber 4 : 8 = 0,5

Das Assoziativgesetz

Das Assoziativgesetz gilt ebenfalls für die Addition sowie für die Multiplikation.

a + b + c = ( a + b ) + c = a + ( b + c )

a $\cdot$ b $\cdot$ c = (a $\cdot$ b) $\cdot$ c = a $\cdot$ ( b $\cdot$ c )

Du kannst also die Summanden und Faktoren beliebig miteinander verbinden. Hier siehst du wieder einige Beispiel für das Assoziativgesetz:

• 3 + 2 + 5 = ( 3 + 2 ) + 5 = 5 + 5 = 10 oder

• 3 + 2 + 5 = 3 + ( 2 + 5 ) = 3 + 7 = 10

• 6 $\cdot$ 7 $\cdot$ 5 = 6 $\cdot$ ( 7 $\cdot$ 5 ) = 6 $\cdot$ 35 = 210 oder

• 6 $\cdot$ 7 $\cdot$ 5 = ( 6 $\cdot$ 7) $\cdot$ 5 = 42 $\cdot$ 5 = 210

Das obere Beispiel kannst du dir anschaulich an einem Zahlenstrahl vorstellen. Die beiden Pfeile, die auf der gleichen Höhe stehen, werden jeweils als Erstes gerechnet.

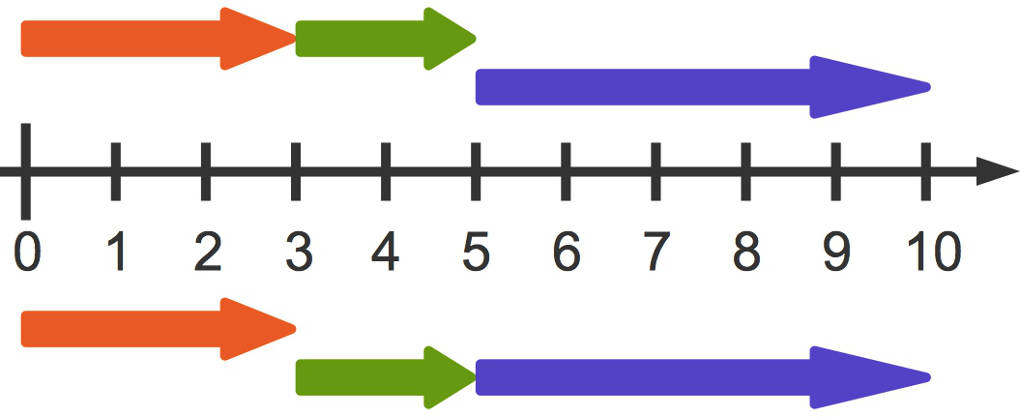
Beachte: Auch das Assoziativgesetz gilt nicht bei der Subtraktion oder bei der Division.

Wie du geschickt mit dem Kommutativ- und Assoziativgesetz rechnen kannst.

Bei den letzten beiden Beispielen ist es vielleicht so, dass dir die eine Art zu rechnen vielleicht besser liegt als die andere. Bei einigen Aufgaben ist es jedoch sinnvoll, die beiden Rechenregeln zu verwenden, um geschickter zu rechnen.

Beispiel: 7 + 8 + 24 + 2 + 13 + 46

Du könntest von links nach rechts rechnen:

$\begin{array}{rcl} 7+8+24+2+13+46&=&15+24+2+13+46\\ &=&39+2+13+46\\ &=&41+13+46\\ &=&54+46\\ &=&100\end{array}$

Durch die Überträge ist das Rechnen etwas kompliziert. Du könntest auch wie folgt vorgehen:

• Vertausche die Reihenfolge so, dass immer zwei Summanden hintereinander stehen, die addiert eine Zehnerzahl ergeben: 7 + 8 + 24 + 2 + 13 + 46 = 7 + 13 + 8 + 2 + 24 + 46. Hierfür verwendest du das Kommutativgesetz.
• Nun verbindest du die Summanden, die addiert eine Zehnerzahl ergeben: 7 + 13 + 8 + 2 + 24 + 46 = ( 7 + 13 ) + ( 8 + 2 ) + ( 24 + 46 ). Dies ist das Assoziativgesetz.
• Rechne die jeweiligen Summen in den Klammern aus: ( 7 + 13 ) + ( 8 + 2 ) + ( 24 + 46 ) = 20 + 10 + 70.
• Zuletzt kannst du noch die Zehnerzahlen addieren und erhältst 20 + 10 + 70 = 100

Punkt- und Strichrechnung

Du lernst recht früh in der Schule das Plusrechnen und das Malrechnen kennen.

Plus- und Minusrechnen

Plusrechnen ist eine Strichrechnung. Statt plusrechnen sagt der Mathematiker auch addieren. Es gibt noch eine weitere Strichrechnung, die Umkehrung des Plusrechnens. Das ist das Minusrechnen. Hier lautet der Fachbegriff subtrahieren.

Schau dir einmal Beispiele an:

• $4+5=9$,
• $13-2=11$.

Beide Rechenzeichen, sowohl das Pluszeichen $(+)$ als auch das Minuszeichen $(-)$, bestehen aus Strichen. So kannst du dir merken, dass es sich bei beiden Rechnungen um Strichrechnungen handelt.

Malrechnen und Teilen

Malrechnen ist eine Punktrechnung. Hier spricht der Mathematiker von der Grundrechenart Multiplikation. Auch bei der Punktrechnung gibt es eine weitere Rechenoperation, nämlich das Teilen oder auch Dividieren.

Schau dir wieder Beispiele an:

• $4\cdot 5=20$,
• $21:3=7$.

Sowohl das Malzeichen $(\cdot)$ für die Multiplikation als auch das Geteiltzeichen $(:)$ für die Division bestehen aus Punkten. Merke dir also, dass es sich bei diesen beiden Rechnungen um Punktrechnungen handelt.

Übrigens: Alle $vier$ Rechenarten werden als Grundrechenarten bezeichnet.

Nun kann es losgehen.

Die Regel „Punkt geht vor Strich“

Üblicherweise rechnest du von links nach rechts.

Zum Beispiel ist $2+3+6+12=5+6+12=11+12=23$. Du addierst also erst die ersten beiden Summanden. Zu dem Ergebnis addierst du dann den dritten und schließlich den vierten Summanden. Das gilt so allerdings nur, wenn du ausschließlich eine Strich- oder eine Punktrechnung hast.

Wenn in einer Aufgabe beide Rechenarten vorkommen, gilt die Regel Punkt vor Strich. Die Punktrechnung hat also Vorrang vor der Strichrechnung.

Wir schauen uns das einmal an folgendem Beispiel an: $3+2\cdot 5$.

• Wenn du von links nach rechts rechnest, erhältst du $3+2\cdot 5=5\cdot 5=25$. Das ist allerdings falsch.
• Du musst zunächst die Punktrechnung durchführen. Du rechnest also $3+2\cdot 5=3+10=13$. So ist das korrekt.

Übrigens: Diese Regel lässt sich nicht begründen. Sie hat sich so durchgesetzt.

Beispiele

Hier siehst du noch weitere Beispiele für die Regel Punkt vor Strich.

1. $12-4\cdot 3$: Rechne zuerst $4\cdot 3=12$ und dann $12-12=0$.
2. $3+7:7-8\cdot 2$: Führe zuerst die beiden Punktrechnungen durch $7:7=1$ und $8\cdot 2=16$. Es folgt dann $3+1-16$. Jetzt rechnest du wieder von links nach rechts $3+1-16=4-16=-12$. Fertig.
3. Die Rechnungen können auch immer länger werden, z.B. $12-2\cdot 3\cdot 4+24:8-12:2\cdot 4=12-24+3-24=-33$.

Klammern zuerst

Kommt in einer Rechnung eine Klammer vor, rechnest du zunächst den Wert für den Term in der Klammer aus. Kurz kannst du auch Klammer zuerst sagen.

Auch hierfür schauen wir uns zunächst ein Beispiel sehr ausführlich an. Du sollst im Folgenden den Wert des Terms $2+3\cdot (4-2)$ berechnen.

1. Berechne zuerst den Wert des Klammerterms $4-2=2$. Die Rechnung lautet jetzt $2+3\cdot 2$.
2. Das kennst du bereits: Du führst als nächstes die Punktrechnung $3\cdot 2=6$ durch und erhältst nun $2+6$.
3. Die Strichrechnung liefert $2+6=8$.

Zusammengefasst sieht das dann so aus: $2+3\cdot (4-2)=2+3\cdot 2=2+6=8$.

Nun kannst du an weiteren Beispielen Klammern zuerst und Punkt vor Strich üben.

Beispiele

1. Beispiel: $(3+4)\cdot (5-2)$

• Berechne erst die Klammerterme $3+4=7$ und $5-2=3$.
• Nun kannst du multiplizieren $7\cdot 3=21$.

2. Beispiel: $7-3\cdot (8-5)+3\cdot 4$

• Auch hier berechnest du erst den Klammerterm $8-5=3$. So kommst du zu $7-3\cdot 3+3\cdot 4$.
• Führe nun die Punktrechnungen $3\cdot 3=9$ sowie $3\cdot 4=12$ durch.
• Schließlich kommt die Strichrechnung $7-9+12=10$.

3. Beispiel: $3\cdot \left(23-2\cdot (2+7)\right)+4\cdot 6$

Die Klammern können also auch verschachtelt sein. Puh, das sieht sehr kompliziert aus. Rechne Schritt für Schritt.

• Es ist $23-2\cdot (2+7)=23-2\cdot 9=23-18=5$. Damit ist die große Klammer schon fertig.
• Nun lautet die Aufgabe $3\cdot 5+4\cdot 6$. Hier musst du zunächst die Punktrechnungen durchführen. Es folgt $15+24$.
• Zuletzt kommt die Strichrechnung mit $15+24=39$.

Viel Spaß beim Üben.