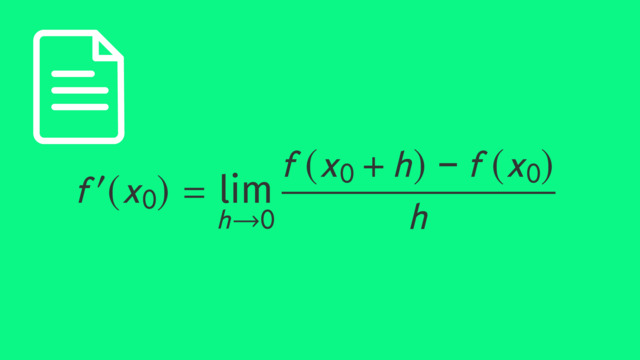Ableitungen der Grundfunktionen mit dem Differenzialquotienten

Ableitungen mit dem Differenzialquotienten – benötigtes Vorwissen

Für dieses Thema solltest du wissen, was der Differenzialquotient ist. Zur Erinnerung:

Außerdem solltest du wissen, wie man den Differenzialquotienten mithilfe der h-Methode bestimmt.

Im Folgenden sollen nun die Ableitungsfunktionen einiger Funktionstypen mithilfe des Differenzialquotienten bestimmt werden. Dies dient der Vermittlung der Funktionsweise von dem Differenzialquotienten und zur Verdeutlichung der Thematik. In der Praxis ist es wesentlich einfacher, Ableitungsfunktionen mit den entsprechenden Ableitungsregeln zu bestimmen.

Ableitung von Potenzfunktionen

Wir beginnen mit den Potenzfunktionen. Das schließt alle Funktionen der folgenden Form ein:

$f(x) = a \cdot x^n, a \neq 0, n \in \mathbb{N}_0$

Ableitung einer Konstanten

Für $n = 0$ erhalten wir die Funktionsgleichung $f(x) = a \cdot x^0 = a$. Diese lässt sich wie folgt mit der h-Methode ableiten:

$\begin{array}{rccl} f'(x_0) & = & \lim\limits_{h \to 0} & \dfrac{f(x_0 + h)~–~f(x_0)}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{a~–~a}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{0}{h} \\ \\ & = & & 0 \\ \end{array}$

Im ersten Umformungsschritt konnten wir für die Funktionswerte $f(x_0+h)$ und $f(x_0)$ jeweils einfach $a$ einsetzen, da $f(x)=a$ gilt. So erhalten wir $0$ für alle Werte von $a$. Dies kann man sich auch anhand des Graphen von $f(x) = a$ deutlich machen, der eine Gerade darstellt, die parallel zur $x$-Achse ist und die $y$-Achse bei $y = a$ schneidet.

Diese Gerade hat tatsächlich überall die Steigung $0$.

Ableitung von $f(x) = a \cdot x$

Für $n = 1$ erhalten wir die Funktionsgleichung $f(x) = a \cdot x¹= a \cdot x$. Diese lässt sich wie folgt mit der h-Methode ableiten:

$\begin{array}{rccl} f'(x_0) & = & \lim\limits_{h \to 0} & \dfrac{f(x_0 + h)~–~f(x_0)}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{a \cdot (x_0 + h)~–~a \cdot x_0}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{ax_0 + ah~–~ax_0}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{ah}{h} \\ \\ & = & & a \\ \end{array}$

Im ersten Schritt setzen wir wieder die Funktionswerte oberhalb des Bruchstrichs ein, dann multiplizieren wir aus und anschließend wird nur noch vereinfacht. Der Ableitungsgraph der Funktion $f(x) = a \cdot x$ ist also eine Konstante, die die $y$-Achse bei $y = a$ schneidet.

Ableitung von $f(x) =a \cdot x^2$

Nun schauen wir uns noch den Fall $n = 2$ an, der repräsentativ für alle weiteren Werte für $n$ gilt. Wir erhalten die Funktionsgleichung $f(x) = a \cdot x^2$ und damit:

$\begin{array}{rccl} f'(x_0) & = & \lim\limits_{h \to 0} & \dfrac{f(x_0 + h)~–~f(x_0)}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{a \cdot (x_0 + h)^2~–~a \cdot x_0^2}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{a \cdot (x_0^2 + 2x_0h + h^2)~–~ax_0^2}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{ax_0^2 + 2ax_0h + ah^2~–~ax_0^2}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{2ax_0h + ah^2}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{h \cdot (2ax_0 + ah)}{h} \\ \\ & = & \lim\limits_{h \to 0} & 2ax_0 + ah \\ \\ & = & & 2ax_0 \\ \end{array}$

In Zeile drei haben wir die erste binomische Formel angewendet, dann vereinfacht, $h$ ausgeklammert und gekürzt. Gemäß der Potenzregel beim Ableiten ist also der Exponent der $x$-Potenz zum Faktor vor dem $x$ geworden und der Exponent hat sich um $1$ verringert.

Ableitung einer gebrochen rationalen Funktion

Auch gebrochen rationale Funktionen lassen sich mithilfe der h-Methode ableiten. Im Folgenden schauen wir uns das anhand der Funktion $f(x) = \frac{1}{x}$ an:

$\begin{array}{rccl} f'(x_0) & = & \lim\limits_{h \to 0} & \dfrac{f(x_0 + h)~–~f(x_0)}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{\frac{1}{x_0 + h}~–~\frac{1}{x_0}}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{\frac{x_0}{(x_0 + h) \cdot x_0}~–~\frac{x_0 + h}{(x_0 + h) \cdot x_0}}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{\frac{x_0~–~(x_0 + h)}{x_0^2 + hx_0}}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{–h}{x_0^2 + hx_0} \cdot \dfrac{1}{h} \\ \\ & = & \lim\limits_{h \to 0} & – \dfrac{1}{x_0^2 + hx_0} \\ \\ & = & & – \dfrac{1}{x_0^2} \\ \end{array}$

Um die Ableitung zu bestimmen, haben wir die Brüche in Zeile drei durch Erweitern gleichnamig gemacht, dann zusammengefasst und dann vereinfacht.

Ableitung einer Wurzelfunktion

Zuletzt wollen wir uns die Ableitung einer Wurzelfunktion mit dem Differenzialquotienten anschauen. Wir betrachten also die Funktion $f(x) = \sqrt{x}$.

$\begin{array}{rccl} f'(x_0) & = & \lim\limits_{h \to 0} & \dfrac{f(x_0 + h)~–~f(x_0)}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{\sqrt{x_0 + h}~–~\sqrt{x_0}}{h} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{(\sqrt{x_0 + h}~–~\sqrt{x_0}) \cdot (\sqrt{x_0 + h}~+~\sqrt{x_0})}{h \cdot (\sqrt{x_0 + h}~+~\sqrt{x_0})} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{x_0 + h~–~x_0}{h \cdot (\sqrt{x_0 + h}~+~\sqrt{x_0})} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{h}{h \cdot (\sqrt{x_0 + h}~+~\sqrt{x_0})} \\ \\ & = & \lim\limits_{h \to 0} & \dfrac{1}{\sqrt{x_0 + h}~+~\sqrt{x_0}} \\ \\ & = & & \dfrac{1}{2 \sqrt{x_0}} \\ \end{array}$

Hier haben wir in Zeile drei den Bruch so erweitert, dass die dritte binomische Formel angewendet werden kann. Anschließend muss nur noch vereinfacht, gekürzt und der Grenzwert betrachtet werden.

Ableitungen mit dem Differenzialquotienten – Zusammenfassung

Mithilfe des Differenzialquotienten und der h-Methode können Funktionsgleichungen abgeleitet werden. Dazu verwendet man folgende Gleichung:

Häufig gestellte Fragen zum Thema Ableitung mit dem Differenzialquotienten