Signifikanztests

Inhaltsverzeichnis zum Thema

• Signifikanztest
• Vorbereitendes
• Einseitiger Signifikanztest - Beispiel
• Sich einen Überblick verschaffen
• Fehler 1. Art berechnen
• Fehler 2. Art berechnen
• Signifikanzniveau
• Zweiseitiger Signifikanztest - Beispiel
• Signifikanzniveau - Beispiel

Signifikanztest

Statistische Testverfahren helfen uns mittels Beobachtungen auf unbekannte Wahrscheinlichkeiten $p$ zu schließen. Im Gegensatz zum Alternativtest wird beim Signifikanztest nicht zwischen zwei Wahrscheinlichkeiten $p_1$ und $p_2$ entschieden. Vielmehr haben wir beim Signifikanztest nur eine Vermutung über $p$, die durch einen statistischen Test entweder bestätigt oder verworfen werden soll. Es gibt ein- und zweiseitige Signifikanztests.

Vorbereitendes

Insgesamt solltest du schon mit Alternativtests und den Fehlerarten (Fehler 1. und 2. Art) vertraut sein und wissen, wie du aus der Tabelle der kumulierten Binomialverteilung Werte abliest. Hier kannst du dir noch einmal die Fehlerarten vergegenwärtigen.

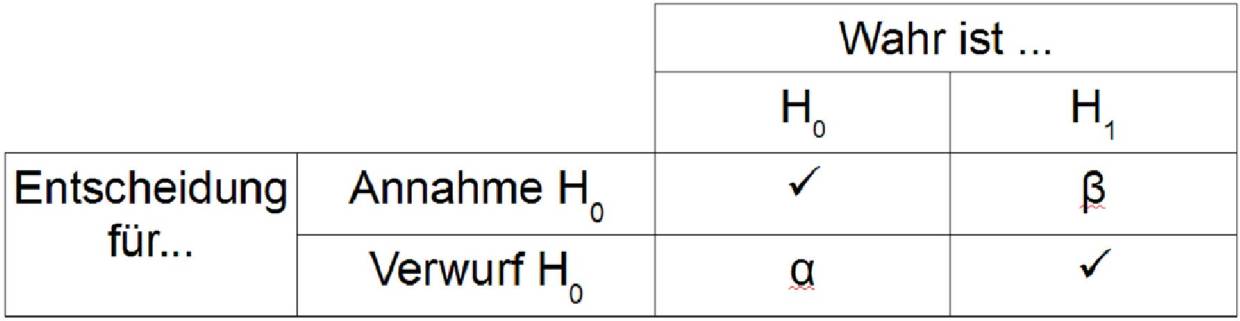
Dabei entspricht der $\alpha$-Fehler dem Fehler 1. Art und der $\beta$-Fehler dem Fehler 2. Art.

Schauen wir uns ein Beispiel für einen einseitigen Signifikanztest an.

Einseitiger Signifikanztest - Beispiel

Eine Pharma-Herstellerin hat viele Jahre an einem neuen Medikament geforscht. Nun möchte sie natürlich auch wissen, wie wirksam es ist. Wo findet sie eine Antwort auf diese Frage?

Das beste vergleichbare Medikament wirkt in $40~\%$ der Fälle. Die Pharma-Herstellerin geht natürlich davon aus, dass ihr Medikament noch häufiger wirkt und legt die Hypothese fest: Mein Medikament ist noch wirksamer ($H_1$). Dazu werden $50$ Probanden ausgewählt und sie sagt:

• Wenn das Medikament bei weniger oder gleich $25$ Probanden wirkt, dann ist mein Medikament nur genauso gut wie das alte.
• Wenn das Medikament bei mehr als $25$ Probanden wirkt, dann ist mein Medikament besser als das alte.

Wir stellen uns nun die entscheidende Frage: Wie hoch ist die Wahrscheinlichkeit, dass die Pharma-Herstellerin ihr Medikament für besser hält, obwohl es nicht besser ist?

Sich einen Überblick verschaffen

Bei Signifikanztests wird es schnell unübersichtlich. Es ist daher sehr wichtig, die Informationen systematisch festzuhalten:

• $n$ ist die Anzahl aller Probanden (Stichprobengröße). $X$ ist die Anzahl der Probanden, bei denen das Medikament wirkt (Prüfgröße). Weil die Prüfgröße ungefähr binomialverteilt ist, können wir im Folgenden die Tabelle zur kumulierten Binomialverteilung verwenden.
• $p$ ist die Wahrscheinlichkeit, dass das neue Medikament wirkt.
• $H_0$ ist die (Null-)Hypothese, dass das neue Medikament genauso gut ist wie das alte. Wir schreiben: $H_0: p=0,4$
• $H_1$ ist die Hypothese, dass das neue Medikament besser ist als das alte. Wir schreiben: $H_1: p \gt 0,4$. Diese Hypothese (die Gegenhypothese) ist also aus unendlich vielen Werten $p$ zusammengesetzt.

Wir halten noch die Entscheidungsregel fest:

• $X \le 25 \Rightarrow H_0$ wird angenommen
• $X \gt 25 \Rightarrow H_0$ wird verworfen

Fehler 1. Art berechnen

Nun können wir die Wahrscheinlichkeit für den Fehler 1. Art berechnen: $P ($Fehler 1. Art$)$. $H_0$ ist also richtig, wird aber für $H_1$ verworfen. Dafür können wir auch schreiben: $P_{H_0}($Entscheidung für $H_1)$

$\begin{array}{rcl} & = & P(X \gt 25), n = 50, p = 0,4\\ & = &1 - P(X \le 25)\\ & = & 1 - F(50; 0,4; 25)\\ & \approx & 1 - 0,9022\\ & = & 0,0978\\ & = & 9,78 ~\%\\ \end{array}$

Wir sprechen nun von einem Signifikanzniveau von $9,78 ~\%$. Dieser Wert ist nicht super, aber in Ordnung. Zu $9,78 ~\%$ glaubt die Pharma-Herstellerin bei obiger Entscheidungsregel, ihr Medikament sei besser, obwohl es das nicht ist.

Fehler 2. Art berechnen

Sehr ähnlich lässt sich der Fehler 2. Art berechnen: $P($Fehler 2. Art$)$. $H_1$ ist die richtige Hypothese, aber es wird trotzdem $H_0$ für richtig gehalten. Dieser Fehler wird mathematisch so geschrieben: $P_{H_1}($Entscheidung für $H_0)$

$\begin{array}{rcl} & = & P(X \lt 25), n = 50, p \gt 0,4\\ & = & F(50; p ; 25)\\ & \approx & \begin{cases} 0,5561=55,61~\% & \text{falls } p=0,5 \\ 0,0978 = 9,78~\% & \text{falls } p=0,6 \\ 0,0024 = 0,24~\% & \text{falls } p = 0,7 \end{cases} \end{array}$

Wie wir sehen, ist die Irrtumswahrscheinlichkeit umso kleiner, je größer $p$ ist. Je wirksamer das Medikament, desto geringer die Wahrscheinlichkeit, dass wir es zu Unrecht für weniger wirksam als das alte Medikament halten.

Signifikanzniveau

Zuoberst sind wir von der Entscheidungsregel ausgegangen und haben das Signifikanzniveau (Fehler 1. Art) berechnet. Normalerweise läuft das aber genau umgekehrt. Es ist ein Signifikanzniveau gegeben und daran muss sich die Entscheidungsregel orientieren: Wir legen also zuerst fest, wie wahrscheinlich ein Fehler 1. Art sein soll, und berechnen dann eine entsprechende Entscheidungsregel. Ein sinnvolles Signifikanzniveau ist in der Regel niedrig: $5~\%$ oder $1~\%$.

Zweiseitiger Signifikanztest - Beispiel

Sancho möchte die Gewichtsverteilung von Euro-Münzen untersuchen. Dahinter verbirgt sich ein zweiseitiger Signifikanztest

Er fragt sich, ob die 2-Euro-Münze fair ist: Dann müsste sie bei vielen Münzwürfen etwa gleich häufig „Kopf“ und „Zahl“ anzeigen. Er will $n=100$ Mal werfen. Er formuliert die Nullhypothese $H_0$: Die Münze ist fair: $p=0,5$ und die Gegenhypothese $H_1$: Die Münze ist nicht fair: $p \neq 0,5$.

Er legt sich vorher fest: Weicht die Anzahl an „Kopf“-Würfen um $8$ oder mehr vom Erwartungswert $50$ ab, so nehme ich an, dass die Münze nicht fair ist.

$\begin{array}{rcl} \alpha & = & P(X \le 42) + P(X \ge 58), p = 0,5\\ & = & F(100; 0,5; 42) + 1 - F(100; 0,5; 57)\\ & \approx & 0,0666 + 0,0666\\ & = & 0,1332 \end{array}$

Unter der obigen Entscheidungsregel liegt die Wahrscheinlichkeit, dass Sancho die Münze irrtümlich für unfair hält, bei $13,32~\%$. Das ist ein vergleichsweise hohes Signifikanzniveau. Vielleicht sollte Sancho seine Entscheidungsregel überdenken.

Signifikanzniveau - Beispiel

Sancho ist das Signifikanzniveau zu hoch. Er legt fest, dass er nur zu höchstens $5~\%$ einen Fehler 1. Art begehen möchte.

Weil die Intervalle links und rechts des Erwartungswertes gleich groß und symmetrisch sind, muss auch das Signifikanzniveau gleich verteilt sein:

$ \alpha \le 0,025 + 0,025 = 0,05$

Für das „linke“ Intervall muss also gelten:

$F(100; 0,5; X) \le 0,025$

Wenn Sancho einen Blick in die Tabelle für kumulierte Binomialverteilung wirft, kann er $X=39$ als kritische Grenze ablesen:

$F(100; 0,5; 39) \approx 0,0176$

Der Wert bei $X=40$ wäre schon größer als $0,025$ gewesen. Weil die Intervalle gleich groß sind, muss seine Entscheidungsregel lauten: Wenn das Ergebnis um mindestens $11$ vom Erwartungswert abweicht ($0 \le X \le 39$ und $61 \le X \le 100$), dann halte ich die Münze für unfair.