Maßstab

Inhaltsverzeichnis zum Thema

• Was ist ein Maßstab?
• Verkleinerung und Vergrößerung
• Verwenden von Maßstäben

Was ist ein Maßstab?

Der Maßstab ist ein Längenverhältnis. Es wird das Verhältnis von der Länge einer Strecke einer Abbildung, zum Beispiel einer Karte, zu der Länge der Strecke in der Wirklichkeit angegeben.

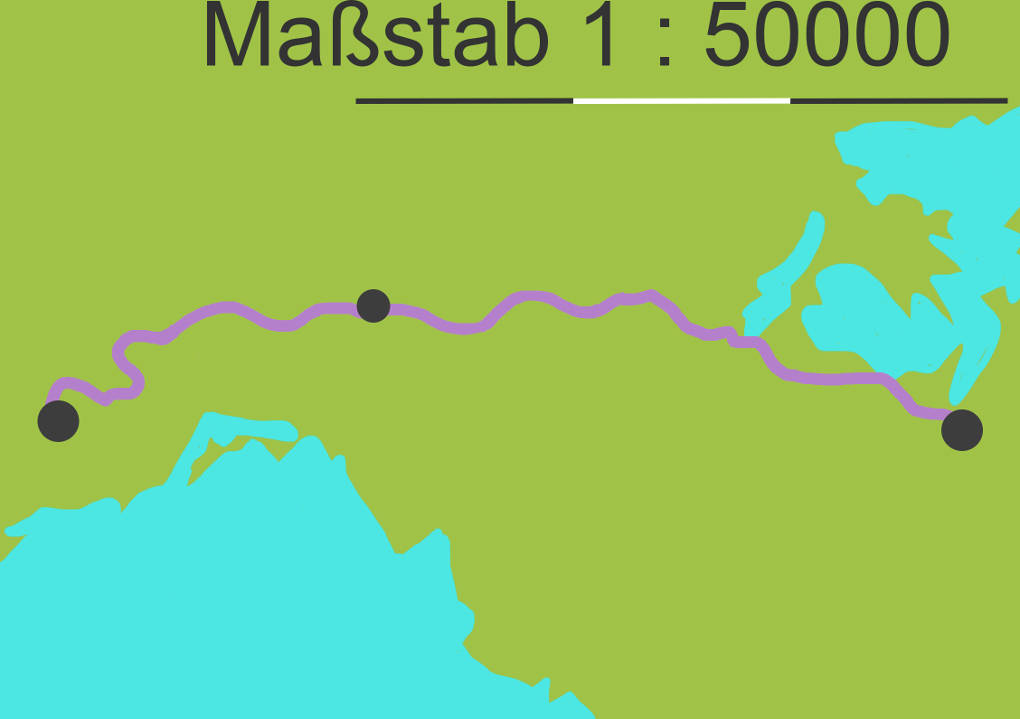
Stell dir vor: Du planst eine Fahrradtour und möchtest die Entfernung von dem linken Punkt zu dem rechten Punkt wissen. Daher misst du die Länge der Strecke auf der Karte. Der Maßstab 1 : 50000 ist oben rechts auf einer Maßstableiste angegeben. Das bedeutet, dass 1 cm auf der Karte 50000 cm in der Wirklichkeit entspricht. Wenn die gemessene Strecke auf der Karte zum Beispiel 22 cm lang ist, musst du diese Länge mit 50000 multiplizieren, um die Länge der Strecke in der Wirklichkeit zu erhalten. Diese beträgt 22 cm $\cdot$ 50000 = 1100000 cm. Dies entspricht 11 km, der Länge der Strecke ist in der Wirklichkeit.

Weitere Beispiele für Maßstäbe sind:

• 1 : 25000 bedeutet:, 1 cm auf der Karte entspricht 25000 cm in der Wirklichkeit. Du liest „1 zu 25000“
• 1 : 100000 bedeutet, dass 1 cm auf der Karte 100000 cm $\hat=$ 1 km in der Wirklichkeit entspricht.

Verkleinerung und Vergrößerung

Ein Maßstab steht also für ein Längenverhältnis, in welchem Dinge aus der Wirklichkeit dargestellt werden. Dass Dinge aus der Wirklichkeit verkleinert abgebildet werden, kennst du auch von anderen Beispielen:

• Modellautos bilden Autos in einem Verhältnis 1 : n ab. Schau mal unter ein Modellauto. Dort kannst du dieses Verhältnis entdecken.
• Wenn du einen Baum zeichnen möchtest, kannst du ihn nicht in der Originalgröße auf deinen Zeichenblock zeichnen. Du musst den Baum in einem gewissen Maßstab verkleinern.

Doch nicht nur Verkleinerungen werden angegeben, sondern auch Vergrößerungen von Maßstäben.

Mithilfe eines Mikroskops können sehr kleine Dinge, zum Beispiel ein Haar, betrachtet werden.

Wenn Dinge vergrößert werden, ist der Maßstab zum Beispiel 1000 : 1. Das bedeutet, dass das, was du unter dem Mikroskop siehst, in Wirklichkeit viel kleiner ist. Was in der Wirklichkeit 0,01 mm groß ist, wird unter dem Mikroskop in der Größe 0,01 mm $\cdot$ 1000 = 10 mm dargestellt. Dies entspricht 1 cm. Auch mit einer Lupe kannst du etwas vergrößern: Wenn du zum Beispiel eine sehr kleine Schrift nicht lesen kannst, verwendest du eine Lupe. Nun siehst du die Schrift größer, als sie in Wirklichkeit ist. Ein Maßstab 1 : n , sprich „1 zu n“, steht somit für eine Verkleinerung: 1 cm im Modell oder auf der Karte entspricht n cm in der Wirklichkeit. Dabei ist n größer als 1 und oft eine natürliche Zahl. Umgekehrt steht n : 1, sprich „n zu 1“, für eine Vergrößerung: 1 cm in der Wirklichkeit wird in einem Modell oder einer Zeichnung mit n cm dargestellt.

Verwenden von Maßstäben

In den folgenden Beispielen erkennst du, wie du Maßstäbe verwenden und mit Maßstäben rechnen kannst:

• Verkleinerung: Lisa und Tim fliegen von Köln nach Berlin. Auf einer Karte mit dem Maßstab 1 : 1000000 misst Lisa die Länge 57 cm. Wie weit ist Köln von Berlin entfernt? 57 cm $\cdot$ 1000000 = 57000000 cm. Das entspricht 570 km, der gesuchten Entfernung von Köln nach Berlin.
• Vergrößerung: Paul möchte das Kleingedruckte auf einer Schokoladentafel lesen. Dafür verwendet er eine Lupe, welche die Schriftgröße verdoppelt. Der Maßstab ist somit 2 : 1. Ein Buchstabe der Größe 2 mm ist nun in der Größe 2 $\cdot$ 2 mm = 4 mm dargestellt.
• Vergrößerung: Das menschliche Haar hat einen Durchmesser von ungefähr 0,12 mm. Wenn du den Querschnitt eines Haares unter dem Mikroskop im Verhältnis 1000 : 1 betrachtest, siehst du das Haar mit dem Durchmesser 1000 $\cdot$ 0,12 mm = 120 mm. Dies entspricht 12 cm.