Grundlagen zu Wurzeln

Inhaltsverzeichnis zum Thema

• Vom Quadrat zur Wurzel
• Wurzeln ziehen
• Irrationalität von $\sqrt{2}$

Vom Quadrat zur Wurzel

Um Wurzeln zu veranschaulichen, betrachten wir ein Quadrat, dessen Flächeninhalt verdoppelt werden soll.

Die Seitenlänge des ursprünglichen Quadrats beträgt $1\text{cm}$. Der Flächeninhalt entspricht dem Produkt der Seitenlängen. Es gilt also:

$A = a\cdot a = 1\text{cm}\cdot 1\text{cm} = 1\text{cm}^{2}$

Es liegt nun nahe zu denken, dass man einfach die Seitenlänge verdoppelt, um auf den doppelten Flächeninhalt zu kommen. Das klappt aber nicht, wie die Rechnung zeigt:

$A = 2\text{cm}\cdot 2\text{cm} = 4\text{cm}^{2}$

Wie man sieht, hat sich der Flächeninhalt vervierfacht! Welche Seitenlänge hat dann ein Quadrat mit doppeltem Flächeninhalt, also $A=2\text{cm}^{2}$? Wir betrachten folgende Rechnung:

$\begin{array}{lll} 2\text{cm}^2 &=& a\cdot a \\ &=& \sqrt{2}\text{cm}\cdot \sqrt{2}\text{cm} \\ &=& \sqrt{2\cdot 2}\text{cm}^2 \\ &=& \sqrt{4}\text{cm}^2 \\ &=& 2\text{cm}^2 \end{array}$

Die Seitenlänge des gesuchten Quadrats beträgt also $\sqrt{2} \text{cm}$. Genauso funktioniert das mit der Verdreifachung des Flächeninhalts, also mit $A=3\text{cm}^2$:

$\begin{array}{lll} 3\text{cm}^2 &=& a\cdot a \\ &=& \sqrt{3}\text{cm}\cdot \sqrt{3}\text{cm} \\ &=& \sqrt{3\cdot 3}\text{cm}^2 \\ &=& \sqrt{9}\text{cm}^2 \\ &=& 3\text{cm}^2 \end{array}$

Wurzeln ziehen

Wurzeln ziehen mit der Primfaktorzerlegung? Mit Hilfe der Primfaktorzerlegung lassen sich in drei Schritten Wurzeln ziehen. Wir zerlegen zuerst die Zahl unter der Wurzel wie folgt in ihre Primfaktoren:

$\sqrt{225} = \sqrt{3\cdot 3\cdot 5\cdot 5}$

Dann fassen wir zusammen, indem wir gleiche Zahlen als Potenz darstellen:

$\sqrt{3^{2}\cdot 5^{2}}$

Da sich Quadratwurzeln und Quadratzahlen, also Potenzen mit einem Exponenten von $2$, gegenseitig aufheben, erhalten wir:

$3\cdot 5 = 15$

Mit dieser Methode können wir auch die dritte Wurzel ziehen:

$\sqrt[3]{3375} = \sqrt[3]{5\cdot 5\cdot 5\cdot 3\cdot 3\cdot 3}= \sqrt[3]{5\cdot 5\cdot 5}\cdot\sqrt[3]{ 3\cdot 3\cdot 3} = 5\cdot 3 = 15$

Irrationalität von $\sqrt{2}$

Die Abbildung veranschaulicht, wie man ein Rechteck in ein flächengleiches Quadrat verwandeln kann.

• $A = 2\text{cm}\cdot 1\text{cm} = 2\text{cm}^{2}$ für das Rechteck
• $A=\sqrt{2} \text{cm}\cdot\sqrt{2} \text{cm} = 2\text{cm}^{2}$ für das Quadrat

Mit Hilfe des Zahlenstrahls erkennen wir, dass die Quadratseitenlänge nicht ganzzahlig ist. Sie beträgt $\sqrt{2} \text{cm}$.

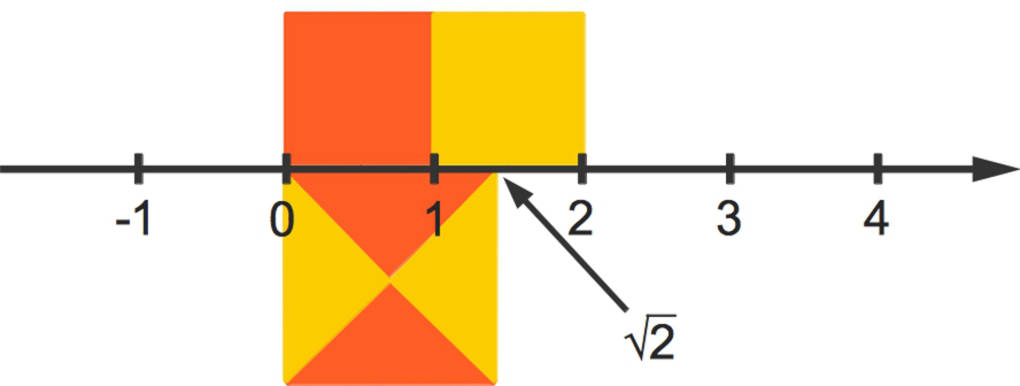
Die Wurzel aus $2$ ist eine irrationale Zahl. Das bedeutet, sie ist nicht als Bruch aus zwei ganzen Zahlen darstellbar.

Wir können die Irrationalität von $\sqrt{2}$ mit Hilfe eines Widerspruchsbeweises zeigen. Hierzu formulieren wir eine logische Gegenannahme und widerlegen diese rechnerisch. Dadurch muss die Gegenannahme falsch und somit die anfängliche Aussage richtig sein.

Aussage: $\sqrt{2}$ ist eine irrationale Zahl

$\sqrt{2} \in\mathbb{R}\setminus\mathbb{Q}$

Gegenannahme: $\sqrt{2}$ ist eine rationale Zahl

$\sqrt{2} \in\mathbb{Q}$

Beweis:

$\begin{array}{llll} \sqrt{2} &=& \frac{p}{q} & |\text{quadrieren} \\ 2 &=& \frac{p^{2}}{q^{2}} & |\cdot q^{2} \\ 2q^{2} &=& p^{2} \end{array}$

Also haben wir eine Beziehung, die besagt, dass $p^{2}$ gerade sein muss. Ist $p^{2}$ gerade, dann ist auch $p$ gerade, also gilt:

$p = 2r,\quad r\in\mathbb{N}$

In die obige Gleichung eingesetzt folgt:

$\begin{array}{llll} 4r^{2} &=& 2q^{2} &\vert :2 \\ 2r^{2} &=& q^{2} \end{array}$

Also ist auch $q$ eine gerade Zahl:

$q = 2s, \quad r\in\mathbb{N}$

Sind $p$ und $q$ jeweils gerade Zahlen, so handelt es sich bei $\frac{p}{q}$ um einen nicht vollständig gekürzten Bruch. Somit ist die Annahme einer rationalen Zahl widerlegt.