Quadratwurzeln natürlicher Zahlen

Inhaltsverzeichnis zum Thema

• Was bedeutet Quadrieren
• Was bedeutet Wurzelziehen
• Quadratzahlen
• Die Wurzel aus Quadratzahlen
• Die Wurzel anschaulich
• Wurzelgesetze
• Die Wurzel aus drei- und vierstelligen Zahlen
• Die Wurzel ziehen mit Primfaktorzerlegung
• Die näherungsweise Berechnung der Quadratwurzel
• Die Intervallschachtelung
• Das Heron-Verfahren

Was bedeutet Quadrieren

Weißt du noch, was Potenzen sind? Potenzen haben die Form

$a^{n}=\underbrace{a\cdot ...\cdot a}_{n-\text{mal}}$

Du siehst, eine Potenz ist ein Produkt, in welchem der gleiche Faktor (hier $a$) mehrmals (hier $n$-mal) vorkommt.

Beim Quadrieren ist $n=2$, also $a^{2}=a\cdot a$.

Beispiele

• $4^{2}=4\cdot 4=16$
• $11^{2}=11\cdot 11=121$
• $1,5^{2}=1,5\cdot 1,5=2,25$

Was bedeutet Wurzelziehen

Willst du nun umgekehrt wissen, welche Zahl zum Quadrat $16$ oder $121$ oder $2,25$ ist, musst du die Wurzel ziehen. Wenn man in der Mathematik von der Wurzel spricht, meint man die Quadratwurzel. Es gibt auch andere Wurzeln. Die wirst du sicher noch kennenlernen.

Du kannst eine Wurzel so definieren: Die Wurzel einer nichtnegativen Zahl $x$ ist die nichtnegative Zahl, deren Quadrat $x$ ist.

Bei den obigen Beispielen bedeutet dies:

• $4^{2}=4\cdot 4=16$, also ist $\sqrt{16}=4$.
• $11^{2}=11\cdot 11=121$, also ist $\sqrt{121}=11$.
• $1,5^{2}=1,5\cdot 1,5=2,25$, also ist $\sqrt{2,25}=1,5$.

Quadratzahlen

Quadratzahlen sind natürliche Zahlen, die das Quadrat einer anderen natürlichen Zahl sind. Umgekehrt kannst du auch die Wurzel bestimmen. Schaue dir hierfür einige Beispiel an.

Die Wurzel aus Quadratzahlen

Kennst du die Zahl, welche quadriert die Quadratzahl ergibt, so kennst du umgekehrt auch die Wurzel der Quadratzahl:

• $5^{2}=25$, also ist $\sqrt{25}=5$.
• $7^{2}=49$, somit ist $\sqrt{49}=7$.
• $12^{2}=141$ und damit weißt du, dass $\sqrt{144}=12$ ist.

Nur, wie kannst du vorgehen, wenn du die Wurzel aus einer Zahl ziehen musst, von welcher du nicht weißt, ob sie eine Quadratzahl ist?

Die Wurzel anschaulich

Der Flächeninhalt $A$ eines Quadrates mit der Seitenlänge $a$ ist $A=a^{2}$. Kennst du nun den Flächeninhalt $A$ und möchtest die Seitenlänge berechnen, kannst du $a=\sqrt{A}$ rechnen.

Du kannst auch mit dem Satz des Pythagoras die Wurzel veranschaulichen:

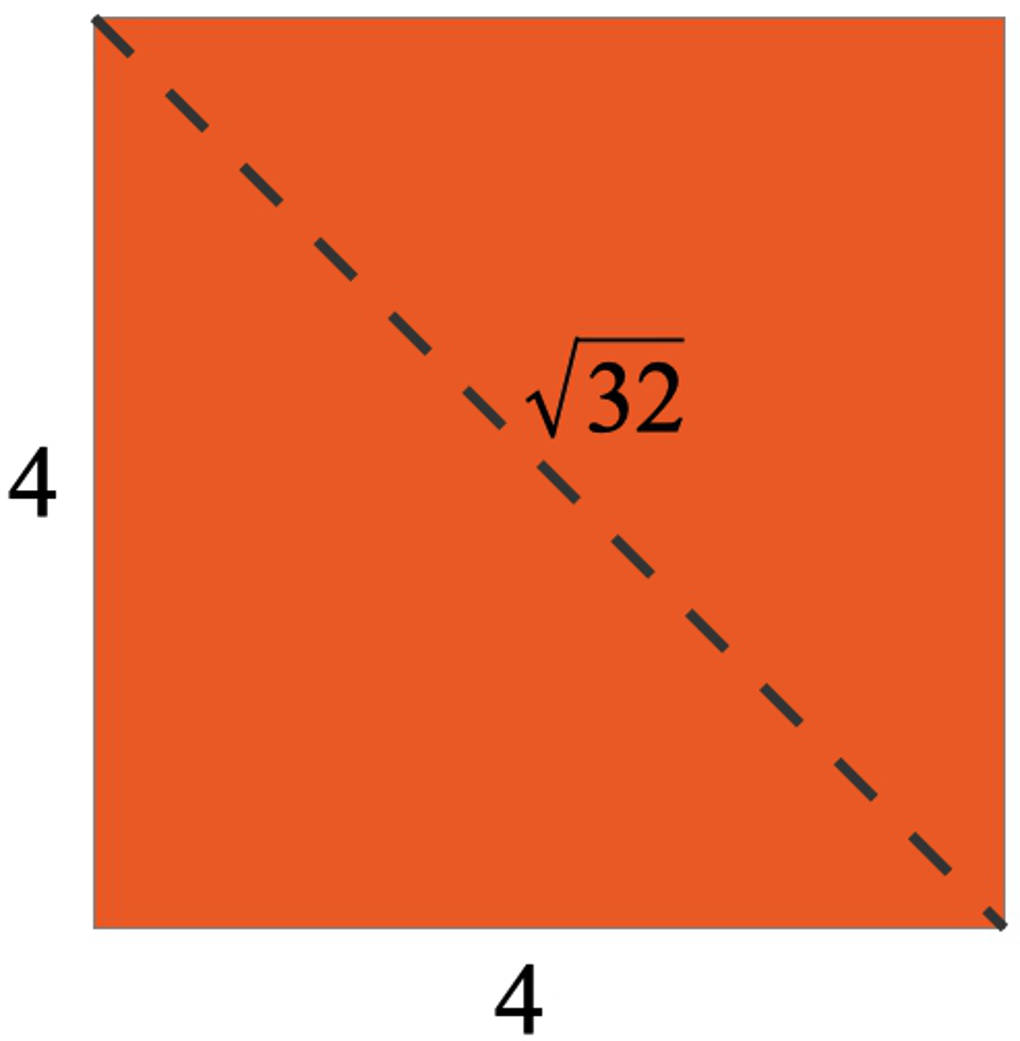
Wenn du das Quadrat entlang der gestrichelten Linie zerschneidest, erhältst du zwei kongruente rechtwinklige und gleichschenklige Dreiecke. Die gestrichelte Linie, also die Diagonale des Quadrates, ist die Hypotenuse in diesen Dreiecken und es gilt für deren Länge $d^{2}=4^{2}+4^{2}=16+16=32$, also $d=\sqrt{32}$.

Wurzelgesetze

Nun schauen wir uns an, wie du die Wurzel aus größeren Zahlen ziehen kannst.

Die Wurzel aus drei- und vierstelligen Zahlen

Wir schauen uns hierfür die Wurzel aus $2209$ an. Bekannt ist, dass $2209$ eine Quadratzahl ist.

Da zum einen $9^{2}=81$ und $10^{2}=100$ ist sowie $99^{2}=9801$ und $100^{2}=10000$ ist, kannst du schließen, dass die Wurzel aus einer drei- oder vierstelligen Zahl eine zweistellige Zahl sein muss.

• Beginne mit den Zehnern: $40^{2}=1600$ und $50^{2}=2500$. Die Zehnerzahl ist also $4$.
• Komm nun zu den Einern: Schau dir hierfür die letzte Stelle der Quadratzahl, also die $9$, an. Welche Zahlen ergeben quadriert eine Zahl mit einer $9$ an der letzten Stelle? Diese sind die $3$, da $3^{2}=9$, und die $7$, da $7^{2}=49$.
• Weil $2209$ näher an $2500$ liegt als an $1600$, muss die größere der beiden Zahlen, also die $7$, die Einerzahl sein.

Damit kannst du folgern, dass $\sqrt{2209}=47$ ist. Mach doch einmal die Probe.

Die Wurzel ziehen mit Primfaktorzerlegung

Du kannst auch die Wurzel einer Quadratzahl ziehen, wenn du deren Primfaktorzerlegung bildest. Hierfür betrachten wir die Wurzel aus $576$.

Los geht's:

• $576=2\cdot 288$
• $288=2\cdot 144$, also ist $576=2\cdot 2\cdot 144$.
• $144=2\cdot 72$, also erhältst du $576=2\cdot 2\cdot 2\cdot 72$.
• Wenn du so weiter machst, kommst du zu $576=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3$.
• Nun kannst du jeweils zwei gemeinsame Faktoren als Quadrat schreiben $576=2^{2}\cdot 2^{2}\cdot 2^{2}\cdot 3^{2}$.

Wende die Wurzelgesetze an. So erhältst du

$\sqrt{576}=\sqrt{2^{2}\cdot 2^{2}\cdot 2^{2}\cdot 3^{2}}=\sqrt{2^{2}}\cdot\sqrt{2^{2}}\cdot\sqrt{2^{2}}\cdot\sqrt{3^{2}}=2\cdot 2\cdot 2\cdot 3=24$

Die näherungsweise Berechnung der Quadratwurzel

Nun lernst du noch zwei Möglichkeiten kennen, eine Quadratwurzel näherungsweise zu bestimmen:

• die Intervallschachtelung sowie
• das Heron-Verfahren.

Die Intervallschachtelung

Diese schauen wir uns an dem Beispiel $\sqrt{5}$ an:

• Da $2^{2}=4\lt 5\lt 9=3^{2}$ ist, muss gelten $2\lt \sqrt 5\lt 3$. Nun liegt $5$ näher bei $4$ als bei $9$, also liegt auch $\sqrt{5}$ näher bei $2$ als bei $3$.
• Weiter geht's: $2,5^{2}=6,25$. Es muss also gelten $2\lt \sqrt{5}\lt 2,5$.
• $2,2^{2}=4,84$, nun weißt du bereits $2,2\lt \sqrt{5}\lt 2,5$.
• $2,3^{2}=5,29$, das bedeutet $2,2\lt \sqrt{5}\lt 2,3$. Die erste Dezimalstelle von $\sqrt{5}$ ist gefunden: $\sqrt{5}=2,2...$.
• So kannst du weiter fortfahren, je nachdem wie genau das Ergebnis sein soll: $\sqrt{5}=2,2360...$.

Übrigens: $\sqrt{5}$ ist eine irrationale Zahl.

Das Heron-Verfahren

Mit Hilfe des Heron-Verfahrens kannst du Schritt für Schritt (iterativ) die Wurzel einer Zahl bestimmen. Auch hierfür schauen wir uns das Beispiel $\sqrt{5}$ an.

Die Iterationsvorschrift für das Heron-Verfahren zur Bestimmung der Quadratwurzel von $a\ge 0$ lautet:

$x_{n+1}=\frac12\left(x_{n}+\frac{a}{x_{n}}\right)$

Dabei startest du mit einem Startwert $x_{0}$. Diesen wählst du geschickterweise so, dass er recht nahe bei der gesuchten Wurzel liegt. Probiere dies einmal mit $x_{0}=2$ zur Berechnung von $\sqrt{5}$.

1. $x_{1}=\frac12\left(2+\frac{5}{2}\right)=2,25$: Quadriere nun $2,5^{2}=5,0625$. Das ist schon recht nahe bei $5$. Rechne doch einmal weiter:
2. $x_{2}=\frac12\left(2,25+\frac{5}{2,25}\right)\approx 2,2361$. Quadriere auch hier $2,2361^{2}=5,0001...$. Du siehst, du hast schon einen recht guten Näherungswert für $\sqrt{5}$ gefunden.