Strömungen – Bewegung in dynamischen Gasen und Flüssigkeiten

Inhaltsverzeichnis zum Thema

• Einleitung
• Fluidstatik
• Dichte von Flüssigkeiten und Gasen
• Hydrostatischer Druck und Paradoxon
• Fluiddynamik
• Die Bernoulli-Gleichung
• Dynamischer Auftrieb

Einleitung

Du hast bereits die drei Aggregatzustände fest, flüssig und gasförmig kennengelernt. In der Physik werden Flüssigkeiten und Gase aber häufig unter dem Namen Fluid zusammengefasst, da sie grundsätzlich andere Eigenschaften als Festkörper aufweisen: Fluide, also homogene Flüssigkeiten und Gase, sind unter mechanischer Krafteinwirkung leicht verformbar und gelten als formlos, wohingegen Festkörper ihre Form starr beibehalten. Flüssigkeiten wie Wasser oder Benzin sowie Gase (z.B. Luft) verteilen sich immer gleichmäßig in ihrem beliebig geformten Behälter, da sie fließen können. Gleiches gilt für zähflüssige Substanzen wie Zahnpasta oder Ketchup. Wie so oft, gibt es auch hier Ausnahmen. So können auch Festkörper Fluide sein, wenn sie fließen können. Ein Beispiel wäre etwa (Treib-)Sand oder Schlamm. Aufgrund ihrer Fähigkeit zu fließen, gelten für Fluide andere physikalische Gesetzmäßigkeiten als für Festkörper. Die Strömungslehre, auch Fluidmechanik genannt, untersucht die statischen und dynamischen Eigenschaften von Fluiden.

Fluidstatik

Die Fluidmechanik ist wie die Mechanik allgemein in Statik und Dynamik unterteilt. Die Fluidstatik beschäftigt sich demnach mit den Eigenschaften von ruhenden Fluiden wie etwa Wasser in einem Gefäß. Der Zustand des Wasser ist durch seine Dichte $\rho$ gekennzeichnet. Im Allgemeinen kannst du dir merken, dass die Dichte von Gasen über Flüssigkeiten bis zu Feststoffen zunimmt. Zusätzlich hängt die Dichte vom Druck $p$ und der Temperatur $T$ ab und folgt dem folgenden Zusammenhang:

$\text{d}\rho = (\beta_T \text{d} p - \beta_p \text{d} T)$.

Dabei ist $\beta_T$ der isotherme Kompressibilitätskoeffizient und $\beta_p$ der isobare Wärmeausdehnungskoeffizient. Dies sind Materialkonstanten und unterscheiden sich für jedes Fluid.

Die Formel besagt, dass die Änderung der Dichte $\text{d}\rho$ von der Änderung des Drucks $\text{d} p $ und der Änderung der Temperatur $\text{d} T$ abhängt. Je größer der Druck in einem Gefäß, desto weniger Bewegungsspielraum haben die kleinsten Teilchen. Sie rücken daher enger zusammen und die Dichte steigt. Dies kannst du mit einer Menschenmenge vergleichen. Erhöht sich hingegen die Temperatur, so bewegen sich die Teilchen viel schneller und benötigen folglich mehr Platz. Bei steigender Temperatur sinkt also die Dichte.

Dichte von Flüssigkeiten und Gasen

Mit Hilfe obiger Formel kannst du einen Ausdruck für die Dichte von Flüssigkeiten berechnen. Für jeweils kleine isotherme Druckänderungen oder isobare Temperaturänderungen lässt sich folgender Zusammenhang herleiten:

$\rho = \dfrac{\rho_0}{\sqrt{(1+\beta_p \Delta T)(1-\beta_T \Delta p)}} $.

Dieser beschreibt den Druck einer Flüssigkeit nach Änderung der Umgebungsparameter für einen gegebenen Anfangsdruck $\rho_0$. Möchtest du stattdessen die Dichte eines Gases berechnen, so brauchst du die ideale Gasgleichung, die du schon kennen solltest. Für die Dichte von Gasen gilt der Ausdruck

$ \rho=0,0409 \cdot M$.

Dabei steht $M$ für die molare Masse des Gases. Für die Dichte von Luft, die zum Großteil aus Stickstoff und Sauerstoff besteht, kannst du unter Raumbedingungen die Dichte $1,178\,\frac{\text{kg}}{\text{m}^3}$ herleiten. Hat die Luft eine höhe Luftfeuchtigkeit, das heißt, dass sich kleine Wassertröpfchen in der Luft befinden, sinkt entgegen der intuitiven Erwartung die Dichte der Luft.

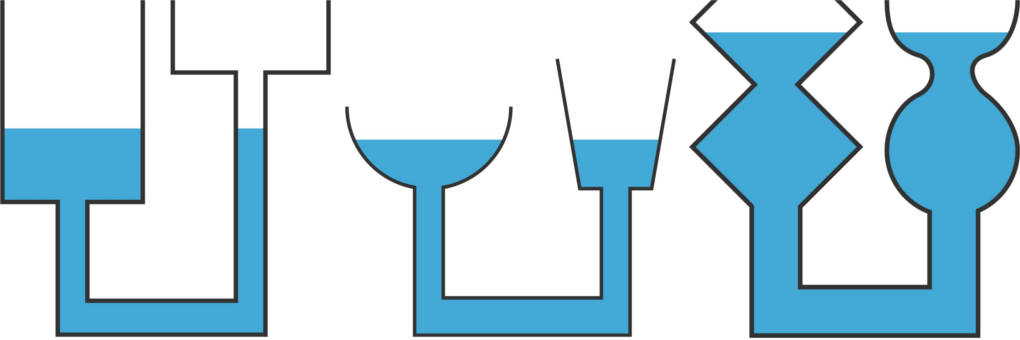
Hydrostatischer Druck und Paradoxon

Da du nun gelernt hast, wie du die Dichte von Fluiden berechnen kannst, geht es im Folgenden darum, für was du die Dichte überhaupt kennen musst. Ruht ein Fluid in einem Gefäß (Fluidstatik), so herrscht ein gewisser hydrostatischer Druck $p$ darin. Der Druck hängt dabei nur von der Dichte des Fluids und der Füllhöhe $h$ ab.

$p=\rho g h$

Das bedeutet im Umkehrschluss, dass der Druck tatsächlich unabhängig von der Menge des Fluids ist. Tauchst du im Meer einen Meter tief, wirkt auf deinen Körper derselbe Druck wie in einem Meter Tiefe im Schwimmbad, obwohl sich im Meer viel mehr Wasser befindet. Selbst in einem einen Meter langen Strohhalm herrscht derselbe Druck, obwohl dort vermutlich nur wenige Milliliter hereinpassen. Der hydrostatische Druck ist zudem unabhängig von der Form des Gefäß, was als das hydrostatische Paradoxon bekannt ist.

Fluiddynamik

Die Fluiddynamik ist der zweite Bereich der Strömungslehre und umfasst die Eigenschaften von strömenden Fluiden. Strömende Fluide sind beispielsweise Flüsse, in denen Wasser fließt. Aber auch Wind gehört als strömende Luft dazu. Fliegt ein Flugzeug durch die Luft, so gelten auch bei Windstille die Gesetze der Fluiddynamik, denn statt des durch die stille Luft fliegenden Flugzeugs könntest du dir auch ein ruhendes Flugzeug und strömende Luft vorstellen. Die Fluiddynamik erklärt viele Phänomene des Alltags, etwa warum ein Flugzeug fliegt, wieso Häuserdächer bei Sturm davon fliegen, wie Fußballer es schaffen den Fußball in einer Bananenlinie zu schießen oder auch warum dein Duschvorhang dir beim Duschen immer so nahe kommt. All diesen Phänomenen liegt der Bernoulli-Effekt zugrunde.

Die Bernoulli-Gleichung

Die Bernoulli-Gleichung folgt aus der Energieerhaltung und lautet wie folgt:

$p_0 + \rho g h + \frac{1}{2}\rho v^2 = const.$

Die Gleichung besagt, dass die Summe aus dem Umgebungsdruck $p_0$, dem hydrostatischen Druck (Höhendruck) und dem dynamischen Druck konstant ist. Der dynamische Druck wird durch den dritten Term in der Gleichung definiert und entsteht durch das Strömen des Fluids. Dabei steht $v$ für die Fließgeschwindigkeit.

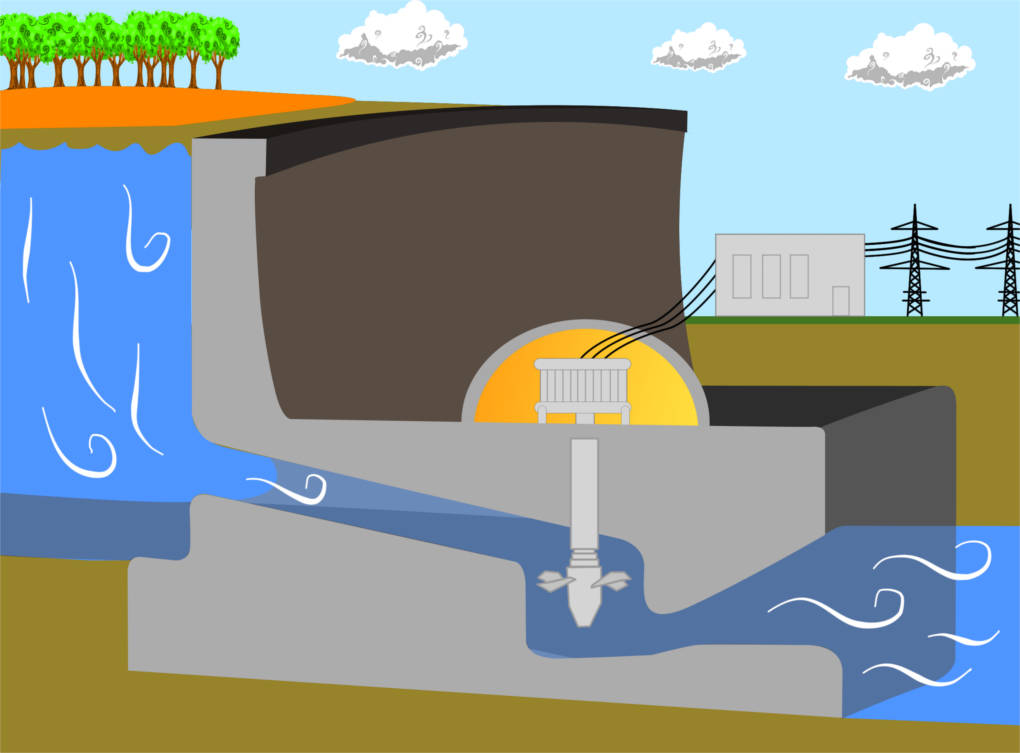
Strömendes Wasser beispielsweise verfügt über zusätzliche Bewegungsenergie. Daher ist Wasser auch heutzutage als Energieträger wertvoll, denn die Bewegungsenergie kann durch Turbinen in Staudämmen in elektrische Energie, sprich Strom, umgewandelt werden. Schon seit 2500 Jahren sind sich die Menschen der Energie des Wasser bewusst und nutzten Wasser zur Energiegewinnung zum Beispiel in Mühlen oder Hammerwerken.

Dynamischer Auftrieb

Ein strömendes Fluid hat Bewegungsenergie. Diese Energie hat es übertragen bekommen und nach der Energieerhaltung und dem obigen Bernoulli-Gesetz muss daher an anderer Stelle weniger Energie vorhanden sein, denn die Summe ist konstant. Betrachte doch einmal das Beispiel des Flugzeugs. Die Flügel sind so geformt, dass die Luft oberhalb des Flügels schneller fließt als unterhalb. Das heißt, dass der dynamische Druck oberhalb größer ist. Damit folgt aber auch, dass der hydrostatische Druck kleiner werden muss. Insbesondere ist der hydrostatische Druck oberhalb des Flügels kleiner als unterhalb, weswegen das Flugzeug eine nach oben gerichtete Auftriebskraft spürt, die es fliegen lässt. Im Unterschied zum statischen Auftrieb, den du schon kennen gelernt hast und der Schiffe schwimmen lässt, taucht der beschriebene dynamische Auftrieb nur bei Bewegung auf.

Dies kannst du dir noch an weiteren Beispielen veranschaulichen: In der Duschkabine versetzt das fließende Wasser die Luft in Bewegung. Folglich steigt der dynamische Druck und der hydrostatische Druck sinkt. Außerhalb der Duschkabine verbleibt er allerdings unverändert, weswegen der Duschvorhang zu dir gedrückt wird. Als letztes Beispiel soll der Fußball dienen. Fußballer versetzen den Ball beim Schuss in eine Rotationsbewegung. Rotiert der Ball beispielsweise linksherum, so bewegt sich die am Ball vorbeiströmende Luft auf der linken Seite schneller als auf der rechten. Folglich sinkt links der hydrostatische Druck und der Ball fliegt eine links-gekrümmte Kurve.