Kongruenz, Drehung und Verschiebung
Wie kannst du Figuren drehen und verschieben? Und wie sehen die Figuren nach dem Drehen und verschieben aus?
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Drehung von Figuren
Du möchtest eine Figur drehen. Es ist dabei egal, welche Figur du drehen möchtest, das Vorgehen ist immer gleich. Du siehst im Folgenden die Drehung eines Dreiecks und eines Kreises.
Für jede Drehung benötigst du ein Drehzentrum $Z$ sowie einen Drehwinkel $\alpha$.
Drehung eines Dreiecks
Ein Dreieck soll um das Drehzentrum $Z$ mit dem Drehwinkel $\alpha=50^\circ$ gedreht werden.
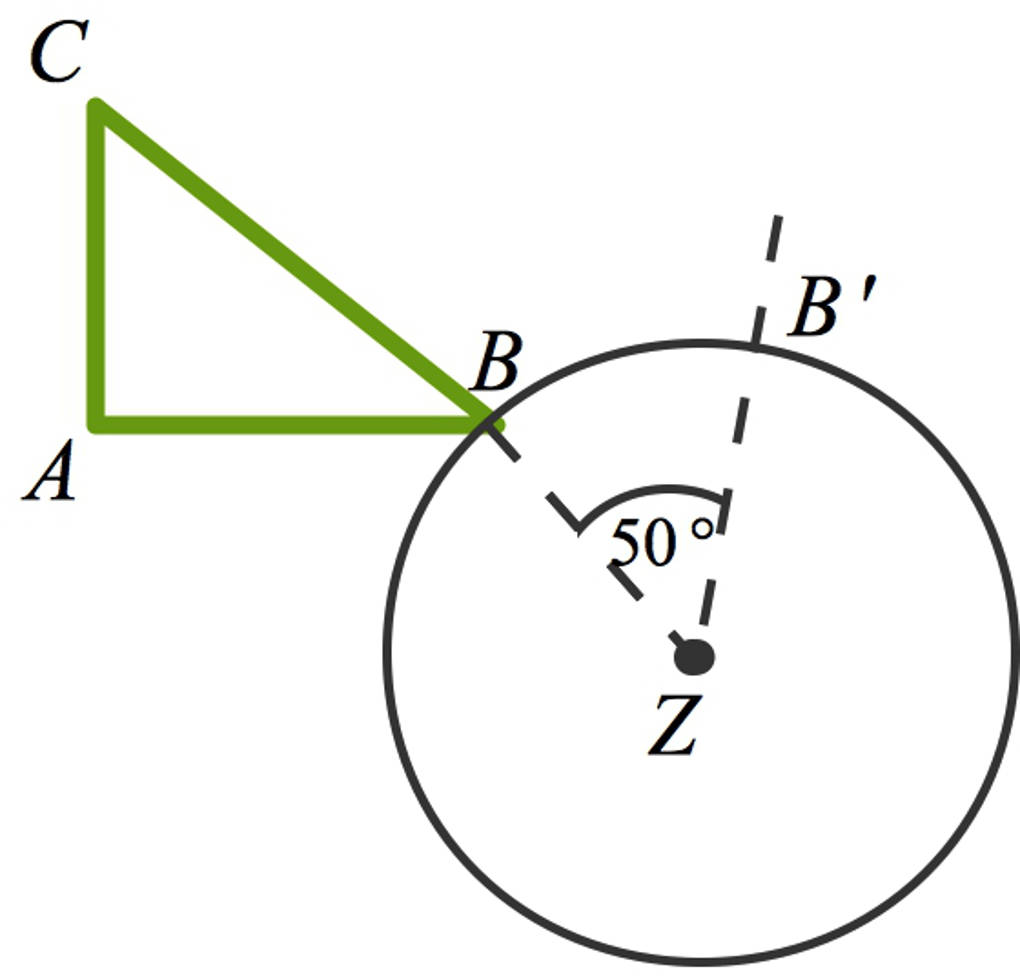
- Du verbindest einen Eckpunkt der zu drehenden Figur (hier $B$) mit $Z$.
- Dann zeichnest du einen Kreisbogen um $Z$, dessen Radius gerade dem Abstand von $B$ zu $Z$ entspricht.
- Nun trägst du den Winkel $\alpha=50^\circ$ im Punkt $Z$ an die Stecke $\overline{ZB}$ an.
- Der Schenkel schneidet den Kreisbogen. Der Schnittpunkt ist der Bildpunkt $B'$ des Punktes $B$.
Ebenso drehst du die übrigen beiden Punkte $A$ und $C$ und erhältst die Bildpunkte $A'$ sowie $C'$. Schließlich verbindest du die Eckpunkte des Dreiecks wieder miteinander. Das Dreieck $\triangle_{ABC}$ ist die Ursprungs- oder Originalfigur. Das Dreieck $\triangle_{A'B'C'}$ ist die Bildfigur, welche durch die angegebene Drehung entstanden ist.
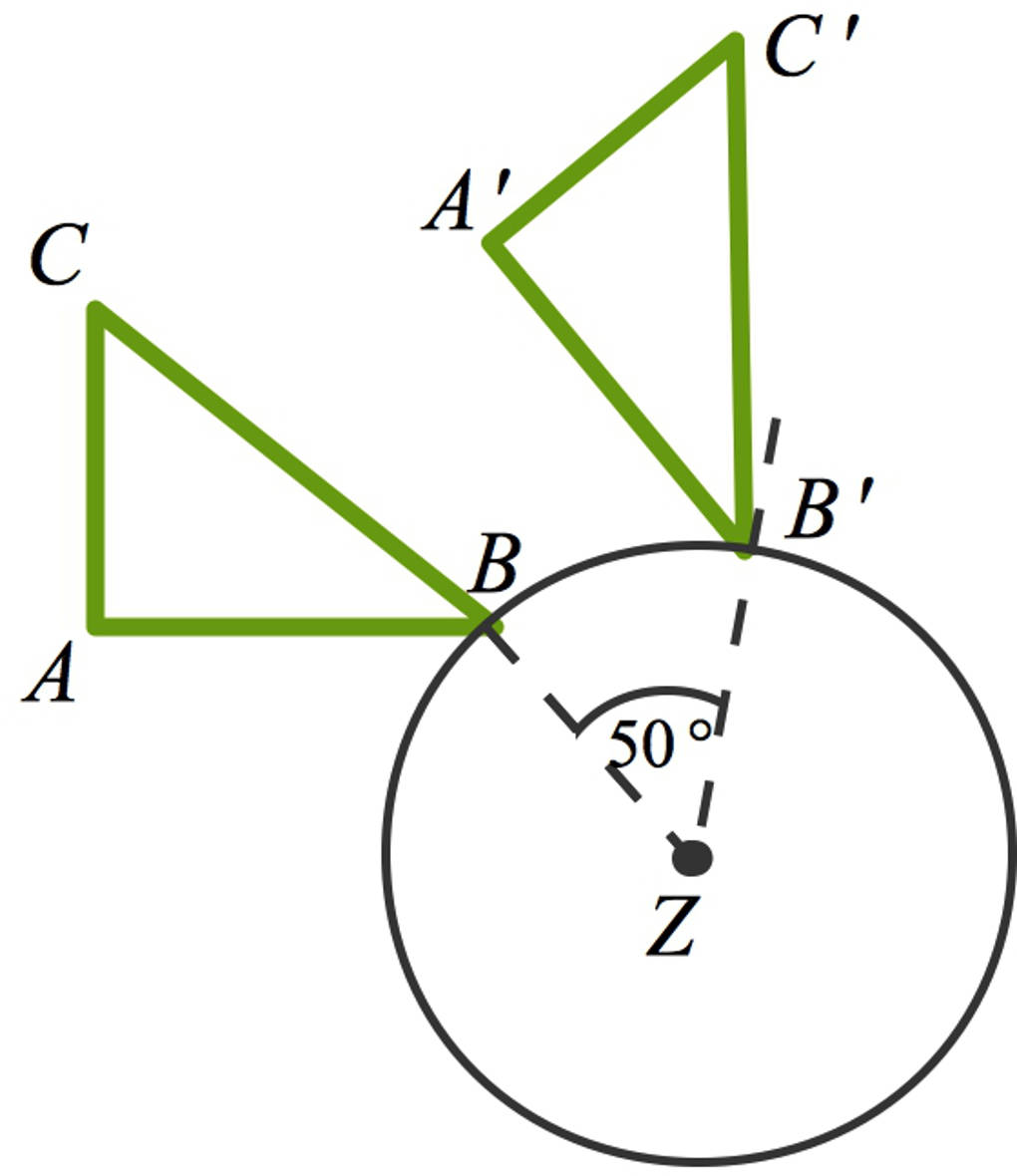
Fällt dir etwas auf?
- Das Bilddreieck sieht genauso aus wie das Ursprungsdreieck.
- Die Längen sind erhalten geblieben. Das nennt man längentreu.
- Auch die Winkel sind erhalten geblieben. Das nennt man winkeltreu.
Übrigens: Ebenso wie ein Dreieck kannst du jedes beliebige Vieleck drehen. Du drehst jeden Eckpunkt und verbindest diese wieder in der gleichen Art wie in dem Ursprungsvieleck.
Drehung eines Kreises
Bei der Drehung eines Kreises gehst du ein wenig anders vor. Hier drehst du den Mittelpunkt $M$ des Kreises um das Drehzentrum $Z$ mit dem Drehwinkel $\alpha$. Das geht ebenso wie bei dem Dreieck beschrieben. So erhältst du den Bildpunkt $M'$ des Mittelpunktes $M$. Nun zeichnest du einen Kreis um den Bildpunkt $M'$ mit dem Radius des Originalkreises und erhältst so den Bildkreis.
Drehsymmetrie
Manche Figuren besitzen ein Drehzentrum $Z$ in ihrem Inneren, um das man sie mit einem Drehwinkel $\alpha$ drehen kann, so dass sie wieder genauso aussehen wie vor der Drehung. Eine solche Figur ist dann drehsymmetrisch mit dem Drehwinkel $\alpha$. Dabei muss $0^\circ\lt\alpha\lt 360^\circ$ sein.
Kennst du vielleicht drehsymmetrische Figuren? Zum Beispiel ist ein gleichseitiges Dreieck drehsymmetrisch.
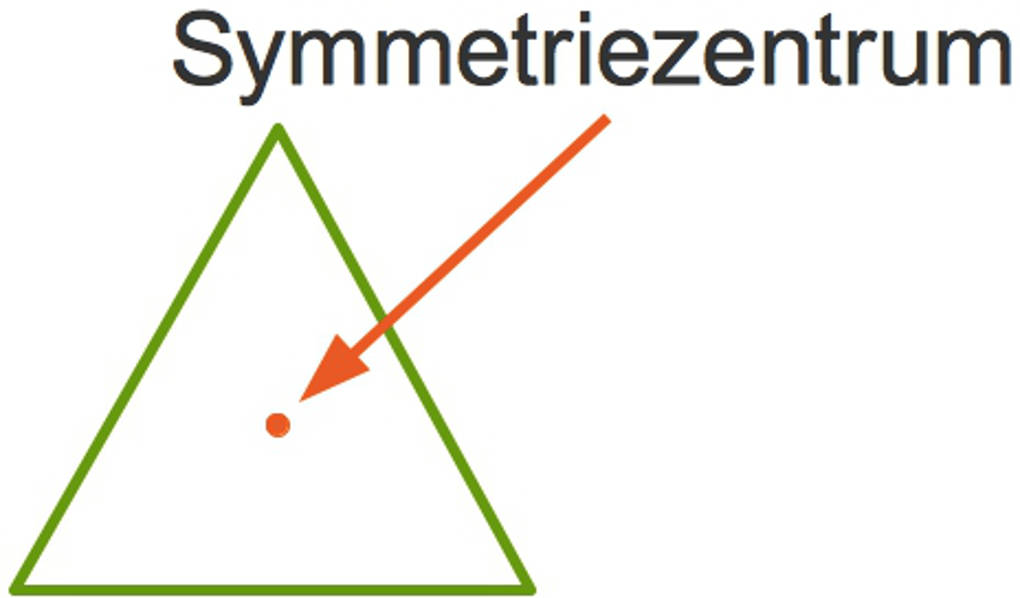
Auch ein Quadrat, ein Rechteck, eine Raute und ein Parallelogramm sind drehsymmetrisch.
Parallelverschiebung von Figuren
Du kannst Figuren auch parallel verschieben. Das schauen wir uns wieder am Beispiel eines Dreiecks an.
Du verschiebst jeden Eckpunkt des Dreiecks entlang eines Verschiebungspfeils, welcher eine gegebene Länge hat. Der Verschiebungspfeil ist in den beiden folgenden Bildern blau eingezeichnet. Du siehst hier am Beispiel des Eckpunktes $A$ die Verschiebung. Der so erhaltene Punkt $A'$ wird als Bildpunkt bezeichnet.
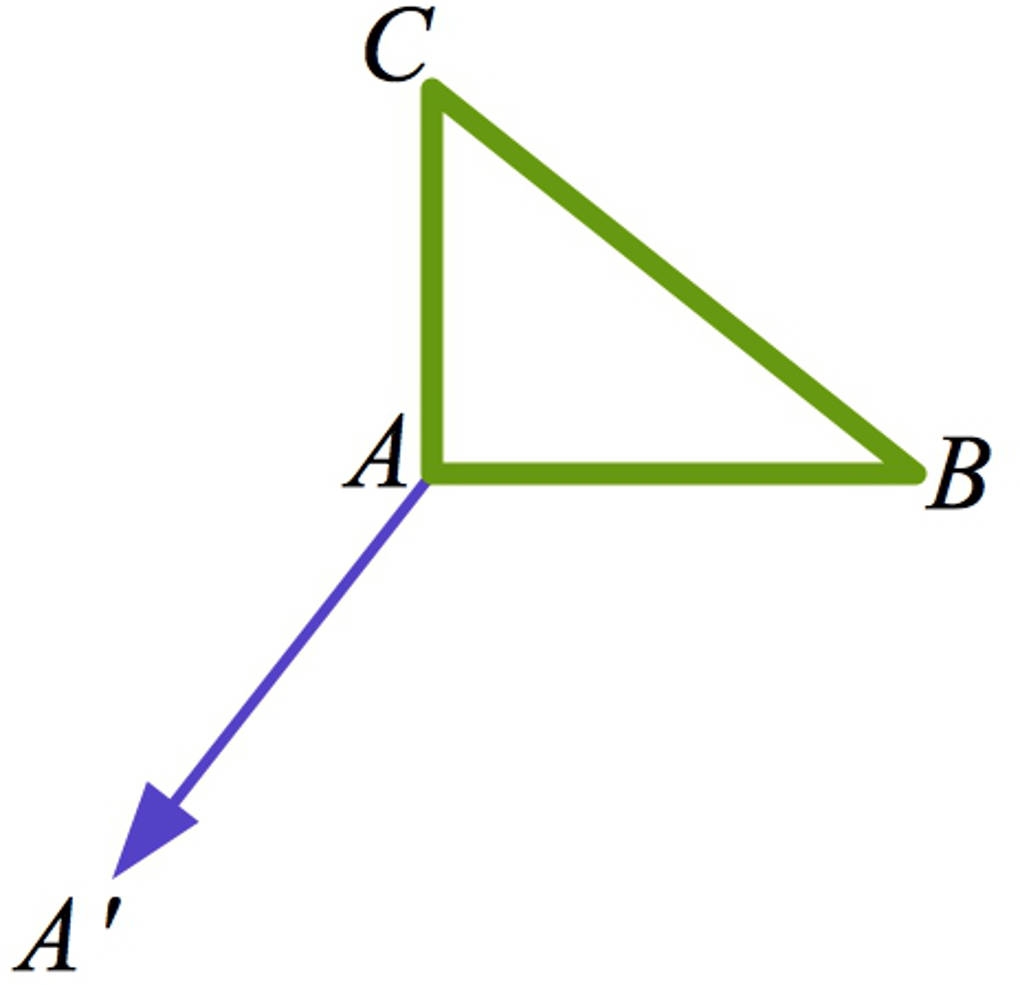
Ebenso verschiebst du die verbleibenden Eckpunkte $B$ und $C$ zu den Bildpunkten $B'$ und $C'$. Verbinde schließlich die Eckpunkte, so erhältst du das Bilddreieck $\triangle_{A'B'C'}$.
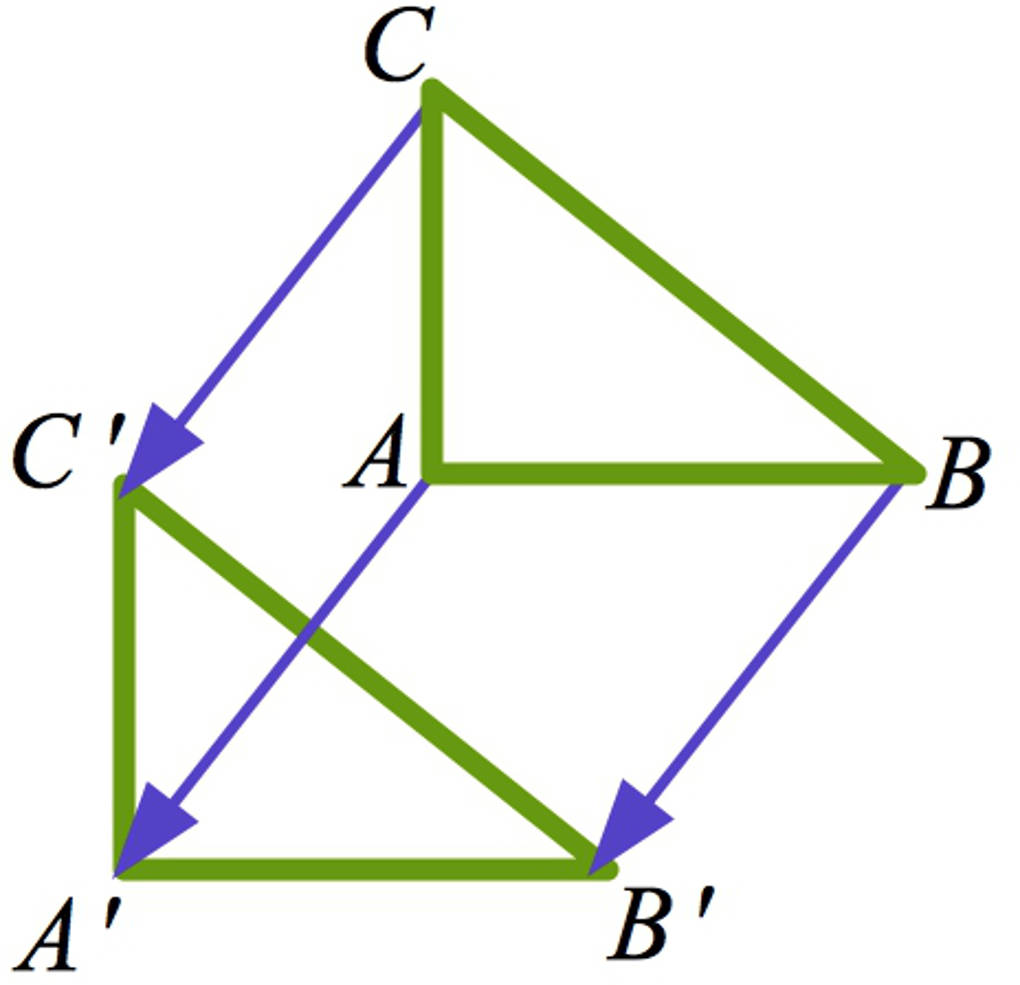
Auch hier könnte dir auffallen, dass die Dreiecke gleich sind. Das wird allerdings in der Mathematik ein wenig anders bezeichnet: Die Dreiecke sind deckungsgleich. Was bedeutet das? Wenn du die beiden Dreiecke, also das Ursprungsdreieck und auch das Bilddreieck, ausschneidest und diese übereinander legst, kannst du feststellen: Die beiden Dreiecke decken sich gegenseitig vollständig ab. Ein anderes Wort für deckungsgleich ist kongruent.
Schließlich kannst du die Drehung und Verschiebung von Figuren auch kombinieren.
Kongruenzabbildungen
Durch die beiden hier aufgeführten Abbildungen, die Drehung und die Verschiebung von Figuren, erhältst du immer Bildfiguren, die kongruent zu den Ursprungsfiguren sind. Deshalb nennt man diese Abbildungen auch Kongruenzabbildungen.
Übrigens: Auch Spiegelungen sind Kongruenzabbildungen. Es gibt Achsenspiegelungen und Punktspiegelungen. Die Punktspiegelung ist nichts anderes als eine Drehung um $180^\circ$.
Alle Videos zum Thema
Videos zum Thema
Kongruenz, Drehung und Verschiebung (6 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Kongruenz, Drehung und Verschiebung (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter










 Drehung von Figuren
Drehung von Figuren
 Drehsymmetrie
Drehsymmetrie
 Parallelverschiebung von Figuren
Parallelverschiebung von Figuren
 Parallelverschiebung
Parallelverschiebung
 Kongruenz
Kongruenz












