Flächeninhalt und Umfang von Vielecken

Inhaltsverzeichnis zum Thema

• Fünfecke
• Der Umfang eines Fünfecks
• Der Flächeninhalt eines Fünfecks
• Die Heronsformel
• Allgemeine Fünfecke
• Beispiel
• Regelmäßige Fünfecke

Fünfecke

Fünfecke haben fünf Ecken. Hier siehst du ein allgemeines Fünfeck. Die Ecken sind entgegen dem Uhrzeigersinn mit $A$ bis $E$, die Seiten mit den entsprechenden Kleinbuchstaben $a$ bis $e$ beschriftet.

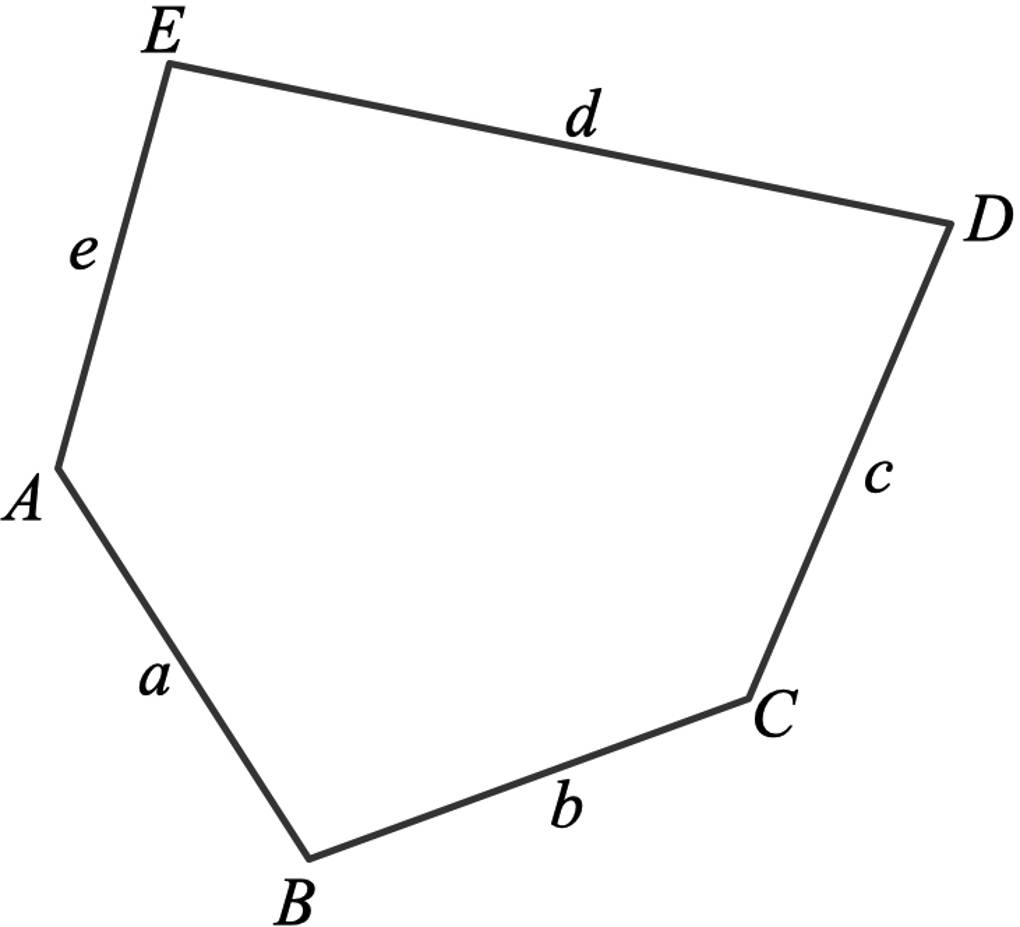
Übrigens: In jedem Fünfeck gilt, dass die Summe der fünf Innenwinkel $540^\circ$ beträgt.

Der Umfang eines Fünfecks

Der Umfang eines Fünfecks ist, wie bei jedem Vieleck, die Summe der Seitenlängen:

$u=a+b+c+d+e$

Ganz so einfach ist der Flächeninhalt nicht zu berechnen.

Der Flächeninhalt eines Fünfecks

Zunächst einmal lernst du, wie du ganz allgemein den Flächeninhalt eines Fünfecks berechnen kannst. Schließlich lernst du noch den Spezialfall eines regelmäßigen Fünfecks kennen.

Die Heronsformel

Mithilfe der Heronsformel kannst du den Flächeninhalt eines Dreiecks ausschließlich mit den Seitenlängen $a$, $b$ und $c$ berechnen.

Zunächst wird die Länge $s$ wie folgt definiert: $s=\frac{a+b+c}2$.

Damit lässt sich der Flächeninhalt eines Dreiecks wie folgt berechnen:

$A_\triangle=\sqrt{s\cdot(s-a)\cdot (s-b)\cdot (s-c)}$

Allgemeine Fünfecke

Wenn du die Punkte $A$ und $D$ sowie $B$ und $D$ miteinander verbindest, kannst du das Fünfeck in drei Dreiecke aufteilen. Der Flächeninhalt des Fünfecks ist gerade die Summe der Flächeninhalte der drei Dreiecke.

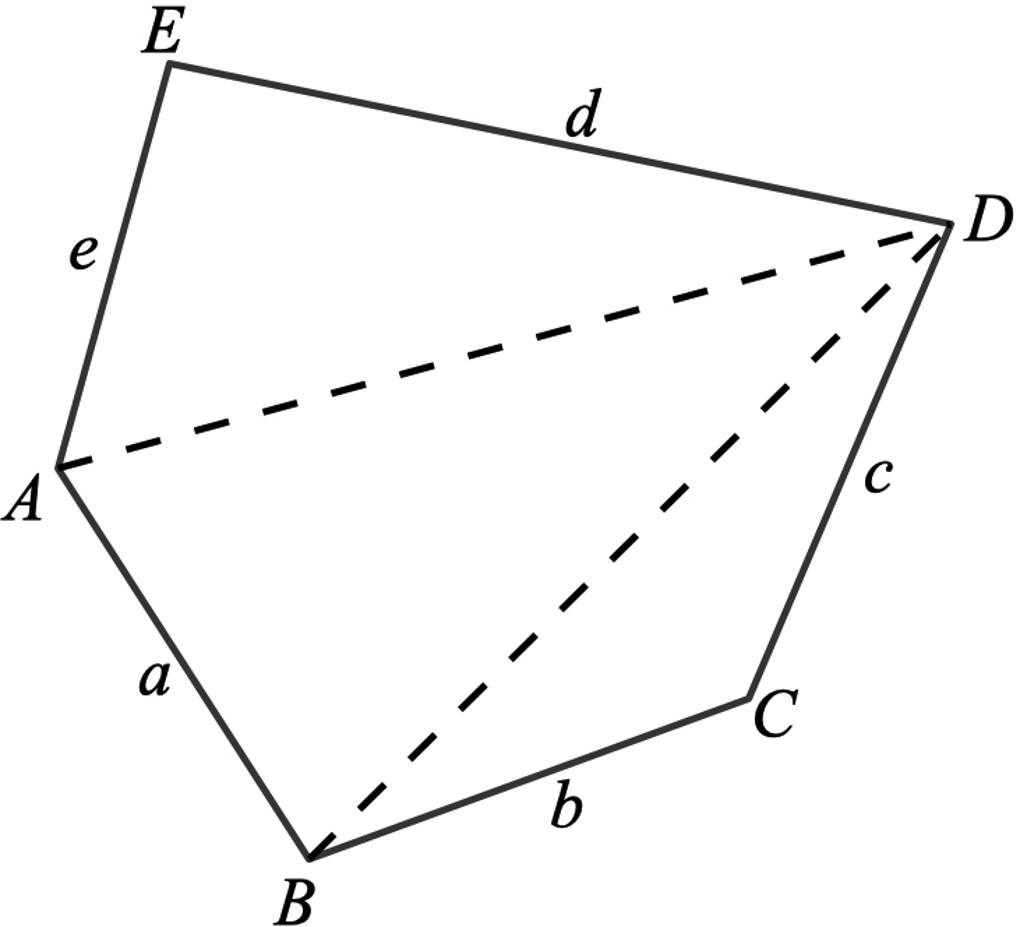
Jeden dieser Flächeninhalte kannst du mithilfe der Heronsformel berechnen.

Beispiel

Nun kannst du an dem folgenden Beispiel diese Formel üben.

Für den Abstand zweier Punkte $P(p_1|p_2)$ sowie $Q(q_1|q_2)$ kannst du die folgende Formel verwenden:

$d(P;Q)=\sqrt{(p_1-q_1)^2+(p_2-q_2)^2}$

Berechnung des Flächeninhaltes des Dreiecks $\triangle{ADE}$ mit den Punkten $A(-3|2)$, $D(4|4)$ und $E(0|5)$:

• $\overline{AE}=\sqrt{3^2+3^2}=\sqrt{18}$
• $\overline{AD}=\sqrt{7^2+2^2}=\sqrt{53}$
• $\overline{DE}=\sqrt{(-4)^2+1^2}=\sqrt{17}$

Nun kann es losgehen:

• $s=\frac{\sqrt{18}+\sqrt{53}+\sqrt{17}}2$
• $A_1=7,5$

Ebenso kannst du die Flächeninhalte der Dreiecke $\triangle{ABD}$ sowie $\triangle{BCD}$ berechnen:

• $\triangle{ABD}$: $A_2=12,5$
• $\triangle{BCD}$: $A_3=7,5$

Zuletzt addierst du diese Flächeninhalte zu $A=A_1+A_2+A_3=27,5$.

Regelmäßige Fünfecke

Bei einem regelmäßigen Fünfeck sind alle Seiten gleich lang.

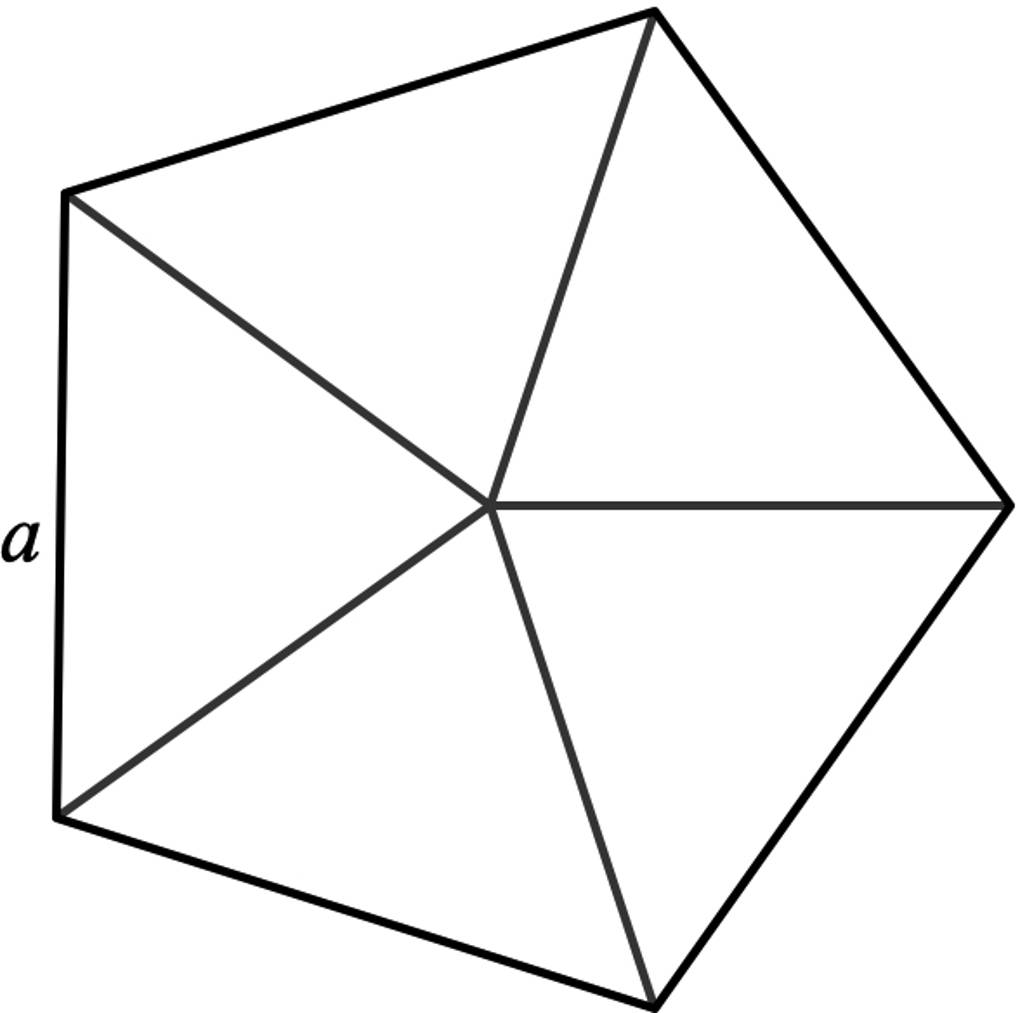
Der Umfang ist gegeben durch $u=5a$.

Wenn du jeden Eckpunkt mit dem Mittelpunkt des Fünfecks verbindest, erhältst du fünf gleichschenklige und kongruente Dreiecke. Der Flächeninhalt des Fünfecks ist somit das Fünffache eines solchen Dreiecks. Du erhältst also folgende Formel für den Flächeninhalt:

$A=\sqrt{25+10\cdot\sqrt5}\cdot\frac{a^2}4\approx1,7205\cdot a^2$