Mechanische Wellen
Die Entstehung verschiedener Arten von mechanischen Wellen, ihre Kenngrößen sowie Ausbreitungseigenschaften wie Reflexion, Brechung und Beugung
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine mechanische Schwingung?
- Von der Schwingung zur Welle
- Kenngrößen der mechanischen Wellen
- Verschieden Arten von mechanischen Wellen
Was ist eine mechanische Schwingung?
Die mechanischen Wellen werden von mechanischen Schwingern erzeugt. Daher solltest du zunächst wiederholen, was du über mechanische Schwingungen gelernt hast. Ein Gewicht $m$, das an einer Feder befestigt ist, ein sogenanntes Federpendel, ist ein schwingungsfähiges System.
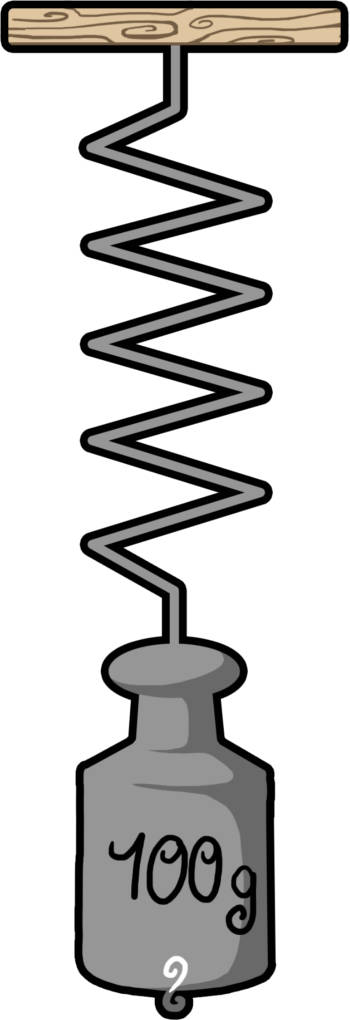
Ist das Federpendel ungestört, bleibt es zunächst bewegungslos in seiner Ruhelage. Durch eine kurze Störung, dies ist in der Regel eine Auslenkung nach oben und anschließendes Loslassen, kann das Federpendel aber zum Schwingen angeregt werden. Sich selbst überlassen führt das Federpendel nun eine harmonische Schwingung mit bestimmter Frequenz $f$ bzw. Schwingungsdauer $T$ und Amplitude $s_0$ aus. Die Amplitude entspricht der Größe der Auslenkung. Die Frequenz steht dabei für die Anzahl der Schwingungen pro Sekunde und ist der Kehrwert der Schwingungsdauer:
$f=\frac1{T} $.
Eine viertel Periode (Schwingungsdauer) nach dem Loslassen durchläuft das Gewicht seine Ruhelage. Eine weitere Viertelperiode später erreicht es seinen unteren Umkehrpunkt. Die Feder ist zu diesem Zeitpunkt maximal ausgelenkt und zieht sich anschließend wieder zusammen. Das Gewicht bewegt sich daher wieder nach oben, durchläuft erneut die Ruhelage in umgekehrter Richtung und erreicht nach einer ganzen Periode schließlich wieder den oberen Umkehrpunkt (Anfangspunkt). Trägst du die Auslenkung des Federpendels über die Zeit auf, so erhältst du eine Sinusfunktion.
Von der Schwingung zur Welle
Eine mechanische Welle ist die räumliche Ausbreitung einer mechanischen Schwingung. Dazu ist ein Medium notwendig. Mechanische Wellen wie beispielsweise Schallwellen können sich in Luft, Wasser oder auch Festkörpern ausbreiten. Dabei schwingen die Moleküle des Mediums wie ein Federpendel. Im Vakuum des Weltalls hingegen können sich keine Schallwellen ausbreiten. Im Gegensatz dazu sind elektromagnetische Wellen wie Licht nicht auf ein Medium angewiesen (das Licht der Sonne erreicht uns durch das Weltall hindurch). Bei elektromagnetischen Wellen schwingen die elektrischen und magnetischen Felder.
Entstehung mechanischer Wellen
Nachdem du das Federpendel nun verstanden hast, stelle dir vor, du hängst sehr viele gleiche Federpendel nebeneinander auf und verbindest die Gewichte mit einem Gummiband. Lenkst du nun das erste Pendel aus, so folgt das zweite aufgrund des Gummibandes kurze Zeit später. Nach einiger Zeit schwingen schließlich alle Federpendel mit gleicher Frequenz und Amplitude, allerdings zeitlich versetzt zueinander. Du hast nun eine mechanische Welle erzeugt. Sie wurde durch eine einzige mechanische Schwingung angeregt und durch das Medium Gummiband auf weitere Schwinger räumlich ausgebreitet. Dabei wird Schwingungsenergie übertragen, ohne dass Stofftransport stattfinden muss. Nach demselben Prinzip breiten sich auch Schallwellen und Wasserwellen aus.
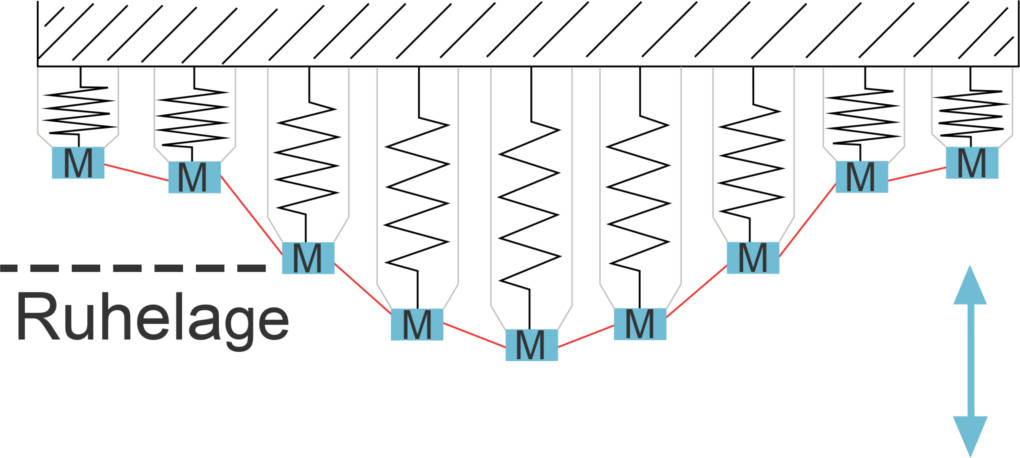
Kenngrößen der mechanischen Wellen
Bei einer mechanischen Welle folgt auf jeden Wellenberg ein Wellental. Den Abstand zweier Wellenberge (allgemein der Abstand zweier in gleicher Phase schwingender Punkte) wird als Wellenlänge $\lambda$ bezeichnet. Die Wellenberge und Wellentäler breiten sich mit einer Geschwindigkeit $v$ aus. Die Kenngrößen der Welle (Wellenlänge und Ausbreitungsgeschwindigkeit) stehen durch folgende Formel im Zusammenhang mit der Frequenz der erzeugenden Schwingung:
$v=f\lambda$.
Im obigen Beispiel schwingen viele Federpendel gleichzeitig, verbunden durch ein Gummiband. Würdest du nach einer beliebigen Zeit davon ein Standbild erzeugen und die Auslenkung eines jeden Schwingers gegen seinen Ort $x$ auftragen, so erhältst du eine Sinusfunktion.
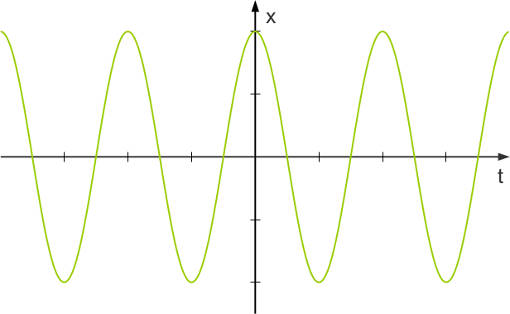
Die Auslenkung jedes einzelnen Schwingers für sich betrachtet ist gegen die Zeit $t$ aufgetragen ebenfalls eine Sinusfunktion. Eine mechanische Welle ist demnach sowohl räumlich als auch zeitlich periodisch. Dieser Zusammenhang wird durch die Wellengleichung ausgedrückt:
$s(x,t)=s_0\cdot \sin{(2\pi(\frac{t}{T}-\frac{x}{\lambda}))} $.
Die Wellengleichung vereint die Eigenschaften und Kenngrößen einer mechanischen Schwingung und einer mechanischen Welle in sich. Versuche dich doch selbst einmal an der Berechnung der Kenngrößen.
Verschieden Arten von mechanischen Wellen
Es gibt verschieden Arten von mechanischen Wellen sowie verschiedene Ausbreitungsarten. Die oben beschriebene Federpendelkette ist eine transversale Welle, da die Ausbreitungsrichtung senkrecht zur Schwingungsrichtung steht. Ein reales Beispiel für transversale Wellen sind schwingende Gitarrensaiten. Diese wiederum erzeugen Schallwellen. Schallwellen sind ebenfalls mechanische Wellen, die sich jedoch longitudinal ausbreiten. Dies bedeutet, dass die Ausbreitungsrichtung parallel zur Schwingungsrichtung ist. Bei einer Schallwelle schwingen Luftmoleküle vor und zurück und erzeugen Stellen hohen Luftdrucks (Berg) und Stellen geringen Luftdrucks (Tal). Dabei ist die Frequenz der Schwingung entscheidend für die Tonhöhe. Je größer die Frequenz (links) ist, desto höher ist der Ton. Bei kleiner Frequenz (rechts) entsteht ein tiefer Ton. Die Amplitude der Schwingung ist entscheidend für die Lautstärke des Tons.
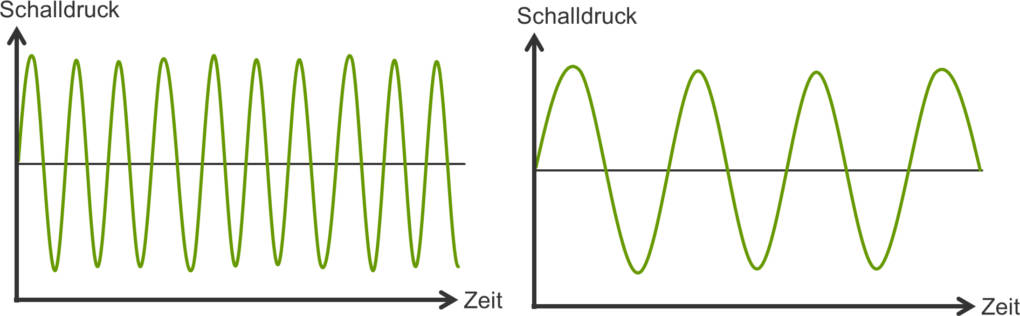
Reale Wellen breiten sich stehts räumlich in drei Dimensionen aus. Häufig überlagern sich Longitudinal- und Transversalwellen. So auch bei einem Erdbeben.
Reflexion, Beugung, Brechung
Mechanische Wellen benötigen im Gegensatz zu elektromagnetischen Wellen ein Medium, um sich auszubreiten. Gemeinsam ist beiden Wellenarten aber die Möglichkeit der Reflexion, Beugung und Brechung von Wellen. Wie Licht beispielsweise in einem Spiegel reflektiert wird, so kann auch Schall an Wänden reflektiert werden. Du kennst dieses Phänomen als Echo.

Elektromagnetische Wellen werden beim Übergang von Luft in Wasser gebrochen. Die Brechung beruht auf den unterschiedlichen Brechungsindizes der beiden Medien. Etwas Vergleichbares kann auch bei Wasserwellen passieren, wenn sie sich vom flachen ins tiefe Gewässer ausbreiten. Die Tiefe des Wassers verhält sich in etwa so wie ein Brechungsindex. Beim Übergang in tieferes Gewässer ändert sich daher die Ausbreitungsgeschwindigkeit und Wellenlänge der Wasserwellen.
Auch Beugung tritt sowohl bei elektromagnetischen wie auch mechanischen Wellen auf. Die Beugung von Licht am Doppelspalt äußert sich im Auftreten von Intensitätsmaxima und -minima auf einem Schirm. Schallwellen hingegen können beispielsweise in Türrahmen (wie ein großer Spalt) gebeugt werden und dabei ihre Richtung ändern. Nur so ist es möglich, dass du „um die Ecke“ hören kannst.
Alle Videos zum Thema
Videos zum Thema
Mechanische Wellen (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Mechanische Wellen (4 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt









 Kenngrößen mechanischer Wellen
Kenngrößen mechanischer Wellen
 Mechanische Wellen (Übungsvideo)
Mechanische Wellen (Übungsvideo)
 Mechanische Wellen – Überblick
Mechanische Wellen – Überblick
 Entstehung mechanischer Wellen
Entstehung mechanischer Wellen









