Geradengleichungen bestimmen

Inhaltsverzeichnis zum Thema

• Was ist eine lineare Funktion?
• Welche Bedingungen werden benötigt, um eine Geradengleichung aufzustellen?
• Beispiele
• Geradengleichung aus einem Punkt und der Steigung herleiten
• Geradengleichung aus zwei Punkten herleiten
• Ablesen einer Funktionsgleichung aus einem Graphen

Was ist eine lineare Funktion?

Eine lineare Funktion ist eine Funktion, deren Funktionsgleichung folgende Form hat:

$f(x)=m\cdot x+n$.

Dabei wird oft statt $f(x)$ direkt $y$ geschrieben. Inhaltlich macht das keinen Unterschied, da $f(x) = y$ gilt.

Die Variablen $m$ und $n$ werden Parameter genannt. Wir schauen uns zuerst die Bedeutung dieser Parameter an einem Beispiel an:

Gegeben sei die lineare Funktion $f$ mit der Gleichung $f(x)=0,5x-2$. Der Funktionsgraph einer linearen Funktion ist immer eine Gerade. Den Graph der Funktion $f$ siehst du hier:

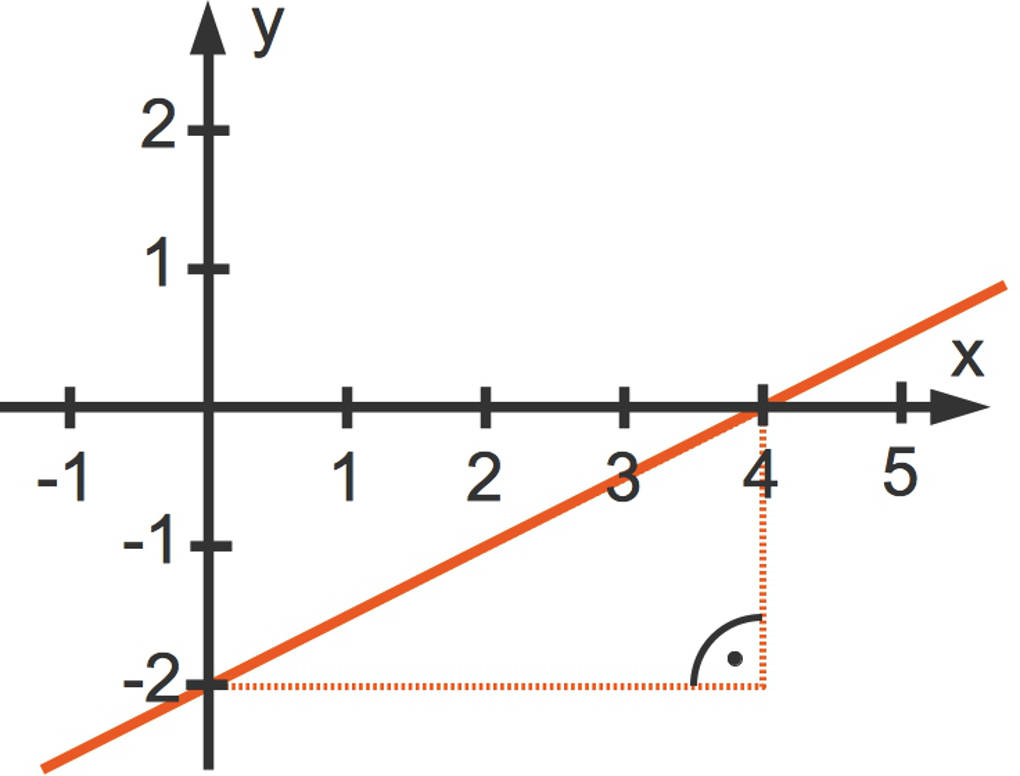
Diese Gerade schneidet die $y$-Achse bei $y=-2$. Dies entspricht dem Parameter $n$. Damit ist $n$ der sogenannte $y$-Achsenabschnitt der Geraden.

Als Ergänzung zu der Geraden siehst du in dem Bild ein rechtwinkliges Dreieck. Mit Hilfe dieses Dreiecks kann man die Steigung einer linearen Funktion bestimmen. Deshalb wird es auch Steigungsdreieck genannt. Um die Steigung zu bestimmen, wählst du zwei beliebige Punkte auf dem Graphen der Funktion aus. Wir wählen hier $P_1(4|0)$ und $P_2(0|-2)$. Mit diesen berechnest du nun die Differenzen $\Delta y$ (Differenz der $y$-Werte) und $\Delta x$ (Differenz der $x$-Werte) und bildest anschließend den Quotienten. Hier siehst du dies am Beispiel:

$\dfrac{\Delta y}{\Delta x} = \dfrac{0 - (-2)}{4 - 0} = \dfrac{2}{4} = 0,5$.

Auf diese Weise erhältst du den Parameter $m$, den Faktor vor der Variablen $x$. Dieser wird als Steigung oder Anstieg der Geraden bezeichnet.

Welche Bedingungen werden benötigt, um eine Geradengleichung aufzustellen?

Hier siehst du nun, wie du eine lineare Funktionsgleichung aus verschiedenen Informationen aufstellen kannst. Dazu unterscheiden wir drei Fälle, die teilweise aufeinander aufbauen:

• Du hast einen Punkt und die Steigung gegeben.
• Du hast zwei Punkte gegeben.
• Du hast einen Funktionsgraphen gegeben.

Beispiele

Dies schauen wir uns nun jeweils an einem Beispiel an.

Geradengleichung aus einem Punkt und der Steigung herleiten

In diesem Beispiel weißt du bereits, dass die Steigung der gesuchten Funktion $m=-2$ ist. Dadurch hat die Gleichung bereits die Form $f(x) = -2x + n$. Außerdem weißt du, dass der Punkt $Q(1|-1)$ auf dem Graphen liegt. Da jeder Punkt auf dem Graphen die Gleichung erfüllen muss, kannst du die Koordinaten des Punktes $Q$ in die Gleichung $f(x)=-2x+n$ einsetzen:

$\begin{array}{rclll} -1&=&-2\cdot 1+n&|&+2\\ 1&=&n\end{array}$.

Die Funktionsgleichung lautet also $f(x)=-2x+1$. Hier siehst du den Graphen der Funktion:

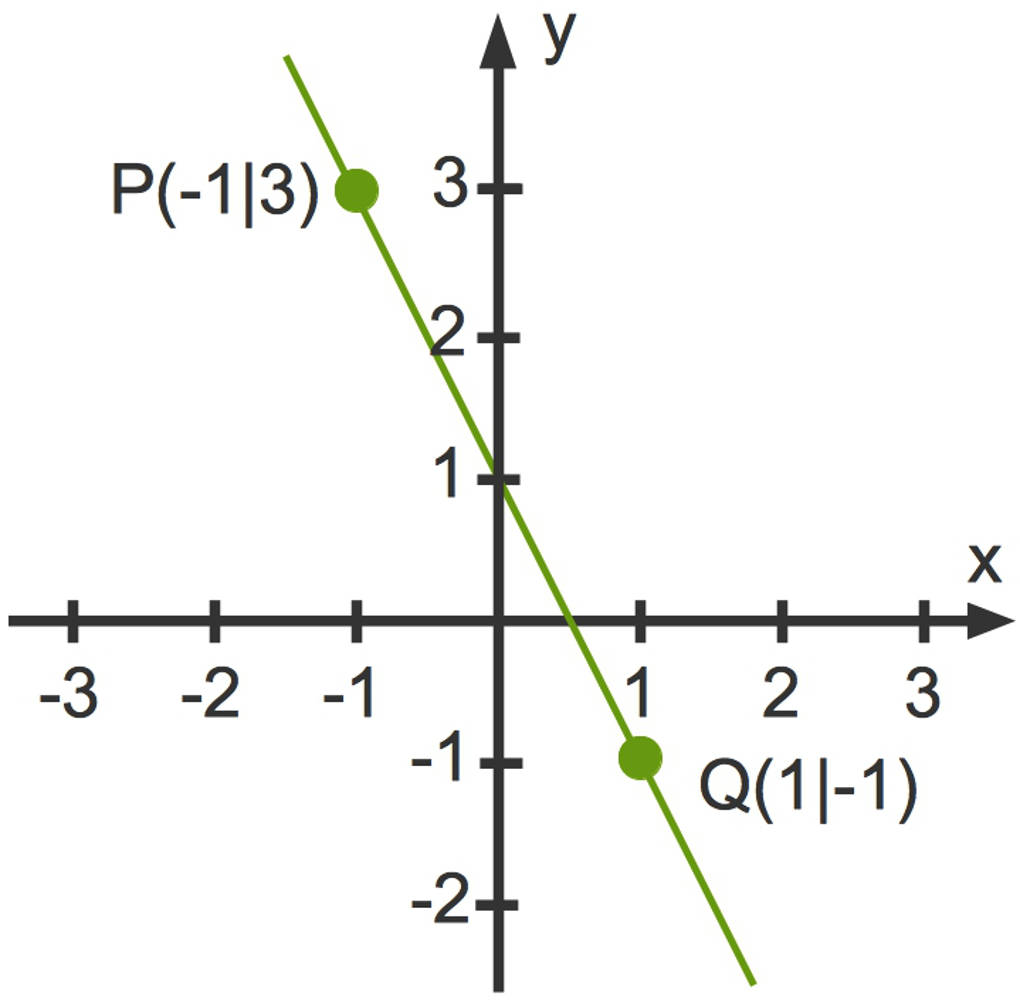
Geradengleichung aus zwei Punkten herleiten

Eine Gerade ist durch zwei Punkte eindeutig festgelegt. Wenn du also zwei Punkte in ein Koordinatensystem einzeichnest, kannst du diese durch eine eindeutige Gerade verbinden.

Für dieses Beispiel seien die Punkte $P(-1|3)$ und $Q(1|-1)$ gegeben. Diese siehst du auch schon oben in dem Koordinatensystem:

Zuerst bestimmst du die Steigung, indem du die Differenz der $y$-Koordinaten durch die der $x$-Koordinaten dividierst. Achte dabei auf die Reihenfolge. Allgemein gilt:

$m=\dfrac{q_y-p_y}{q_x-p_x}$.

Dies kannst du gleich einmal für die beiden Punkte $P(-1|3)$ sowie $Q(1|-1)$ machen.

$m=\dfrac{-1-3}{1-(-1)}=\dfrac{-4}2=-2$

Bisher lautet die Funktionsgleichung also $f(x) = -2x + n$.

Nun musst du noch den $y$-Achsenabschnitt $n$ bestimmen. Hierfür setzt du einen der beiden Punkte (egal welchen) in die Funktionsgleichung ein. Wir wählen hier $P(-1|3)$. Anschließend formst du nach $n$ um.

$\begin{array}{rclll} 3&=&-2\cdot (-1)+n&\\ 3 & = & 2 + n & | -2 \\ 1&=&n\end{array}$

So erhältst du die Funktionsgleichung $f(x)=-2x+1$. Wie du siehst, ist dies dieselbe Funktionsgleichung wie im Beispiel vorher.

Ablesen einer Funktionsgleichung aus einem Graphen

Schau dir diesen Funktionsgraphen einer linearen Funktion an.

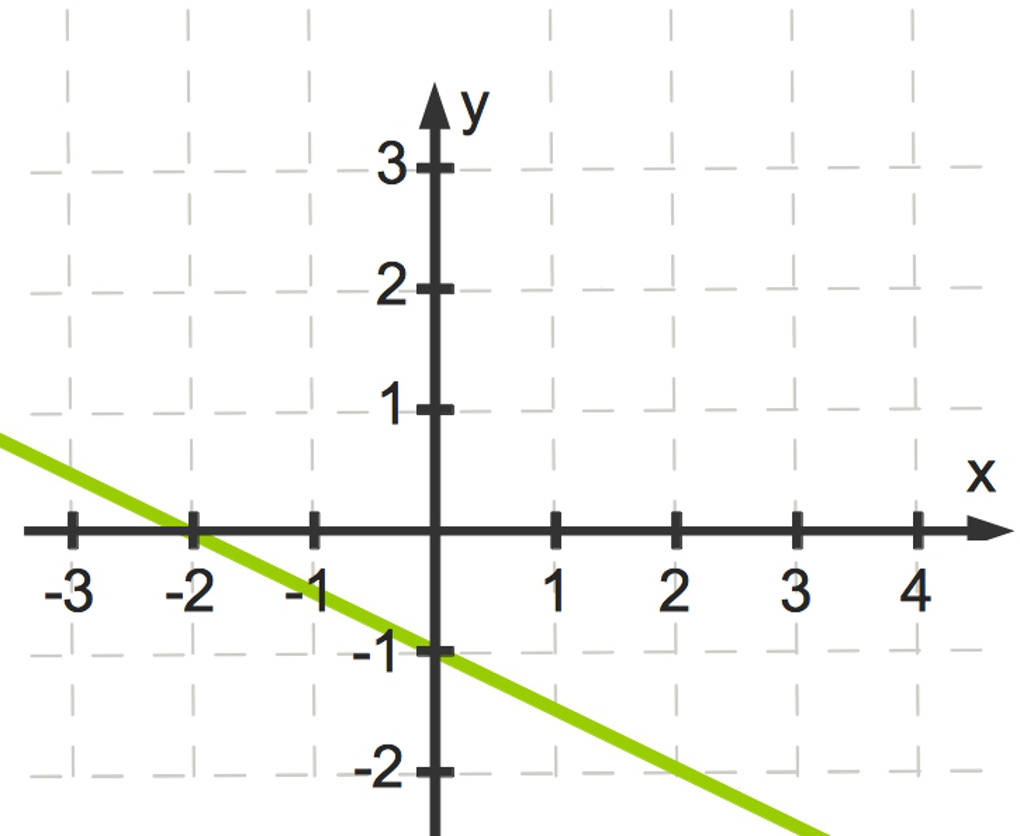
Um eine lineare Funktion aus einem Funktionsgraphen abzulesen, gibt es zwei Möglichkeiten. Entweder du bestimmst zwei Punkte oder du bestimmst einen Punkt und die Steigung. Oft bietet es sich an, den $y$-Achsenabschnitt $n$ direkt abzulesen. Dieser ist hier $n=-1$, da der Graph dort die $y$-Achse schneidet. Da hier die Gitterlinien eingezeichnet sind, kannst du die Steigung ablesen. Gehe dabei so vor:

1. Wähle dir einen Punkt auf dem Graphen, bspw. $(-2|0)$.
2. Gehe um $1$ Einheit nach unten.
3. Gehe so lange nach rechts, bis du den Graphen triffst. Dies sind hier $2$ Einheiten.

Daraus ergibt sich die Steigung $m=-\frac12$. Insgesamt lautet die Funktionsgleichung also $f(x)=-\frac12x-1$.