Muster untersuchen
Muster und Parkettierungen kannst du erkennen, fortführen und spiegeln.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was sind Muster?
Kennst du Mandalas? Das sind Muster in einem Kreis. Ein Muster nennt man eine regelmäßige Anordnung von Formen oder Zeichen. Sie wiederholen sich immer wieder, zum Beispiel Herz – Herz – Herz - Blitz, Herz – Herz - Herz - Blitz, Herz - … Siehst du, wo das Muster anfängt und wo es aufhört? Prima, dann kannst du es sogar selbst fortführen. In der Mathematik gibt es geometrische Muster. Einige werden nur mit dem Zirkel erstellt und sehen ähnlich aus wie ein begonnenes Mandala. In einem Muster sind alle Elemente in gleicher Weise geordnet und sie wiederholen sich. Muster kannst du selbst vervollständigen. Schau dir einmal das Bild unten an. Dieses Muster mit Kästchen hat sechs Reihen. In der siebten Reihe fehlen nun zwei Kästchen. Wo müssen sie ergänzt werden?
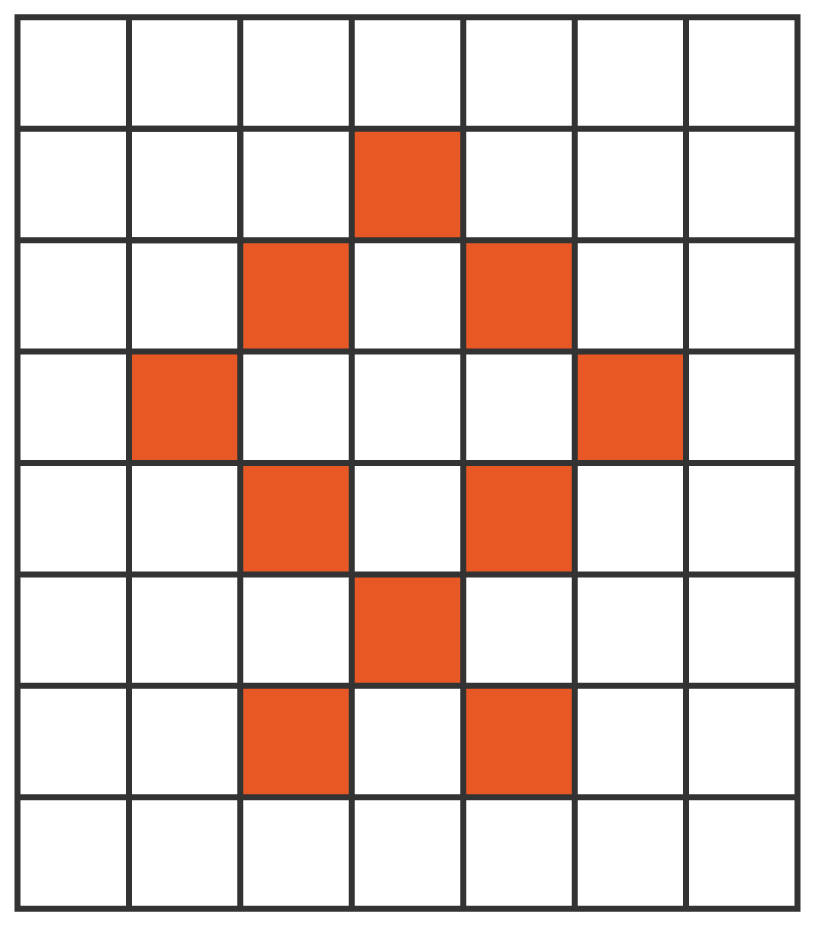
Spiegeln und Symmetrie
Du kannst selbst ein Bild verändern. Male mit Wasserfarben auf ein Blatt Papier. Falte es nun in der Mitte. Klappe es vorsichtig wieder auf. Wie wurde das Bild durch das Falten verändert? Es wurde verdoppelt! Es ist an deiner Faltlinie gespiegelt worden. Das bedeutet, auf beiden Seiten erhältst du das gleiche Bild. Auf die Faltlinie kannst du auch einen Spiegel stellen. Wenn du hineinschaust, sieht dein Bild ganz genauso aus. Es ist wieder auf beiden Seiten gleich. Die Faltlinie nennt man Spiegelachse. Mithilfe dieser kannst du auch selbst ein Spiegelbild zeichnen. Links der Spiegelachse muss alles genauso groß und genauso weit voneinander entfernt sein wie rechts. Das nennt man dann Symmetrie.

Flächen selbst zeichnen
Weißt du schon, was Flächen sind? Alle Flächen haben gemeinsam, dass sie flach sind. Es gibt viele verschiedene, wie zum Beispiel das Rechteck. Das Rechteck hat vier Ecken und die beiden gegenüberliegenden Seiten sind jeweils gleich lang. Auch ein Quadrat hat vier Ecken, es sind jedoch alle vier Seiten gleich lang. Das Dreieck hingegen hat nur drei Ecken. Ein Kreis hat überhaupt keine Ecken und ist daher rund. Mit kariertem Papier, einem Stift und einem Lineal kannst du selbst Flächenformen gestalten. Überlege vorher, wie deine Fläche aussehen soll. Was musst du dabei beachten? Zeichne zuerst Punkte für die Ecken auf das Papier. Verbinde sie nun mit Hilfe eines Lineals. Einen Kreis zeichnest du am besten mit einem Zirkel. Auch um ein umgedrehtes Glas herum kannst du einen Kreis zeichnen. Jetzt kannst du solche Flächenformen auf deinem Papier noch regelmäßig anordnen. So entstehen tolle Muster!
Parkettieren
Einige Formen oder Muster kannst du auch immer wieder direkt aneinander zeichnen. Das kennst du vielleicht von den Steinen vor dem Haus, den Fliesen in eurem Badezimmer oder vom Parkett auf dem Fußboden. Das ist ein Fußbodenbelag aus kleinen Hölzern, die im immer gleichen Muster auf dem Boden verlegt sind. Besonders in alten Villen oder Schlössern ist das sehr aufwändig gemacht. Es dürfen keine Lücken im Muster entstehen. Die Formen dürfen sich auch nicht überlappen. Eine ganze Fläche aus diesen regelmäßigen Mustern nennt man Parkettierung. Auf dem Bild unten siehst du eine Parkettierung.

Welche Formen gibt es? Wie sind sie angeordnet? Werden sie verändert? Kannst du das Muster im Bild erkennen? Dann kannst du das Parkettmuster jetzt vervollständigen. Mit Lili und Niko machen Muster dir bestimmt großen Spaß!
Alle Videos zum Thema
Videos zum Thema
Muster untersuchen (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Muster untersuchen (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen










 Geometrische Muster
Geometrische Muster
 Muster legen
Muster legen
 Wie verändern sich Bilder durch Falten?
Wie verändern sich Bilder durch Falten?
 Flächenformen gestalten
Flächenformen gestalten
 Flächen parkettieren
Flächen parkettieren









