Dreiecke

Inhaltsverzeichnis zum Thema

• Was ist ein Dreieck?
• Merkmale eines Dreiecks
• Der Winkelsummensatz
• Der Umfang eines Dreiecks
• Die Fläche eines Dreiecks
• Verschiedene Arten von Dreiecken
• Winkelarten
• Spitzwinklige Dreiecke
• Rechtwinklige Dreiecke
• Stumpfwinklige Dreiecke
• Gleichschenklige Dreiecke
• Gleichseitige Dreiecke

Was ist ein Dreieck?

Merkmale eines Dreiecks

Ein Dreieck ist eine ebene Figur.

• Ein Dreieck hat, wie du an dem Namen bereits erkennen kannst, drei Ecken. Diese werden gegen den Uhrzeigersinn mit den Großbuchstaben $A$, $B$ und $C$ bezeichnet.
• Die den Punkten gegenüberliegenden Seiten werden mit den entsprechenden Kleinbuchstaben $a$, $b$ und $c$ bezeichnet.
• Die drei Winkel eines Dreiecks sind zu erkennen an den griechischen Buchstaben $\alpha$ (alpha) für a, $\beta$ (beta) für b und $\gamma$ (gamma) für $c$.

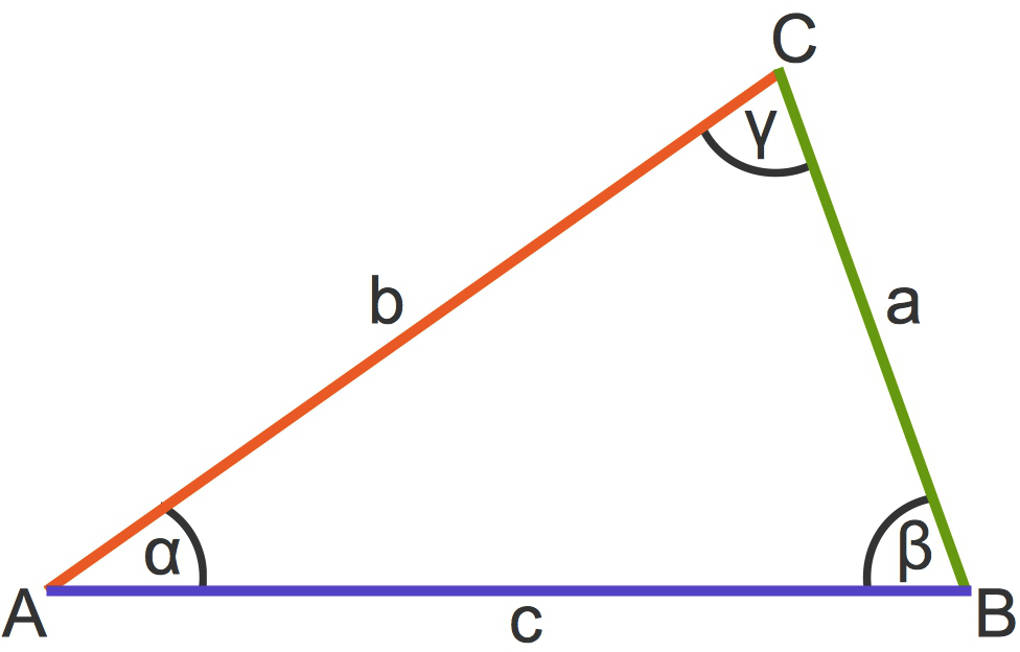
Der Winkelsummensatz

In jedem beliebigen Dreieck gilt der Winkelsummensatz: Die Summe der Innenwinkel eines Dreiecks beträgt $180^\circ$.

$\alpha+\beta+\gamma=180^\circ$

Wenn du die Größen von zwei Winkeln im Dreieck kennst, kannst du mit dem Winkelsummensatz immer die Größe des dritten Winkels ausrechnen.

Der Umfang eines Dreiecks

Der Umfang eines Dreiecks ist gegeben durch die Summe der Seiten.

$U=a+b+c$

Die Fläche eines Dreiecks

Um die Fläche eines Dreiecks zu berechnen, benötigst du die Höhe, die der Abstand von einer Seite und dem gegenüberliegenden Punkt ist. Ein Dreieck hat somit drei Höhen, $h_a$, $h_b$ und $h_c$. Diese erhältst du, indem du von einem Punkt das Lot auf die gegenüberliegende Seite fällst. Hier siehst du das obige Dreieck mit der Höhe $h_c$.

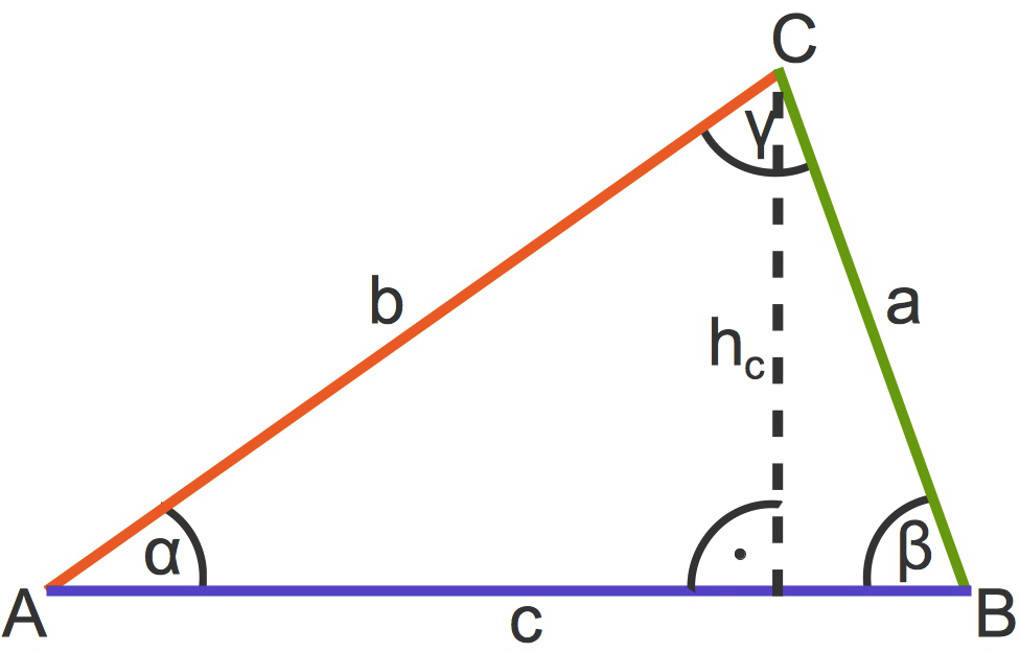
Die Fläche ist dann gegeben durch die Formel

$A=\frac{c\cdot h_c}2=\frac{a\cdot h_a}2=\frac{b\cdot h_b}2$.

Verschiedene Arten von Dreiecken

Winkelarten

Da die Summe der drei Innenwinkel immer $180^\circ$ ergibt, kann keiner der Winkel größer oder gleich $180^\circ$ sein. Du kannst die folgenden Winkel unterscheiden:

• Ein Winkel von genau $0^\circ$ ist ein Nullwinkel.
• Ein Winkel, der kleiner ist als $90^\circ$, wird als spitzer Winkel bezeichnet.
• Der $90^\circ$-Winkel wird als rechter Winkel bezeichnet.
• Ein Winkel, der größer ist als $90^\circ$ und kleiner als $180^\circ$, wird als stumpfer Winkel bezeichnet.
• Ein Winkel von genau $180^\circ$ ist ein getreckter Winkel.
• Ist ein Winkel größer als $180^\circ$ und kleiner als $360^\circ$, wird er als überstumpfer Winkel bezeichnet.
• Ein Winkel von genau $360^\circ$ ist ein Vollwinkel.

Es gibt verschiedene Arten von Dreiecken.

Spitzwinklige Dreiecke

Wenn in einem Dreieck alle drei Winkel spitze Winkel sind, so wird dieses Dreieck als spitzwinkliges Dreieck bezeichnet.

Rechtwinklige Dreiecke

Wenn ein Dreieck einen rechten Winkel besitzt, dann wird dieses Dreieck als rechtwinkliges Dreieck bezeichnet.

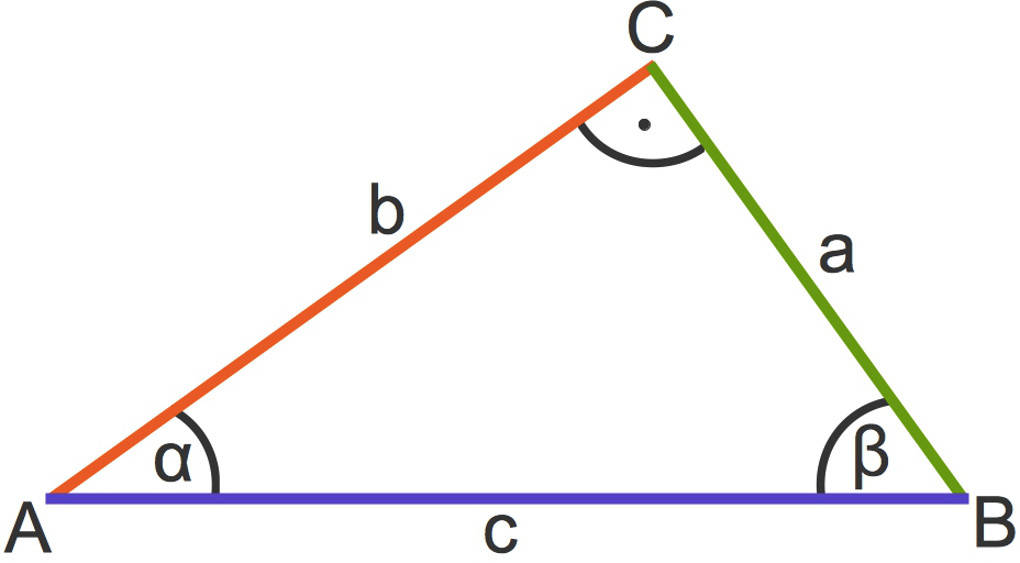
Den rechten Winkel erkennst du an dem Punkt. Gegenüber von dem rechten Winkel befindet sich die längste Seite des rechtwinkligen Dreiecks, die Hypotenuse, hier $c$. Die beiden übrigen Seiten, $a$ und $b$, liegen an dem rechten Winkel an. Dies sind die Katheten.

Da in einem rechtwinkligen Dreieck ein Winkel $90^\circ$ beträgt, gilt

• zum einen, dass die beiden anderen Winkel spitze Winkel sind und
• zum anderen, dass die Summe dieser beiden Winkel $90^\circ$ beträgt.

Rechtwinklige Dreiecke sind von besonderer Bedeutung:

• Es gilt der Satz des Pythagoras.
• In rechtwinkligen Dreiecken kannst du den Kathetensatz und Höhensatz anwenden.
• Die trigonometrischen Funktionen Sinus, Kosinus und Tangens sind in rechtwinkligen Dreiecken definiert.

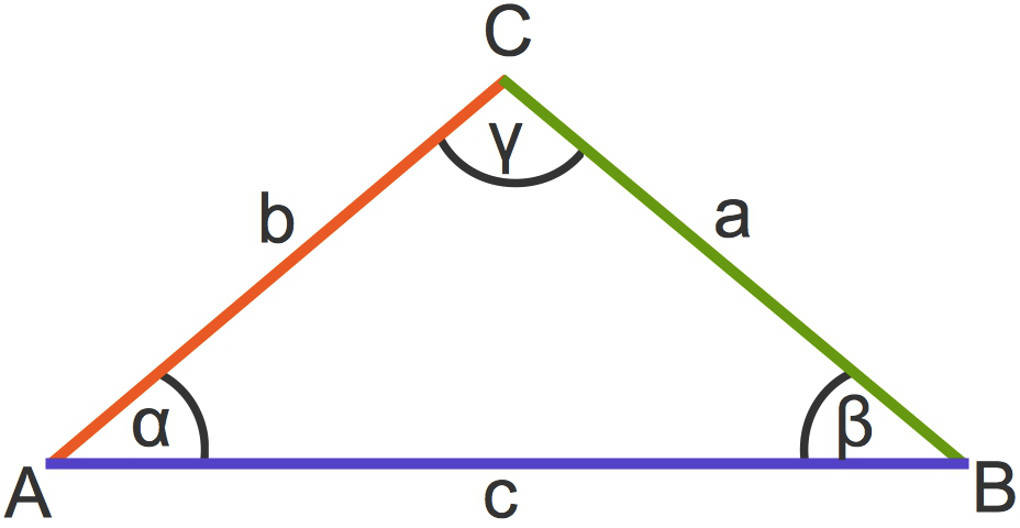
Stumpfwinklige Dreiecke

Wenn ein Dreieck einen stumpfen Winkel besitzt, dann wird dieses Dreieck als stumpfwinkliges Dreieck bezeichnet. Wegen des Winkelsummensatzes gilt, dass ein Dreieck höchstens einen stumpfen Winkel besitzen kann.

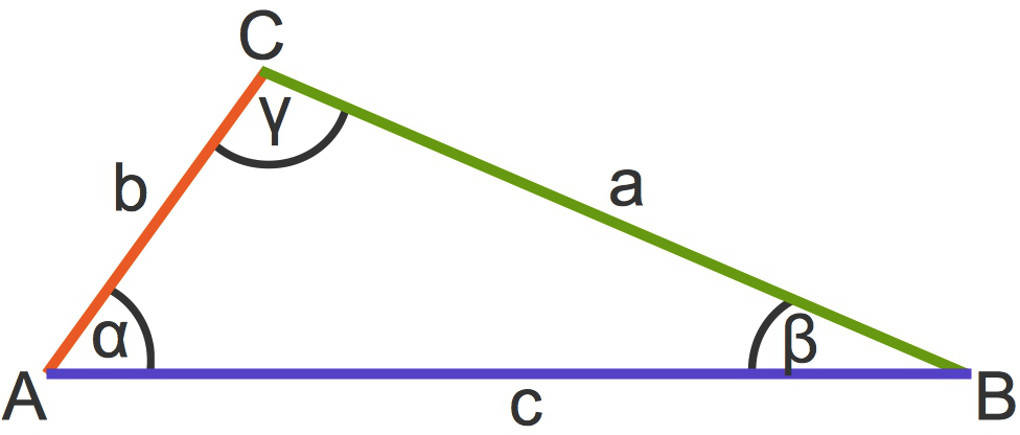
Gleichschenklige Dreiecke

Ein gleichschenkliges Dreieck hat mindestens zwei gleich lange Seiten. Diese beiden gleichlangen Seiten werden als Schenkel bezeichnet. Die dritte Seite ist die Basis. Die beiden Winkel, die an der Basis anliegen, also den Schenkeln gegenüberliegen, werden als Basiswinkel bezeichnet.

• Die beiden Schenkel sind $a$ und $b$.
• Die Basis ist $c$.
• Die Basiswinkel sind $\alpha$ und $\beta$.

In gleichschenkligen Dreiecken gilt der Basiswinkelsatz. Dieser besagt, dass die beiden Basiswinkel gleich groß sind.

Gleichseitige Dreiecke

Wenn in einem Dreieck alle drei Seiten gleich lang sind, wird dieses Dreieck gleichseitiges Dreieck genannt.

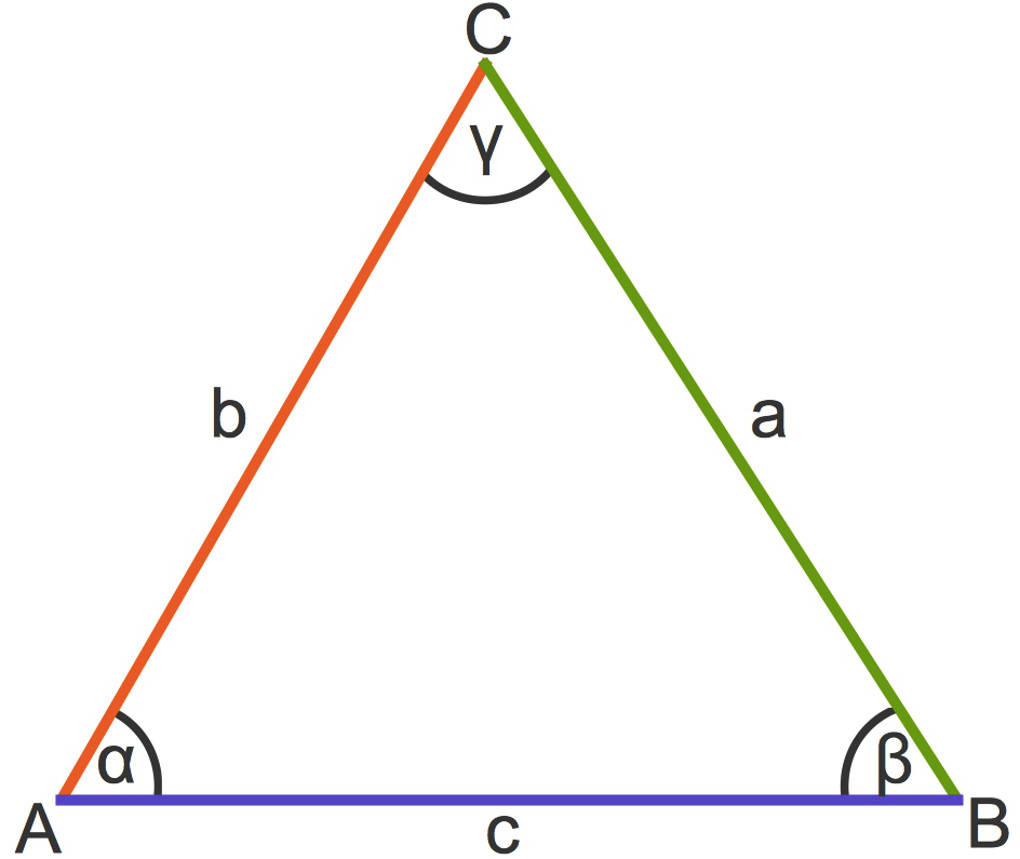
Da alle drei Seiten gleich lang sind, sind auch alle Winkel gleich groß. Mit dem Winkelsummensatz kannst du dann schließen, dass alle drei Winkel $60^\circ$ betragen.

Übrigens: Jedes gleichseitige Dreieck ist auch gleichschenklig. Umgekehrt ist jedoch nicht jedes gleichschenklige Dreieck gleichseitig.