Kreuzprodukt
Das Kreuzprodukt wird auch als vektorielles Produkt, Vektorprodukt oder äußeres Produkt bezeichnet. Es ist das "Produkt" zweier Vektoren und stellt selbst einen Vektor dar, welcher orthogonal zu diesen ist.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Vektor?
- Was ist ein Kreuzprodukt?
- Ein Trick zur Berechnung des Kreuzproduktes
- Anwendung des Kreuzproduktes
- Flächenberechnung Parallelogramm
- Flächenberechnung Dreieck
- Volumenberechnung Spat
Was ist ein Vektor?
Ein Vektor, zum Beispiel $\vec a$, in dem euklidischen Raum $\mathbb{R}^3$ hat drei Koordinaten. Diese Koordinaten werden entweder mit den Indizes $1$, $2$, $3$ oder auch mit $x$, $y$, $z$ bezeichnet und spaltenweise aufgeschrieben. Der Vektor $\vec a$ sieht im $\mathbb{R}^3$ so aus:
$\vec a=\begin{pmatrix} a_1 \\ a_2\\ a_3 \end{pmatrix}=\begin{pmatrix} a_x \\ a_y\\ a_z \end{pmatrix}$.
Das Kreuzprodukt ist nur für Vektoren im $\mathbb{R}^3$ definiert.
Was ist ein Kreuzprodukt?
Du kennst vielleicht bereits
- die skalare Multiplikation, hier wird ein Vektor mit einem Skalar, also einer Zahl multipliziert, das Ergebnis ist ein Vektor
$\quad~~~3\cdot \begin{pmatrix} 1 \\ 3\\ -2 \end{pmatrix}=\begin{pmatrix} 3\cdot 1 \\ 3\cdot 3\\ 3\cdot (-2) \end{pmatrix}=\begin{pmatrix} 3 \\ 9\\ -6 \end{pmatrix}$
- oder das Skalarprodukt zweier Vektoren, das Ergebnis ist ein Skalar, oder eine Zahl: $\vec a\cdot \vec b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z$.
Das Kreuzprodukt hat als Ergebnis einen Vektor. Daher kommt der Name. Es wird auch als vektorielles Produkt, Vektorprodukt oder äußeres Produkt bezeichnet.
Das Kreuzprodukt zweier Vektoren ist wie folgt definiert:
$\vec a\times\vec b=\begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}\times\begin{pmatrix} b_x \\ b_y \\ b_z\end{pmatrix}=\begin{pmatrix} a_y\cdot b_z-a_z\cdot b_y \\ a_z\cdot b_x-a_x\cdot b_z\\ a_x\cdot b_y-a_y\cdot b_x \end{pmatrix}$.
Ein Trick zur Berechnung des Kreuzproduktes
Die obige Definition sieht recht kompliziert aus. Du kannst mit einem einfachen Trick das Vektor- oder auch Kreuzprodukt zweier Vektoren berechnen. Dies siehst du hier an einem Beispiel. Berechnet werden soll das Kreuzprodukt der beiden Vektoren $\vec a$ und $\vec b$, für die gilt:
$\vec a=\begin{pmatrix} 3 \\ 4\\ 1 \end{pmatrix}$
sowie
$\vec b=\begin{pmatrix} 2\\ -1 \\ 2 \end{pmatrix}$.
Dann kannst du das Kreuzprodukt folgendermaßen berechnen.
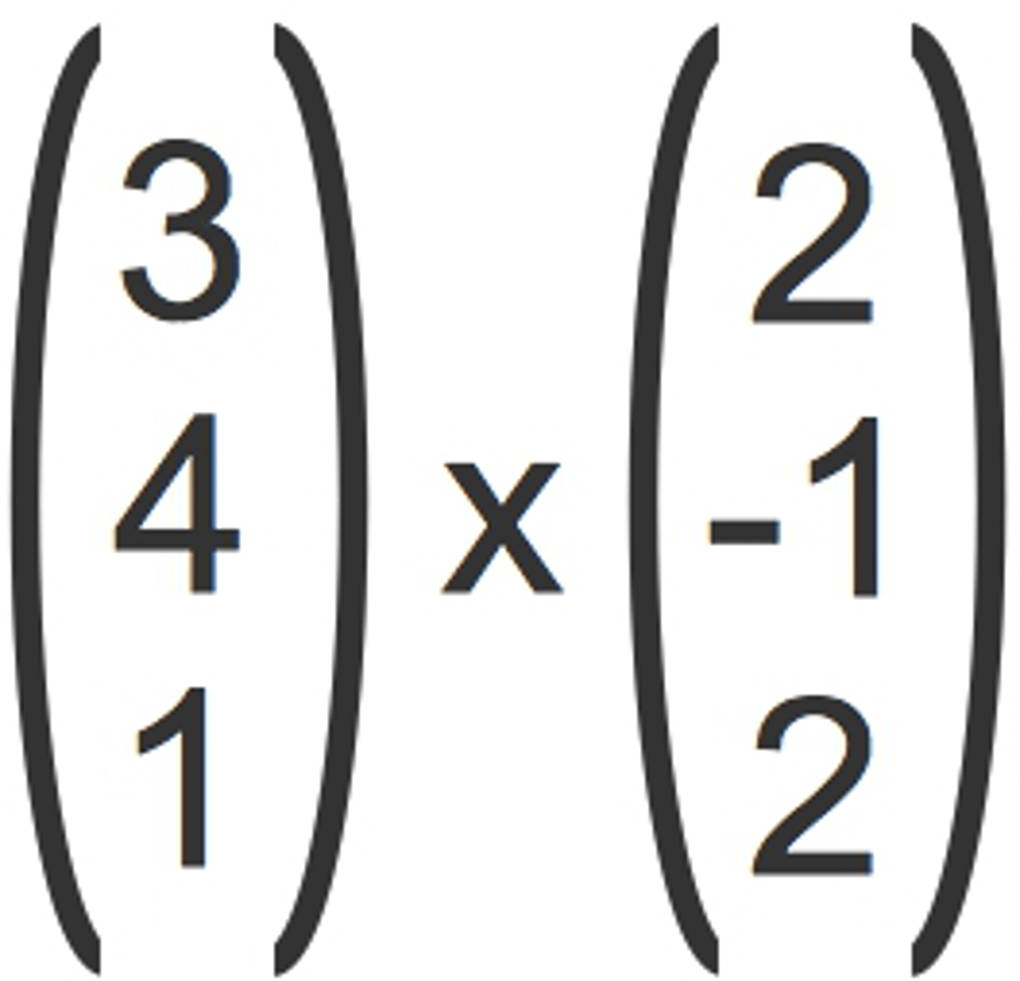
- Schreibe zunächst die jeweils ersten beiden Koordinaten der Vektoren noch einmal unter die Vektoren.
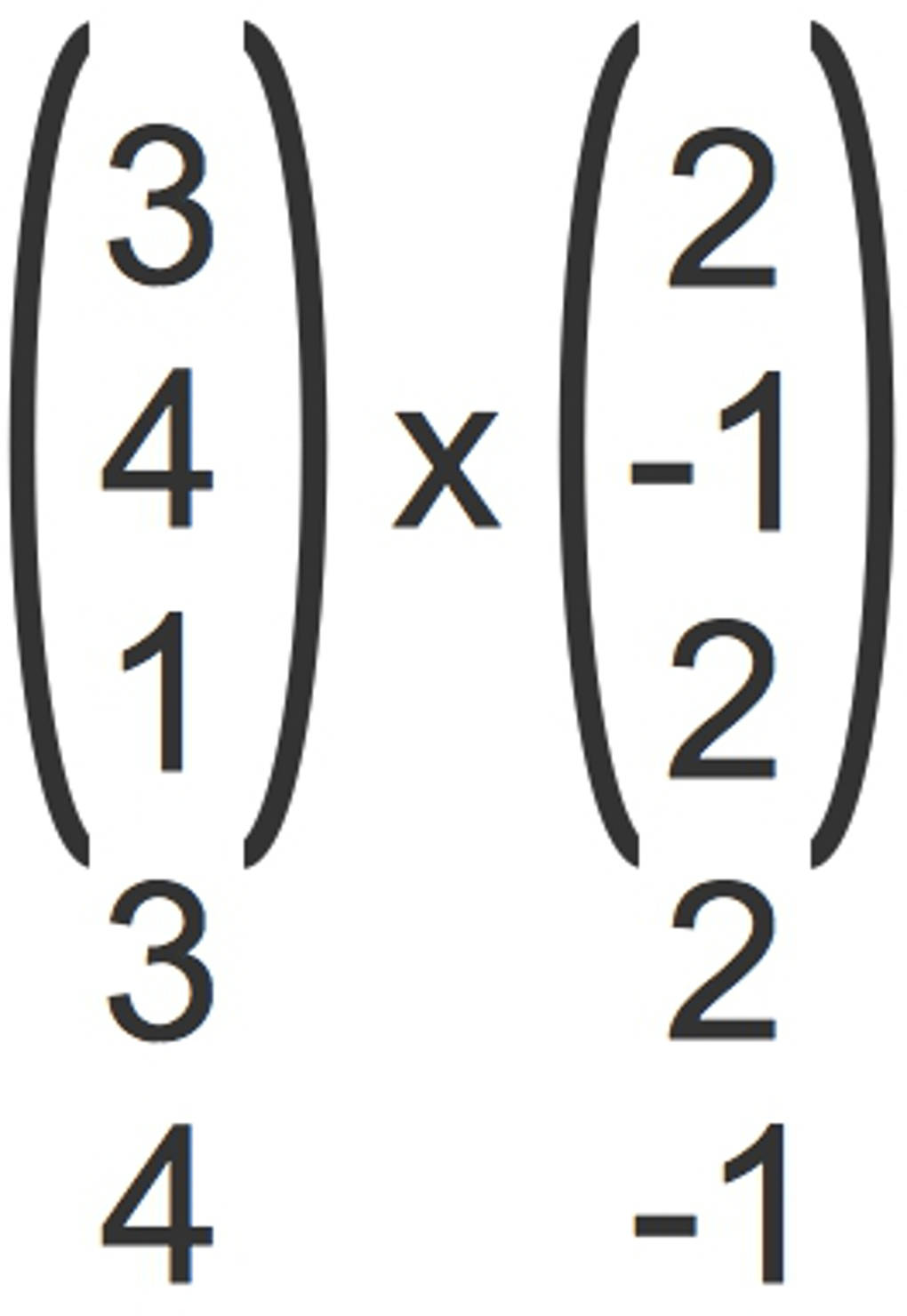
- Nun kannst du Koordinate für Koordinate das Kreuzprodukt berechnen, das bedeutet die Koordinaten des resultierenden Vektors.
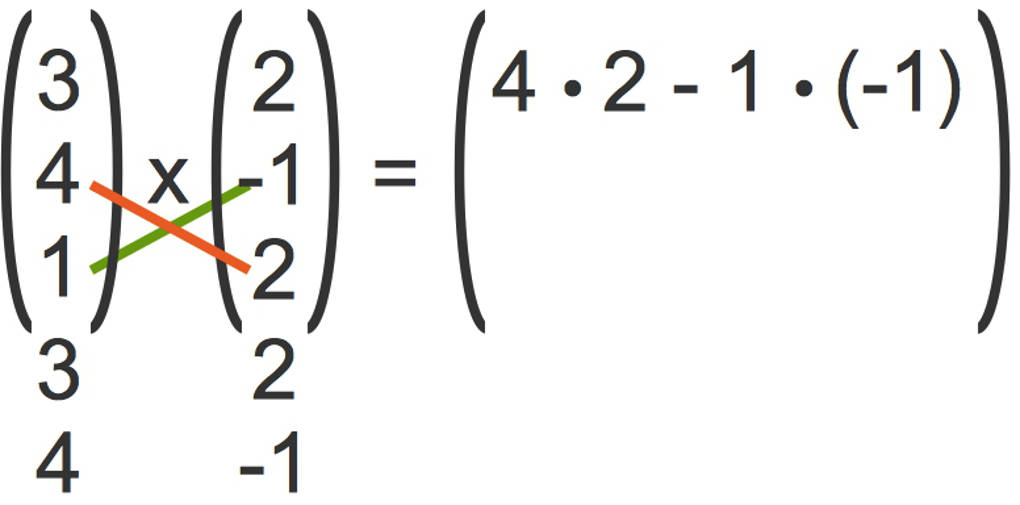
- Multipliziere die Koordinaten von links oben nach rechts unten (hier rot) und ziehe davon das Produkt der Koordinaten von links unten nach rechts oben (hier grün) ab.
- Ebenso machst du dies mit den nächsten beiden Koordinaten. Das siehst du hier:
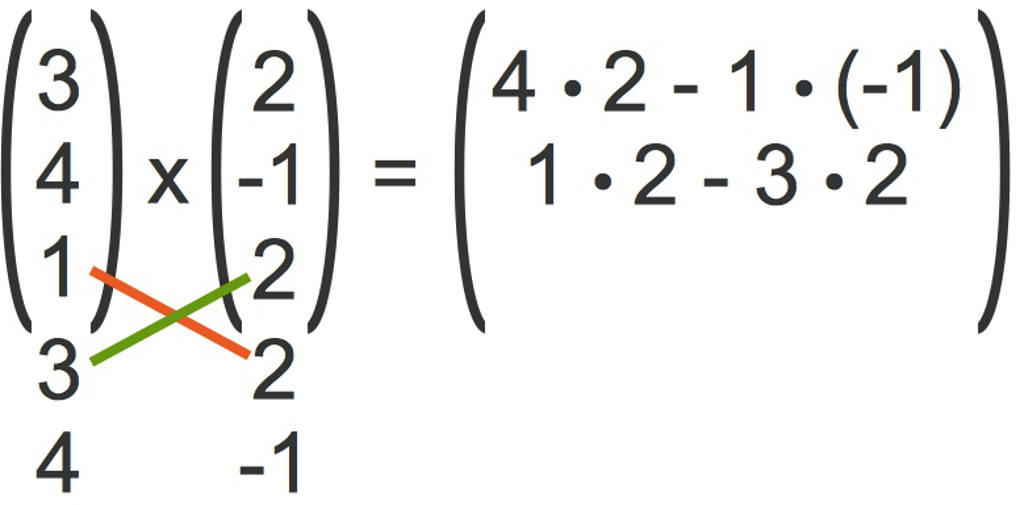
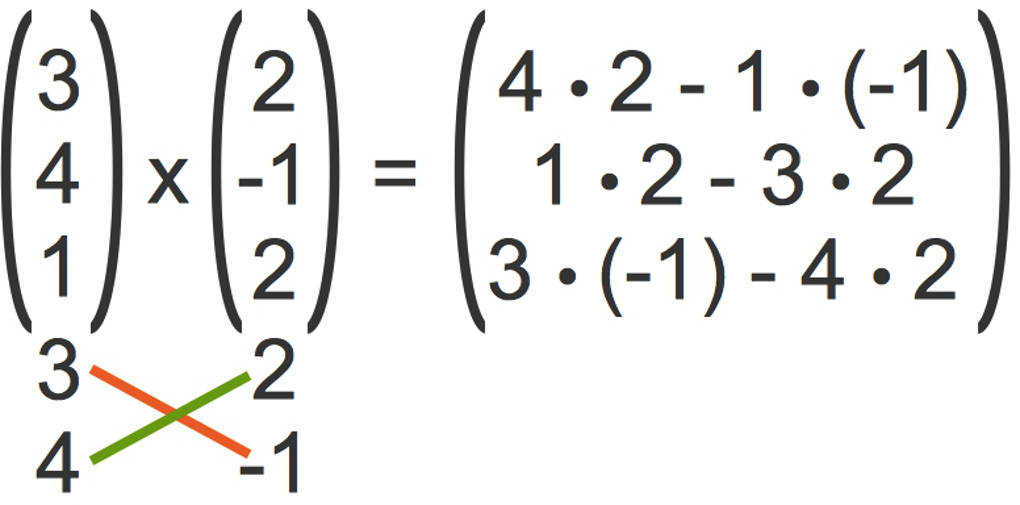
- Zuletzt berechnest du die jeweiligen Differenzen.
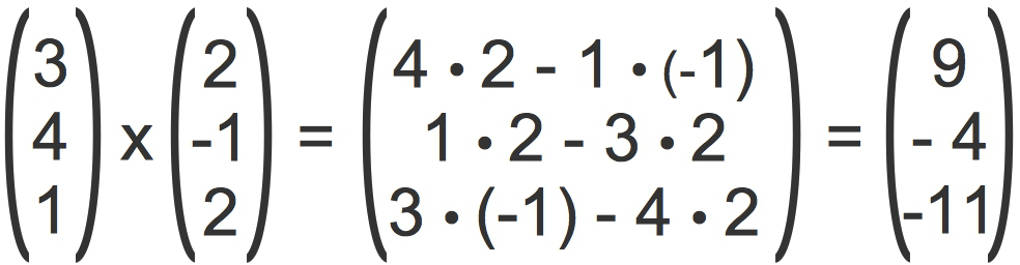
Du hast damit das Kreuzprodukt berechnet.
$\begin{pmatrix} 3 \\ 4 \\ 1 \end{pmatrix}\times\begin{pmatrix} 2 \\ -1 \\ 2\end{pmatrix}=\begin{pmatrix} 9 \\ -4\\ -11 \end{pmatrix}$
Wofür benötigst du eigentlich das Kreuzprodukt?
Wenn du den Ergebnisvektor mit jedem der beiden Vektoren multiplizierst, erhältst du
$\begin{pmatrix} 3 \\ 4 \\ 1 \end{pmatrix}\cdot\begin{pmatrix} 9 \\ -4\\ -11 \end{pmatrix}=27-16-11=0$
sowie
$\begin{pmatrix} 2 \\ -1 \\ 2\end{pmatrix}\cdot\begin{pmatrix} 9 \\ -4\\ -11 \end{pmatrix}=18+4-22=0$.
Wenn das Skalarprodukt zweier Vektoren $0$ ergibt, bedeutet dies, dass die Vektoren orthogonal, also senkrecht, zueinander sind.
Der resultierende Vektor des Kreuzproduktes zweier Vektoren $\vec a$ und $\vec b$ steht also senkrecht auf den beiden Vektoren. Es gilt:
- $\vec a\times\vec b\perp \vec a$ und
- $\vec a\times\vec b\perp \vec b$.
Wenn durch die beiden Vektoren $\vec a$ und $\vec b$ eine Ebene aufgespannt wird, steht also der aus dem Kreuzprodukt resultierende Vektor senkrecht zu der Ebene. Man bezeichnet den Vektor dann als Normalenvektor der Ebene. Dieser Vektor wird mit $\vec n$ bezeichnet.
Anwendung des Kreuzproduktes
Flächenberechnung Parallelogramm
Die Fläche eines Parallelogramms kannst du mit Hilfe des Skalarproduktes berechnen. Etwas kompakter ist die Berechnung mit Hilfe des Kreuzprodukt.
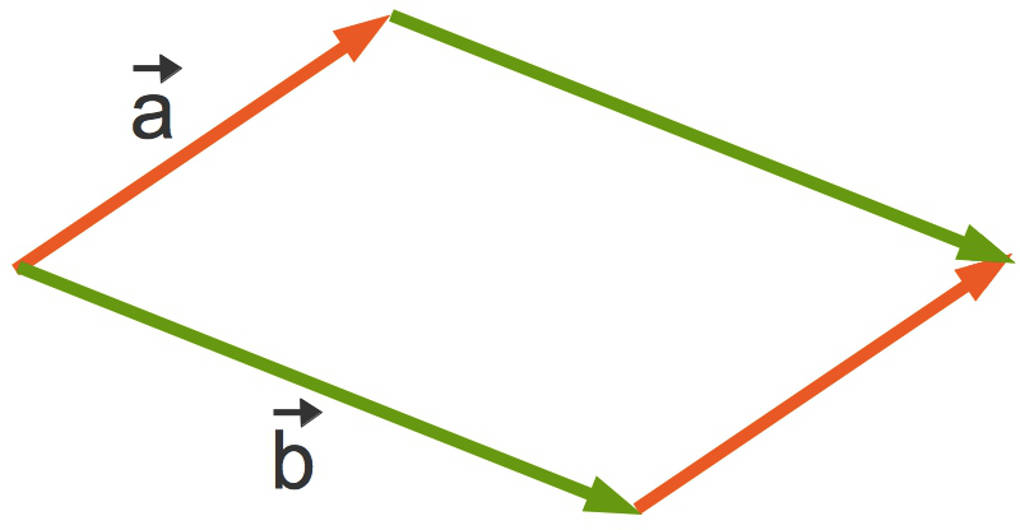
$A_{\text{Parallelogramm}}=\left|\vec a\times \vec b\right|$
Dabei stehen die Betragsstriche für den Betrag oder die Länge des Vektors.
Flächenberechnung Dreieck
Die Fläche eines Dreiecks lässt sich ebenfalls mit der obigen Formel berechnen. Du musst noch durch $2$ dividieren.
$A_{\text{Dreieck}}=\frac12\cdot\left|\vec a\times \vec b\right|$
Dies können wir an einem Beispiel üben.
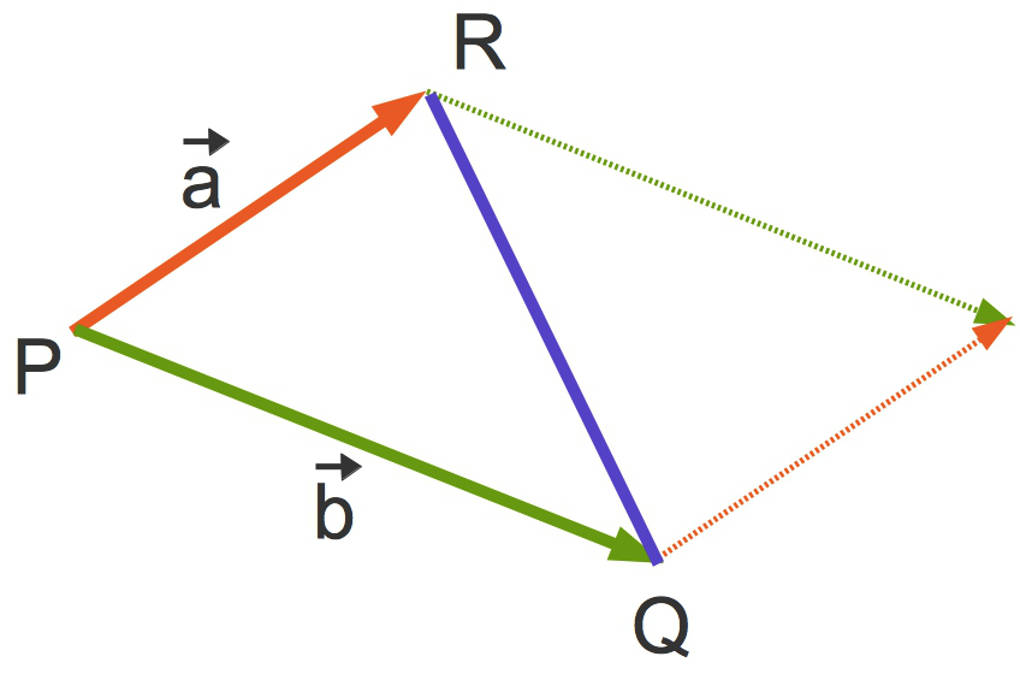
Die Punkte seien $P(3|2|1)$, $Q(1|-1|-3)$ sowie $R(-2|2|2)$.
- $\vec a=\vec{PR}=\begin{pmatrix} -5 \\ 0\\ 1 \end{pmatrix}$
- $\vec b=\vec{PQ}=\begin{pmatrix} -2 \\ -3\\ -4 \end{pmatrix}$
- $\begin{pmatrix} -5 \\ 0 \\ -1\end{pmatrix}\times\begin{pmatrix} -2 \\ -3\\ -4 \end{pmatrix}=\begin{pmatrix} 0-3 \\ 2-20\\ 15-0 \end{pmatrix}=\begin{pmatrix} -3 \\ -18\\ 15 \end{pmatrix}$
Nun kannst du den Flächeninhalt des Dreiecks $\Delta_{PQR}$ berechnen.
$\begin{array}{rcl}A_{\Delta_{PQR}}&=&\frac12\left|\begin{pmatrix} -3 \\ -18\\ 15 \end{pmatrix}\right|\\ &=&\frac12\cdot \sqrt{9+324+225}\\ &=&\frac12\cdot\sqrt{558}\\ &\approx&11,8 ~\text{[FE]}\end{array}$
Volumenberechnung Spat
Ein Spat oder auch Parallelepiped ist ein geometrischer Körper. Die begrenzenden Flächen sind paarweise kongruente, in parallelen Ebenen liegende Parallelogramme. Hier siehst du ein Spat.
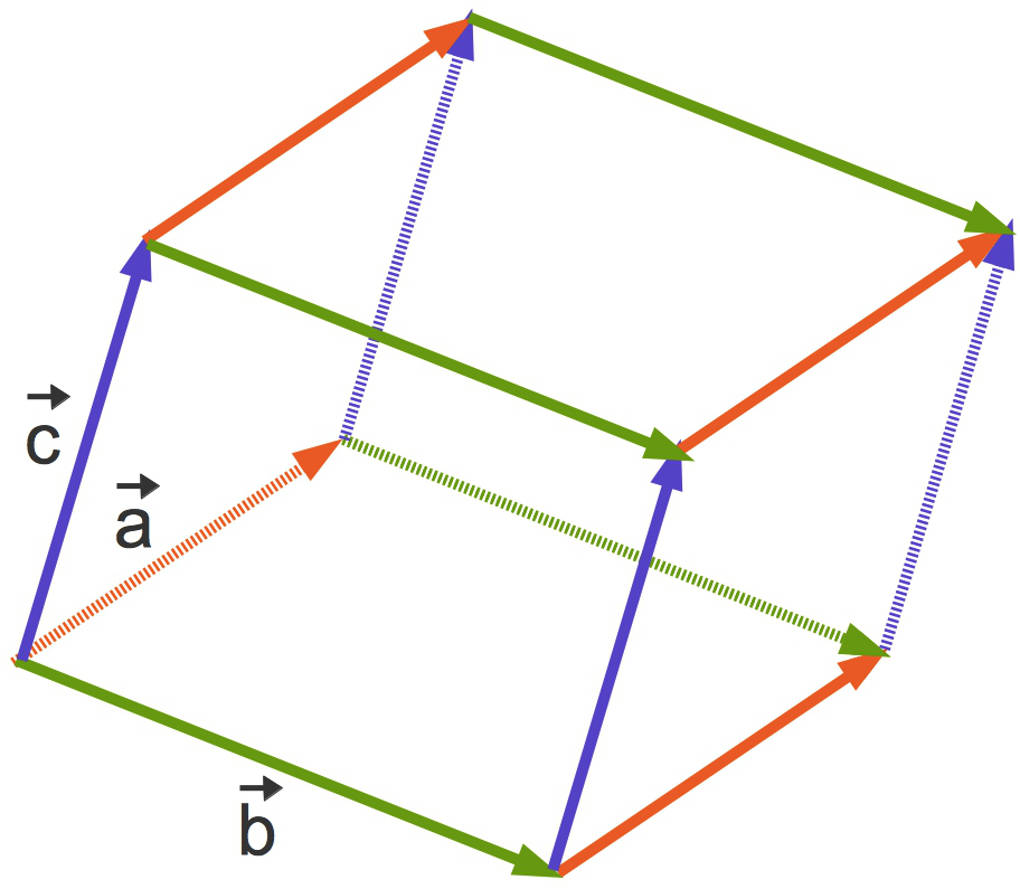
Dieser Spat wird von den drei Vektoren $\vec a$, $\vec b$ und $\vec c$ aufgespannt.
Das Volumen eines solchen Spats ist gegeben durch das Spatprodukt:
$V_{\text{Spat}}=\left|\left(\vec a\times\vec b\right)\cdot \vec c\right| $.
Alle Videos zum Thema
Videos zum Thema
Kreuzprodukt (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Kreuzprodukt (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter









 Kreuzprodukt – Definition
Kreuzprodukt – Definition
 Anwendung des Kreuzprodukts
Anwendung des Kreuzprodukts
 Anwendung des Kreuzprodukts – Beispiele
Anwendung des Kreuzprodukts – Beispiele
 Kreuzprodukt – Herleitung
Kreuzprodukt – Herleitung












