Mathematische Beschreibung gedämpfter elektromagnetischer Schwingungen

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Mathematische Beschreibung gedämpfter elektromagnetischer Schwingungen
In diesem Video wird dir erklärt, wie gedämpfte elektromagnetische Schwingungen mathematisch beschrieben werden können. Ausgehend vom ungedämpften Fall wird an Hand von Energiebilanzen eine Differentialgleichung für den gedämpften Fall aufgestellt. Eine Strukturbetrachtung dieser Gleichung erinnert an die Lösung der entsprechenden Differentialgleichung der gedämpften Pendelschwingung aus der Mechanik. Damit ist ein Lösungsansatz gefunden, der zur mathematischen Beschreibung der gedämpften elektromagnetischen Schwingungen führt. Im I-t-Diagramm wird der Verlauf der gedämpften Schwingung beschrieben. Zum Schluss werden Kreisfrequenz und Frequenz von ungedämpfter und gedämpfter Schwingung verglichen.
Transkript Mathematische Beschreibung gedämpfter elektromagnetischer Schwingungen
Hallo, hier ist wieder Dr. Psi. Unser heutiges Thema ist die mathematische Behandlung elektromagnetischer Schwingungen. Zuerst erinnern wir uns an den Schwingkreis, an den Aufbau des Schwingkreises. Für ungedämpfte elektromagnetische Schwingungen und wollen dann die Erzeugung ungedämpfter Schwingungen kurz beschreiben. Dann wollen wir uns die Energiebilanz der elektromagnetischen Schwingungen anschauen. Und genau diese Energiebilanz führt uns auf die Erzeugung gedämpfter elektromagnetischer Schwingungen. Wir werden uns daran erinnern, dass für diese Art von Schwingungen bereits ein Lösungsansatz existiert. Diesen Lösungsansatz wollen wir beschreiten und aufgrund der daraus abgeleiteten Lösung einer Beschreibung eben der gedämpften elektromagnetischen Schwingung herleiten. Nachdem wir einige Formeln dazu uns angesehen haben, werden wir die Formeln von gedämpfter und ungedämpfter Schwingung miteinander vergleichen und schließlich zum Schluss das Gelernte zusammenfassen. Machen wir uns also auf den Weg durch ein etwas kompliziertes Gebiet. Aber keine Angst, wir schaffen das. Wir werden jeden Schritt ausführlich erklären. Hier ist also unser Schwingkreis. Wir sehen eine Spannungsquelle, einen Kondensator, eine Spule und einen Schalter, der zunächst offen ist. Um den Schwingkreis hinsichtlich Strom und Spannung zu untersuchen sind entsprechende Messgeräte eingebaut. Wir sehen uns nun an wie ungedämpfte Schwingungen erzeugt werden. Ein Blick auf den Schwingkreis zeigt uns, dass zur Erzeugung ungedämpfter Schwingungen der Schalter S so geschaltet werden muss, dass zwischen S und Kondensator eine Verbindung besteht. Der Kondensator muss aufgeladen werden. In diesem Fall fließt kein Strom, I ist gleich Null. Und wir sehen, dass in dem I über T Diagramm an der Stelle T gleich Null. Das ist unser Ausgangspunkt für die Beschreibung der elektromagnetischen Schwingung. Nun wird der Schalter umgelegt und der Kondensator entlädt sich. Das bedeutet, die Spannung U geht gegen Null und die Stromstärke I wird maximal. Wir sehen, dass in unserem Schaubild das die Stromstärke anwächst, aber die Richtung zeigt nach unten. Das hängt damit zusammen, dass der Kondensator und die Spannungsquelle genauso geschaltet sind, dass der Betrag der Stromstärke maximal wird, aber die Richtung ist so wie sie hier eingezeichnet wird. Also bei T/4 befinden wir uns an der Stelle des Minimums genau an dieser Stelle. Wenn der Strom maximal ist, ist die Spule von diesem Strom durchsetzt, wir finden dort ein Magnetfeld und dieses Magnetfeld ist in diesem Augenblick maximal. Nach der Zeit T/2 bricht dieses Magnetfeld zusammen und der Strom, der in dem Schwingkreis fließt wird, wenn wir uns dieses Bild angucken, das Minimum verlassen und an der Stelle T/2 entsteht wieder der Punkt I gleich Null und T gleich 1/2. Wir beobachten also hier B bricht zusammen. Der Strom fließt in diese Richtung und lädt dabei den Kondensator wieder auf. Der Kondensator wird wieder auf U gleich U max. aufgeladen, der Strom fließt, wird grösser in eine andere Richtung. Dieser Vorgang wiederholt sich. Und was haben wir da? Ja klar, wenn wir diesen Vorgang auf unserem Bild sehen, haben wir eine Schwingung. Genau das wollten wir ja haben. Wir kennen unserer ungedämpften elektromagnetischen Schwingung ein paar physikalische Größen. Das sind zum Beispiel die Periodendauer T gleich 2 Pi Wurzel L mal C, L war die Induktivität und C die Kapazität. Dann kennen wir die Frequenz, die ist 1/T also 1 durch 2 Pi mal Wurzel L mal C und schließlich die Kreisfrequenz Omega gleich 1 durch Wurzel L C. Nun wollen die Energiebilanzen von ungedämpfter und gedämpfter Schwingung miteinander vergleichen. Wir sind zunächst beim ungedämpften Schwingkreis. Wir haben gesehen, dass die Energie sich im Kondensator befindet, das ist die elektrische Energie. Dann bricht das Feld im Kondensator zusammen und es entsteht ein Strom, der ein Magnetfeld in der Spule aufbaut. Das heißt, elektrische und magnetische Energie wechseln sich einander ab. Aber die magnetische Energie und die elektrische Energie sind in der Summe konstant. Das ist der Fall des ungedämpften Schwingkreises. Nun schauen wir uns den gedämpften Schwingkreis an. Wir notieren noch einmal an dieser Stelle den ungedämpften Schwingkreis. Im gedämpften Fall haben natürlich auch wieder ein Magnetfeld und ein elektrisches Feld. Wir können also wieder notieren E magnetisch plus E elektrisch. Aber jetzt kommt noch etwas dazu. Wenn hier ein Strom fließt, dann wird natürlich das auf die Leitung sich auswirken. Die Leitungen werden sich erwärmen. Die Wärme wird an die Umwelt abgegeben und geht dem Schwingkreis verloren. Und das ist natürlich der Fall, dass wir beobachten die Schwingungen im Verlauf der Zeit gedämpft wird. Und dieser Fall wird dadurch berücksichtigt, dass wir hier eine Energie hinzufügen, die ... und wir haben hier den Index R, steht für Ohmschen Widerstand des gesamten Schwingkreises... da geht einige Energie rein. Insgesamt bleibt aber die Energie konstant. Das ist also der gedämpfte Fall. Was fangen wir nun mit unserer schönen Formel an? Wir müssen uns jetzt in einem nächsten Schritt überlegen, wie wir aus diesen Formeln E magnetisch, E elektrisch ein wenig zum Schwingkreis übergehen. Dort haben wir die physikalischen Größen L Induktivität, C Kapazität. Und dies wollen wir hier einsetzen. Dabei wollen wir uns daran erinnern wie der Zusammenhang zwischen diesen Größen und der Energie ist. Das können wir entweder dadurch machen, dass ihr euch in eurem Kopf mal umseht, welche Formeln da existieren oder ihr guckt in eine Formelsammlung. Dies nehme ich euch mal ab. Wir erinnern uns, dass die magnetische Energie die Form hat 1 durch 2 mal L mal Q Punkt Quadrat. Die Energie, die über die Ohmschen Widerstände sich definiert lassen wir erstmal stehen. Die elektrische Energie, die ist gegeben durch 1 durch 2 C mal Q Quadrat. Und das Ganze ist konstant. Hier steht die Formel, die uns interessiert. Diese Formel wollen jetzt nach der Zeit ableiten. Dazu brauchen wir noch ein paar Kenntnisse aus dem Mathematikunterricht. Wenn wir das nach der Zeit ableiten und ich erinnere noch einmal daran, Q ist eigentlich mit dem Argument t versehen, genauso wie E. Wir haben das Argument weggelassen aus Platzgründen, damit es hier übersichtlicher bleibt. Das nach der Zeit abgeleitet, die 2 Punkt nach vorne kürze ich weg, es bleibt L mal Q Punkt. Und die innere Ableitung von Q Punkt wäre dann Q zwei Punkt plus hier notieren wir einfach die zeitliche Ableitung durch den Punkt. Der dritte Term zeitlich abgeleitet ergibt die zwei wieder nach vorne, es bleibt 1 durch C mal Q Punkt mal, und ich habe jetzt die Reihenfolge vertauscht, Q mal Q Punkt. Und wenn wir jetzt hier die Konstante ableiten, Konstante abgeleitet ergibt Null. Klar. Nun schauen wir uns mal diesen Term an, den müssen wir etwas näher betrachten. Die zeitliche Ableitung der Energie ist die Leistung. Also können wir notieren: ER Punkt gleich Leistung P, das ist bekanntlich U mal I oder anders geschrieben R mal I Quadrat. Und wenn wir jetzt noch den Zusammenhang zwischen I und der Ladung, du erinnerst dich sicherlich, I ist gleich Q durch T, wenn wir das berücksichtigen, können wir auch schreiben R mal Q Punkt zum Quadrat. Diesen Term setzen wir in unsere Formel ein und erhalten: L mal Q Punkt mal Q zwei Punkt plus. Jetzt berücksichtigen wir diesen Term: R mal Q Punkt zum Quadrat plus 1 durch C, Q Punkt mal Q gleich Null. Was fällt bei dieser Formel auf? Wir haben in jedem dieser Terme Q Punkte stehen und das wollen wir einfach einmal ausklammern. Wir erhalten Q Punkt mal in Klammern L mal Q zwei Punkt plus einmal von diesem Q Punkt Quadrat geht nach vorne, also R mal Q Punkt plus 1 durch C mal Q Punkt ausgeklammert. Es bleibt übrig: Q Klammer zu gleich Null. Hier steht ein Produkt aus zwei Faktoren. Der erste Faktor ist Q Punkt, hängt mit I zusammen. Das wissen wir nun inzwischen. Und wir sehen, dass dieser Faktor nicht immer gleich Null ist. Folglich muss der zweite Faktor gleich Null sein. Wir notieren den, dividieren aber diesen Faktor insgesamt gleich durch L, dann bleibt hier übrig Q zwei Punkt plus Division des gesamten Faktors durch L, also R durch L mal Q Punkt plus, werden auch hier wieder den Faktor L berücksichtigen, L mal C mal Q gleich Null. Dieser Lösungsansatz, immer daran denken, wir haben Y durch Q ersetzt, der hat die Gestalt Q mal Q max mal, und jetzt kommt es, ein Faktor, der noch zu diskutieren ist: e hoch minus K mal t mal Cosinus Omega Strich mal t. Dieser Faktor, der berücksichtigt unsere Energieverluste. Und dieser Energieverlust sind in unserem Fall zu notieren als R Ohmscher Widerstand durch 2 mal L. Diese Gleichung müssen wir jetzt noch in Verbindung bringen mit der Stromstärke I, die haben wir ja hier auf dieser Grafik zu sehen. Wir erinnern uns daran noch einmal, dass I von t gleich Q Punkt von t ist. Dass heißt, wir müssen diesen Term ableiten. Das Ganze ist ein bisschen kompliziert, aber wir können in erster Näherung für I von t folgenden Zusammenhang notieren: I von t ist ungefähr gleich minus, komme ich gleich noch einmal darauf, Imax mal e hoch minus, jetzt berücksichtigen wir die Verluste, durch zwei L mal t mal, und der Cosinus abgeleitet ist minus Sinus, daher das Minuszeichen. Sinus Omega Strich mal t. Wenn wir uns diese Formal mal anschauen und das mit unserer, mit dem Stromstärkezeitverlauf im gedämpften und ungedämpften Fall vergleichen, sehen wir, dass diese maximale Größe mit einem Term multipliziert wird, der von der Zeit abhängt und der unsere Verluste beschreibt. Dass heißt, wenn wir die Kurve, die entsprechende Kurve zeichnen, werden die jeweiligen Ausschläge nach oben und nach unten im Vergleich zur, unter Berücksichtigung der e-Funktion kleiner. Das heißt, wir haben einen Verlauf mit abnehmender Amplitude. Was ist das? Das ist eben eine gedämpfte Schwingung. Wir können die maximalen, minimal noch entsprechend miteinander durch eine Linie verbinden und diese Linie entspricht dann dieser e-Funktion. Was haben wir erreicht? Wir haben eine gute mathematische Beschreibung der gedämpften Schwingung. Aber wir haben noch eine Kleinigkeit, die wir dazu notieren können. Nämlich, wir wollen einmal vergleichen wie Kreisfrequenz und Frequenz von gedämpften und ungedämpften Fall aussehen. Hier haben wir die Kreisfrequenz der gedämpften Schwingung und diese ist gleich Wurzel 1 durch LC minus R Quadrat durch 4 L Quadrat. Ich sage gleich noch etwas dazu. Wir können uns noch die Formel für die Frequenz notieren. Die ist 1 durch 2 Pi Wurzel 1 durch LC minus R Quadrat durch 4 L Quadrat. Wenn wir die beiden Formeln jeweils miteinander vergleichen, sehen wir, dass die Formel, wenn wir dieses Glied, das die Energieverluste beschreibt in Folge der Ohmschen Widerstände vernachlässigen, dann erhalten wir sofort wieder die Formel der Kreisfrequenz für den ungedämpften Fall. Analog für die Frequenz F wenn auch hier wieder R verschwindet, steht wieder dieselbe Formel da. Wir haben damit die mathematische Behandlung der gedämpften Schwingung abgehakt. Das war es, ich hoffe, du hast alles verstanden. Vielleicht sehen wir uns wieder bei einem der nächsten Videos von Dr. Psi. Tschüss.
Mathematische Beschreibung gedämpfter elektromagnetischer Schwingungen Übung
-
Gib an, inwiefern sich eine gedämpfte und ungedämpfte Schwingung unterscheiden.
TippsStromdurchflossene Kabel erwärmen sich.
Im Schwingkreis wird Energie zwischen magnetischer und elektrischer hin- und her transferiert.
LösungDer wesentliche Unterschied zwischen ungedämpfter Schwingung und gedämpfter Schwingung lässt sich anhand der Energie gut erklären.
Die elektrische Energie, die einem Schwingkreis zugeführt wird, wird stets zwischen magnetischer und elektrischer Energie transferiert. Bei dieser Umwandlung treten nun Verluste auf, die allerdings nur bei der gedämpften Schwingung berücksichtigt werden.
Zur Vereinfachung ist die ungedämpfte Schwingung dennoch ein geeigneter Ansatz.
Die oben genannten Verluste treten in erster Linie infolge der Erwärmung der Schaltung auf. Wird ein Leiter von einem Strom durchflossen, so wird sich dieser erwärmen. Diese Wärme wird abgestrahlt und steht der Energie des Schaltkreises nicht weiter zur Verfügung. Dabei gilt, je größer der ohm'sche Widerstand ist, desto größer sind auch die Verluste.
-
Bezeichne die Bauteile im Schwingkreis.
TippsBei einer ungedämpften Schwingung wird der ohm'sche Widerstand nicht berücksichtigt.
Indem ein Kondensator geladen wird, wird dem Schwingkreis Energie hinzugefügt.
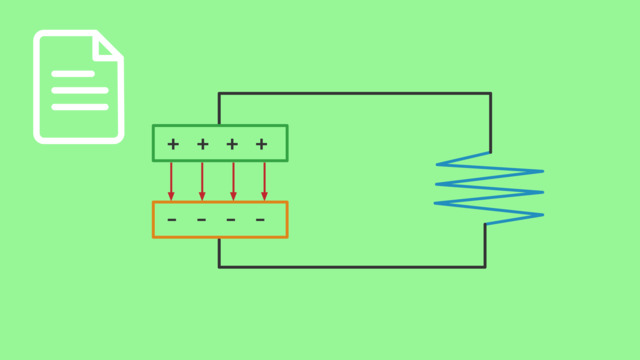
LösungIm Wesentlichen besteht der elektrische Schwingkreis aus vier Bauteilen:
Einer Spannungsquelle, einem Kondensator, einer Spule und einem Schalter zur Regelung. Dazu kommen ein Voltmeter, sowie ein Amperemeter, um die stromtechnischen Größen zu erfassen.
Mit der Spannungsquelle $U$ kann das System mit Energie geladen werden. Dazu wird die Spannungsquelle mit dem Kondensator verbunden (mittels Schalter). Infolge der Spannung bildet sich ein elektrisches Feld, welches Energie speichert.
Nun kann der Schalter umgelegt werden und der Kondensator wird von der Spannungsquelle getrennt und mit der Spule verbunden. Da nun kein äußeres Potential anliegt, muss sich der Kondensator entladen. Es fließt nun ein Strom im Stormkreis $2$, sodass die Spule stromdurchflossen ist. So muss hier ein magnetisches Feld entstehen, welches die Energie des Systems speichert.
Baut sich das Magnetfeld ab, so wird wieder eine Spannung am Kondensator induziert, wodurch dieser geladen wird.
Die Beträge der Spannung und des Stromes können mittels der Messinstrumente Amperemeter und Voltmeter jederzeit erfasst werden.
-
Zeige die Eigenschaften der gedämpften und ungedämpften Schwingung.
TippsUnterscheide nach den Verlusten.
Der Ohm'sche Widerstand spielt eine wichtige Rolle bei der Berechnung der Verluste.
LösungDer wesentliche Unterschied zwischen der gedämpften und ungedämpften Schwingung besteht im Energieverlust, der infolge der Erwärmung der Kabel nur bei der gedämpften Schwingung berücksichtigt wird.
Die ungedämpfte Schwingung im elektromagnetischen Schwingkreis zeichnet sich dadurch aus, dass dieser Energie perfekt konserviert. Das bedeutet: Wird der Schwingkreis einmal aufgeladen, so wird die Energie stets zwischen elektrischer und magnetischer Energie hin- und her transferiert.
In der Realität weisen jedoch die Kabel, welche die Bauteile des Schwingkreises miteinander verbinden, einen ohm'schen Widerstand $R$ auf, sodass Verluste entstehen. Diese werden bei der Berechnung der Frequenz und Periodendauer sowie bei Bestimmung der Kreisfrequenz berücksichtigt. Es gilt $ f' = \frac{1}{2 \pi} \cdot \sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$. Mit dem Zusammenhang $ f = \frac{1}{T} $ können wir auch die Periodendauer leicht daraus ableiten.
Wie du siehst, wird für den Fall $ R =0$ die Formel zu $ f = \frac{1}{2 \pi} \cdot \sqrt{\frac{1}{LC}}$ vereinfacht. Diese Formel wird also genutzt um die Frequenz der ungedämpften Schwingung zu bestimmen.
-
Berechne die physikalischen Größen im ungedämpften Schwingkreis.
Tipps$ E_{ges} = E_{el} + E{mgn} = const.$
Die Frequenz entspricht dem Kehrwert der Umlaufdauer.
LösungDer ungedämpfte Schwingkreis ist ein Modell eines elektromagnetischen Schwingkreises, bei dem angenommen wird, dass keine Energie verloren geht. Dabei liegt die Energie immer in Form elektrischer Energie (im Kondensator) oder aber als magnetische Energie (in der Spule) vor.
So ergibt sich $ E_{ges} = E_{el} + E{mgn} = const.$ zur mathematischen Beschreibung.
Wird diesem Kreis also einmal eine Energie zugeführt, etwa indem der Kondensator geladen wird, wird diese zwar umgewandelt, jedoch ideal konserviert und ohne Verluste gespeichert.
Thermische Verluste, wie sie bei einer elektrischen Schaltung zu erwarten sind, werden hier nicht berücksichtigt. So spielt auch der ohm'sche Widerstand der Kabel keine Rolle bei der Bestimmung der Frequenz, Kreisfrequenz oder Umlaufdauer der Schwingung.
Diese physikalischen Größen sind allein von den elektrotechnischen Eigenschaften der Bauteile Kondensator und Spule, genauer deren Kapazität $C$ und Induktivität $L$ abhängig.
Für die Periodendauer gilt $ T = 2 \pi \sqrt{LC} $. Diese steigt also mit der Kapazität des Kondensators und der Kapazität der Spule. Die Frequenz ist definiert als Kehrwert der Periodendauer, also $f = \frac{1}{T}$. Die Einheit der Frequenz ist Hertz.
Um die Kreisfrequenz zu bestimmen, verwenden wir die Formel $\omega = \frac{1}{\sqrt{LC}}$
-
Beschreibe den Ablauf im Schwingkreis.
TippsDu kannst hier von einer ungedämpften Schwingung ausgehen.
Wird ein Kondensator entladen, so fließt ein Strom.
Ist eine Spule stromdurchflossen, so entsteht ein Magnetfeld.
LösungDie Energieumwandlung im Schwingkreis läuft im Wesentlichen in vier Schritten ab.
Zunächst wird der Kondensator geladen. Die Energie wird dem System also in Form potentieller Energie im elektrischen Feld zugeführt.
Im zweiten Schritt wird der Kondensator entladen, sodass ein Strom vom Kondensator hin zur Spule fließt.
Nun wird die Spule also von einem Strom durchflossen, sodass ein Magnetfeld entstehen muss (Rechte-Hand-Regel). Zu diesem Zeitpunkt liegt die Systemenergie also als magnetische Energie vor.
Bricht das Magnetfeld in Schritt vier wieder zusammen, so fließt erneut ein Strom. Dieser lädt den Kondensator nun wieder und es herrschen exakt (bei der ungedämpften Schwingung) die gleichen Bedingungen, wie im Zustand eins.
Diese Schritte laufen periodisch immer weiter so ab, sodass eine harmonische Schwingung für den ungedämpften Schwingkreis entsteht. Handelt es sich um eine gedämpfte Schwingung, verringert sich der Energiebetrag im Zuge jeder einzelnen Schwingung. Es geht hier also Energie verloren.
-
Berechne die physikalischen Größen im gedämpften Schwingkreis.
TippsVerluste infolge des ohm'schen Widerstandes der Schaltung müssen bei der mathematischen Modellierung der gedämpften Schaltung erfasst werden.
$f = \frac{1}{2 \pi} \cdot \sqrt{ \frac{1}{LC} - \frac{R^2}{4L^2}}$
LösungIm Unterschied zu einer ungedämpften Schwingung muss der ohm'sche Widerstand der Schaltung berücksichtigt werden, um so die Verluste zu erfassen.
Neben den Eigenschaften des Kondensators und der Spule, sind also auch die der Kabel $\Omega$ von Bedeutung. Generell gilt: Je höher der ohm'sche Widerstand ist, desto größer sind die Energieverluste über die Zeit.
Diese Verluste müssen sowohl bei der Berechnung der Frequenz $f'$ als auch bei der Bestimmung von Kreisfrequenz$\omega$, Spannung $U$, Stromstärke $I$ und Energie $E_{ges}$ berücksichtigt werden.
Diese Umstände müssen auch bei der Berechnung der Periodendauer, Frequenz und Kreisfrequenz bestimmt werden.
Betrachten wir ein Beispiel: Gegeben sind $L = 0,025 H$, $C = 3,1 \cdot 10^{-8} F$ und $R = 10 \Omega$. Für die Berechnung der Frequenz gilt die gezeigte Formel. Setzen wir nun ein, so ergibt sich: $ f = \frac{1}{2 \pi} \cdot \sqrt{ \frac{1}{0,025 H \cdot 3,1 \cdot 10^{-8} F} - \frac{(10 \Omega)^2}{4 \cdot (0,025 H)^2}} = 5716,92 Hz$.
Die Frequenz der der Schwingung beträgt also etwa $f = 5717 Hz$.
9.178
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.108
Lernvideos
37.100
Übungen
33.418
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?














Hatte einen Denkfehler. Sorry
Beim Vergleich zum Schluss. kommt mir etwas sehr komisch vor. Wenn der Ohmsche Wirderstand R null wird, dann ist die Gleichung zwar ähnlich zur ungedämpften Gleichung, aber es sind doch nicht die selben. Also entweder ich habe einen Denkfehler oder es wird hier falsch dargestellt.