Zyklotron – Überblick
Ein Zyklotron ist ein Teilchenbeschleuniger, der geladene Teilchen mithilfe eines Magnetfelds auf eine spiralförmige Bahn beschleunigt. Erfahre, wie sich die Kreisfrequenz der Teilchen mit der Wechselspannung abstimmt und wie das Zyklotron in Experimenten eingesetzt wird. Interessiert? Dies und mehr findest du im folgenden Text!

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Zyklotron – Überblick
Was ist ein Zyklotron?
Das Zyklotron ist ein Teilchenbeschleuniger, in dem geladene Teilchen durch ein elektrisches Wechselfeld schubweise beschleunigt werden. Dabei werden sie von einem senkrecht zu ihrer Bewegungsrichtung wirkenden Magnetfeld auf eine nahezu spiralförmige Bahn geführt, bis sie bei hoher Geschwindigkeit ausgekoppelt und auf ein Ziel gelenkt werden können.
Aufbau – Zyklotron

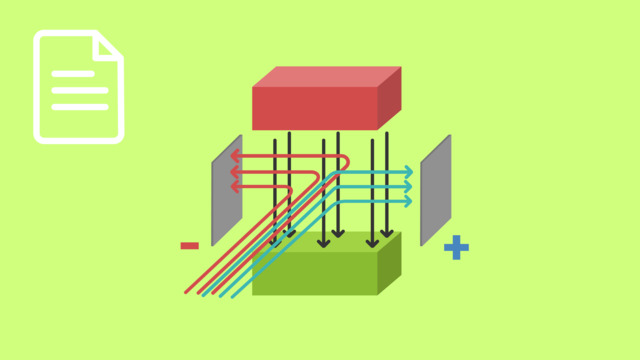
Das Zyklotron besteht aus zwei halbkreisförmigen hohlen Elektronen (Duanten), die durch einen Spalt getrennt sind. In der Mitte werden die geladenen Teilchen durch eine stecknadelgroße Quelle eingebracht. Innerhalb des Spaltes werden die geladenen Teilchen beschleunigt. Durch ein vertikal orientiertes Magnetfeld werden die geladenen Teilchen auf eine Kreisbahn gezwungen, welche durch die stete Beschleunigung zu einer Spirale wird.
Zyklotron – Funktionsweise In einem Zyklotron werden die geladenen Teilchen stark beschleunigt, dazu wird eine hochfrequente Wechselspannung verwendet. Diese sehr große Frequenz $f$ wird genutzt, um die Beschleunigungswege möglichst klein zu halten. Dies lässt sich am Linearbeschleuniger zeigen, hier werden Driftröhren eingesetzt, deren Polung genau so durch die Wechselspannung geändert wird, dass sie das geladene Teilchen anziehen und, sobald es die Röhre verlassen hat, wieder abstoßen. Durch die dadurch steigende Geschwindigkeit $v$ der Teilchen müssen diese Röhren immer länger werden.
Die Länge $l$ der Röhren lässt sich berechnen mit:
$l=v\cdot \dfrac{T}{2}=v\cdot \dfrac{1}{2f}$
Durch die immer längeren Röhren wird dafür gesorgt, dass die Teilchen mit ihrer steigenden Geschwindigkeit mit der Wechselfrequenz der Beschleunigungsspannung im Takt bleiben.
Das Zyklotron ist deutlich kompakter gebaut als der Linearbeschleuniger, da es die Teilchen auf eine Spiralbahn zwingt. Und wer schon einmal eine Lakritzschnecke abgerollt hat, erkennt, dass diese Bauweise deutlich kompakter ist.
Das Zyklotron nutzt dafür aus, dass geladene Teilchen durch die Lorentzkraft in einem Magnetfeld abgelenkt werden. Steht das Magnetfeld genau senkrecht zur Bewegungsrichtung, wird das Teilchen auf eine Kreisbahn abgelenkt.

Für eine Kreisbahn gilt, dass die Lorentzkraft $F_L$ und die Zentripetalkraft $F_Z$ gleich groß sein müssen:
$F_Z=F_L \longrightarrow \frac{m\cdot v^2}{r}=q \cdot v \cdot B$
Daraus folgt für die Geschwindigkeit $v$:
$v=\frac{r \cdot q \cdot B}{m}$
Das Teilchen rotiert dabei mit der Kreisfrequenz $\omega$ auf der Kreisbahn:
$\omega=\frac{v}{r}=\frac{q \cdot m}{B}$
Dabei steht:
- $m$ für die Teilchenmasse in $\text{kg}$,
- $q$ für die Teilchenladung in $\text{C}$,
- $B$ für die magnetische Flussdichte in $\text{T}$,
- $v$ für die momentane Teilchengeschwindigkeit in $\frac{\text{m}}{\text{s}}$,
- $r$ für den Bahnradius in $\text{m}$ und
- $\omega$ für die Kreisfrequenz in $\text{Hz}$.
Damit das Teilchen im Zyklotron immer dann beschleunigt wird, wenn es sich im Spalt befindet, muss die Frequenz $f$ der Wechselspannung so gewählt werden, dass sie mit der Kreisfrequenz $\omega$ im Takt ist, dadurch ändert sich die Polung der Elektroden wie beim Linearbeschleuniger immer gerade so, dass das Teilchen von der Elektrode in Flugbahn angezogen wird und von der Elektrode hinter sich abgestoßen wird:
$f = \frac{\omega}{2\pi}$
Durch die immer höhere Geschwindigkeit des Teilchens muss der Bahnradius der Kreisbahn auch immer größer werden, da die Kreisfrequenz bei der Beschleunigung konstant bleibt. Dadurch wird das Teilchen auf eine Spiralbahn gezwungen.
$\omega=\frac{v}{r}=2 \pi \cdot f$
$r(v)=\frac{v}{\omega}\quad |\omega = \text{konst.}$
Am Ende der Spirale wird das Teilchen durch ein weiteres Magnetfeld auf eine geradlinige Bahn gezwungen und verlässt das Zyklotron mit seiner Endgeschwindigkeit.
Zyklotron Beispiel
In einem Zyklotron wird zum Testen ein Proton beschleunigt. Das Zyklotron besitzt einen Durchmesser von $d=16 \text{ m}$. Die Teilchenmasse des Protons
Gegeben:
$d=16 \text{ m}$
$~m_\text{Proton}=1,6726 ⋅ 10^{−24} \text{kg}$
$Q_\text{Proton}=+1,602 ⋅ 10^{−19} \text{ C}$
$~B=2\text{ T}$
Gesucht:
$~v_\text{End}$
Die Beschleunigungsfrequenz $f$ wird der Kreisfrequenz $\omega$ des Teilchens angepasst.
$\begin{aligned}f &= \dfrac{Q \cdot B}{2\pi\cdot m}\\ &=\dfrac{1,602 \cdot 10^{−19}\text{ C}\cdot 2\text{ T}}{2\pi\cdot 1,6726 ⋅ 10^{−24} \text{ kg}}\\ &\approx 30\,487 \text{ Hz} \end{aligned}$
Die Kreisfrequenz $\omega$ ist dann gleich:
$\omega=2\pi \cdot f= 2\pi \cdot 30\,487 \text{ Hz}=191\,561 \text{Hz}$
Stellen wir
$\omega=\frac{v}{r}$
nach $v$ um, können wir mit dem bekannten Radius des Zyklotrons die Endgeschwindigkeit bestimmen.
$\begin{aligned} v&=\omega \cdot r\\ &= 95\,779 \text{Hz} \cdot 8 \text{m}\\ &=1\,532\,494 \frac{\text{m}}{\text{s}}\\ &=0,0051c \end{aligned}$
Zyklotron Anwendung
Das Zyklotron ist ein Teilchenbeschleuniger für geladene Teilchen. Die beschleunigten Teilchen werden dann für viele physikalische Experimente genutzt. Sei dies ein Kollisionsexperiment, bei dem man das Teilchen mit anderen Teilchen kollidieren lässt oder die Erzeugung neuer Elemente. Einige Elementarteilchen wurden bereits mit dem Zyklotron entdeckt. Durch die großen Teilchenbeschleuniger, welche eine noch größere Beschleunigung der Teilchen ermöglichen, konnten aber noch weit mehr Elementarteilchen entdeckt werden.
Grenzen des Zyklotrons
Durch die relativistische Massenzunahme der Teilchen kann mit einem normalen Zyklotron das Teilchen nur auf eine Geschwindigkeit von etwa $0,1c$ beschleunigt werden. Durch die Massenzunahme ändert sich die Kreisfrequenz $\omega$ des Teilchens und passt dann nicht mehr zur Beschleunigungsfrequenz $f$ der Wechselspannung. Höhere Geschwindigkeiten sind mit einem Syncro-Zyklotron möglich, hier wird die Wechselfrequenz des Beschleunigungsfeldes stetig der Teilchenmasse angepasst.
Transkript Zyklotron – Überblick
Hallo und herzlich willkommen. Ich zeige hier, wie ein Zyklotron aufgebaut ist, und erkläre sein Funktionsprinzip. Du solltest das Verhalten bewegter Ladungsträger in elektrischen und magnetischen Feldern kennen und insbesondere die Wirkung der Lorenzkraft. Stellen wir uns eine flache runde Keksdose vor, die nahezu luftleer gepumpt ist und in ihrem inneren einer weitere flache runde Dose enthält. Diese innere Dose ist in der Mitte längs durchgeschnitten, sodass sich zwei halbierte Dosen mit einem schmalen Spalt gegenüberstehen. Im Mittelpunkt der äußeren Dose, also genau im Spalt der Inneren, steht so etwas wie eine kleine Stecknadel mit einem Kanal, der in ein Loch im Kopf der Stecknadel mündet. Durch diesen Kanal können wir geladene Teilchen in die Dose hineinträufeln. Legen wir eine Spannung zwischen die Hälften der inneren Dose, baut sich am Spalt ein elektrisches Feld auf, dass unser geladenes Teilchen in Richtung einer der Dosenhälften lenken wird. Dann setzen wir diese Anordnung noch in ein konstantes magnetisches Feld. So, dass das magnetische Feld senkrecht auf den Grundflächen steht. Dann wird ein jedes der geladenen Teilchen, die wir in der Mitte der Dose ins Innere träufeln zwar vom elektrischen Feld zur Seite in Bewegung gesetzt, aber zugleich durch das Magnetfeld zur Seite abgelenkt, weil die Lorenzkraft wirkt. Weil das Teilchen in einer Ebene fliegt, die den Grundflächen unserer Dose genau parallel liegt, bleibt seine Bewegung trotz der Richtungsänderung weiterhin genau rechtwinklig zur Ausbreitung des magnetischen Feldes. Das heißt aber, dass die Lorenzkraft auf allen Punkten seiner Bahn mit unverminderter Stärke immer rechtwinklig zur Bewegungsrichtung wirkt. Wenn aber die Bahngeschwindigkeit des Teilchens, wie hier, unverändert bleibt, bedeutet eine konstante Kraft zur Seite hin eine gleiche Abweichung zur Seite in jedem Punkt der Bahn. Also ist die Bahn an allen Punkten gleich stark gekrümmt. Es gibt nur eine geometrische Figur in der Ebene, die eine Linie mit überall gleicher Krümmung besitzt. Das ist der Kreis. Sehen wir mal von der mathematischen Spitzfindigkeit ab, dass auch eine Gerade überall gleich gekrümmt ist, nämlich gar nicht. Genauer hergeleitet findet man diesen Umstand in der Mechanik bei der Untersuchung der gleichförmigen Kreisbewegung. Für geladene Teilchen mit konstanter Bahngeschwindigkeit ergibt sich also bei Bewegung in einer Ebene, die rechtwinklig zum magnetischen Feld steht, eine Kreisbewegung. Aber dafür ist das Zyklotron nicht konstruiert worden. Hier wird nämlich eine Wechselspannung an die geteilte innere Dose angelegt und genau so justiert, dass sich das elektrische Feld genau dann umpolt, wenn das Teilchen auf dem äußersten Punkt seiner Bahn läuft und sich eben wieder in Richtung auf den Spalt zu bewegt. Folgt der Verlauf der Wechselspannung einer Sinusfunktion, hat das von ihr, jetzt in der entgegengesetzen Richtung aufgebaute elektrische Feld, gerade dann sein Maximum, wenn das Teilchen wieder in den Spalt hineinfliegt. Das bedeutet, dass es aber nun in seine Bewegungsrichtung eine Kraftwirkung erfährt. Es wird kurz beschleunigt und dadurch schneller. Das heißt aber nun, dass auch die Lorenzkraft größer wird. Erinnern wir uns an die gleichförmige Kreisbewegung, fällt uns ein, dass die Zentripetalkraft, die eine Kreisbewegung kennzeichnet, nach der Formel FZ=m×(v2/r) berechnet wurde. Sie muss hier in unserer Versuchsanordnung offenkundig der Lorenzkraft entsprechen, also muss gelten: Zentripetalkraft gleich Lorenzkraft. Daraus folgt die Beziehung v/r=(q×B)/m. Das heißt, wenn sich die Bahngeschwindigkeit des Teilchens erhöht, muss sich auch der Radius des Kreises, auf dem es umläuft, vergrößern, solange die Ladung q, die Masse m des Teilchens und die magnetische Flussdichte B konstant bleiben. Der Ausdruck v/r ist natürlich gleich der Winkelgeschwindigkeit Omega, die also hier konstant bleibt, solange Ladung, Masse und Flussdichte B konstant bleiben. Dann leuchtet vielleicht sofort ein, dass wir mit einer sinusförmigen Wechselspannung der Frequenz f ein perfekt abgestimmtes System haben, in dem das kreisende Elektron immer genau dann einen zusätzlichen Stoß in Bewegungsrichtung erfährt, wenn es den Spalt passiert. Weil es dadurch schneller wird, muss der Radius seiner Kreisbahn größer werden und es ergibt sich eine spiralförmige Bahn, auf der wir das Teilchen schneller und schneller werden sehen. Im Zyklotron wird es schließlich auf einer weit außen liegenden Bahn von einem elektrischen Feld abgelenkt, aus dem Zyklus befreit und mit seiner hohen Geschwindigkeit auf ein Ziel, ein sogenanntes target gelenkt. Zusammenstöße der beschleunigten Elektronen mit Atomen oder auch freien Elektronen des ... Materials erzeugen Effekte, die man dann sorgfältig untersuchen kann. Weil die Winkelgeschwindigkeit Omega, wie vorhin notiert, unter anderem von der Masse des Teilchens abhängt, muss man sie nachjustieren, wenn das Teilchen während seines Fluges schwerer werden sollte. Und genau das geschieht ja, wenn es so schnell wird, dass der relativistische Effekt der Massenzunahme bemerkbar wird. Für bestimmte Zwecke, für die man hochbeschleunigte Teilchen aus dem Zyklotron erhalten will, muss man also mit der relativistischen Massenzunahme die Frequenz verkleinern, um die Beschleunigungsschübe mit der Spiralbewegung synchron zu halten. Das Gerät, mit dem man das kann, nennt man Synchrozyklotron. Kurz und prägnant zusammengefasst ist ein Zyklotron also ein Gerät, in dem geladene Teilchen durch ein elektrisches Wechselfeld schubweise beschleunigt werden und dabei von einem Magnetfeld senkrecht zu ihrer Bewegungsrichtung auf einer nahezu spiralförmigen Bahn geführt werden, bis sie bei hoher Geschwindigkeit ausgekoppelt und auf ein Ziel gelenkt werden können. So viel für dieses Mal. Bis zum nächsten Video!
Zyklotron – Überblick Übung
-
Bezeichne den Aufbau des Zyklotrons.
TippsIm Zyklotron wirkt die Lorentzkraft.
Nur geladene Teilchen können im Zyklotron beschleunigt werden.
LösungDas Zyklotron besteht aus mehreren einzelnen Bauteilen.
Eine Ionenquelle befindet sich zwischen den beiden Duanten. Diese Anordnung ist von einem Gehäuse umgeben.
Darüber hinaus liegt ein Magnetfeld an. Damit sind die Wesentlichen Bauteile des Zyklotrons schon beschrieben.
Wird nun ein geladenes Teilchen aus der Ionenquelle emittiert, so ist dieses dem Einfluss der Duanten und des Magnetfeldes ausgesetzt.
Zwischen den Duanten wirkt ein elektrisches Feld, welches das Ion beschleunigt. Diese Bewegung des Teilchens können wir als einen Strom verstehen. Ein Strom ist ja $ I = \frac{Q}{t} $, also Ladung pro Zeit.
Liegen ein Strom und ein Magnetfeld vor, die senkrecht aufeinander stehen, dann muss die Lorentzkraft wirken.
Diese lenkt das Ion auf die charakteristische Kreisbahn.
Hat das beschleunigte Teilchen nun seine vorgesehene Geschwindigkeit erreicht, verlässt es die Kreisbewegung im Zyklotron und wird mithilfe eines elektrischen Feldes auf ein Target, also ein Ziel, gelenkt.
Genutzt wird das Zyklotron in der Medizin, für bestimmte Strahlentherapien oder in der physikalischen Forschung.
-
Erkläre, wie die spiralförmige Bahn des Teilchens im Zyklotron entsteht.
TippsDas Zyklotron ist ein Gerät, welches man benutzt, um Teilchen zu beschleunigen.
Die Beschleunigung erfolgt in Schüben.
LösungDie Ionenquelle im Zentrum des Zyklotrons sendet geladene Teilchen aus.
Diese sind direkt dem elektrischen Feld ausgesetzt, welches zwischen den Duanten herrscht. Weiterhin wirkt ein magnetisches Feld auf die Teilchen.
Die beiden Felder führen dabei unterschiedliche Funktionen aus.
Das elektrische Feld bewirkt die Beschleunigung des Teilchens. Immer wenn der Spalt zwischen den Duanten überschritten wird, wird dieses beschleunigt. Man sagt, es handelt sich um eine schubweise Beschleunigung.
Damit sich das Teilchen nun in einer Spiralform bewegt, muss es einen Einfluss geben, der bewirkt, dass die geradlinige, schubweise Beschleunigung durch das elektrische Feld gelenkt wird.
Dafür benutzt man das magnetische Feld. Da hier nun ein Strom (bewegtes geladenes Teilchen) senkrecht zum Magnetfeld fließt, muss die Lorentzkraft auftreten. Diese ist im Zyklotron immer so gerichtet, dass diese zum Zentrum hin gerichtet ist.
Durch wiederholtes Beschleunigen des Teilchens, wird dessen Geschwindigkeit größer.
Dadurch kann die Lorentzkraft die Bewegung nicht weiter auf einer engen Kreisbahn halten und der Kreis wird immer größer, also zur Spirale.
Du kannst diesen Effekt gut nachvollziehen, wenn du eine Münze an einem Gummiband befestigst und dieses dann wie ein Lasso schwingst. Je schneller die Drehung des Gummibandes, desto größer ist die Bahn, die die Münze beschreibt.
Im Zyklotron wird, sobald eine weit außen liegende Bahn erreicht ist, das Teilchen durch ein elektrisches Feld geradlinig herausgeschossen und auf ein Zielobjekt gelenkt.
-
Zeige die Zusammenhänge.
TippsEin Ion ist ein geladenes Teilchen.
Ein geladenes Teilchen wird im elektrischen Feld beschleunigt.
Fließt ein Strom senkrecht zu einem Magnetfeld, tritt die Lorentzkraft auf.
LösungUm zu erklären, wie ein Ion im Zyklotron beschleunigt wird, müssen wir im Wesentlichen betrachten, wie sich Magnetfeld und elektrisches Feld auf die Bewegung des Teilchens auswirken.
Ein geladenes Teilchen trägt immer eine bestimmte Ladung. Betrachten wir hier ein Elektron. Dieses ist negativ geladen und wird in einem elektrischen Feld also auf den $+$Pol hin beschleunigt.
Im Zyklotron befindet sich das elektrische Feld zwischen den flachen Seiten der beiden Duanten.
Da sich durch das Anlegen einer Wechselspannung die Richtung des elektrischen Feldes immer wieder ändert, wird das Elektron bei jedem Durchlauf des Feldes beschleunigt und nicht ausgebremst.
Das elektrische Feld ist also für die Beschleunigung der Teilchen verantwortlich.
Damit das bewegte Teilchen nun nicht direkt an das Gehäuse stößt, muss es auf eine Kreisbahn gelenkt werden. Das geschieht, durch das Magnetfeld.
Genauer gesagt wirkt die Lorentzkraft, als Resultat aus elektrischem Strom und dazu senkrechtem Magnetfeld auf das Teilchen und lenkt dieses ab.
Dabei kann das Teilchen umso mehr abgelenkt, der Radius des Kreises, den es beschreibt also umso größer sein, je geringer die Geschwindigkeit des Teilchens ist.
Wie bereits beschrieben, wird das Teilchen jedoch immer schneller. Als Folge davon muss also auch der Radius der Teilchenbahn immer größer werden, sodass eine spiralförmige Bewegung entsteht.
-
Berechne die Frequenzen der Wechselspannungen.
TippsDer Betrag der Ladung ist $q$ stets $q_{el} = q_{prot} = 1e$
$ f = \frac{q \cdot B }{2 \cdot \pi \cdot m}$
LösungDamit ein Teilchen im Zyklotron immer weiter beschleunigt werden kann, muss immer zum richtigen Zeitpunkt der angelegte Strom in die passende Richtung fließen.
Erinnere dich an die Linke-Hand-Regel ,die Richtung der Lorentzkraft hängt von der Richtung des Magnetfeldes und der Stromrichtung ab.
Im Zyklotron ist das Magnetfeld konstant, die Stromrichtung und damit die Richtung der Lorentzkraft ändern sich jedoch immer wieder.
Nun wird ein Ion jedesmal beschleunigt, wenn es den Spalt zwischen den Duanten passiert. Wie häufig der Spalt passiert wird, ist natürlich abhängig von der Geschwindigkeit des Teilchens, genauer der Winkelgeschwindigkeit. Den Ansatz $ \omega = 2 \cdot \pi \cdot f$ lösen wir nach $f$ auf und erhalten $ f = \frac{\omega}{2\cdot\pi}$.
Die Geschwindigkeit $\omega$ lässt sich auch durch die Ladung und Masse des Teilchens und das Magnetfeld ausdrücken:
$ \omega = \frac{q \cdot B}{m}$
Abhängig von der Masse des Teilchens $m$ und seiner Ladung $q$ muss also, in einem Magnetfeld $B$, eine bestimmte Frequenz $f$ angelegt werden.
Wir erhalten die Formel $ f = \frac{q \cdot B }{2 \cdot \pi \cdot m}$.
Dabei ist der Betrag der Ladung $q$ stets $q_{el} = q_{prot} = 1e$, also eine Elementarladung.
Betrachten wir ein Beispiel:
Ein Elektron mit $m_{el} = 9,1 \cdot 10^{-31} kg$ und $ q = 1,6 \cdot 10^{-19} C$ wird in einem Zyklotron mit dem Magnetfeld $ B = 580 mT$ eingebracht.
Zunächst müssen wir umformen: $ 580 mT = 0,58T$.
Wir setzen nun in $ f = \frac{q \cdot B }{2 \cdot \pi \cdot m}$ ein und erhalten $f = \frac{ 1,6 \cdot 10^{-19} C \cdot 0,58T }{2 \cdot \pi \cdot 9,1 \cdot 10^{-31} kg} = 16,23 GHz$.
-
Nenne die richtigen Aussagen über das Zyklotron.
TippsIonen sind stets geladene Teilchen.
Teilchen werden nur zwischen den Duanten beschleunigt.
LösungIm Inneren des Zyklotrons befindet sich immer eine Ionenquelle, die zwischen zwei Duanten angebracht ist.
An den Duanten ist eine Wechselspannung abgebracht, sodass zwischen diesen ein elektrisches Feld herrscht, welches seine Richtung immer wieder wechselt.
Die Ionenquelle sendet nun geladene Teilchen aus, die von dem elektrischen Feld beschleunigt werden. Ein Neutron würde unbeeinflusst vom elektrischen Feld bleiben und somit nicht beschleunigt.
Damit die beschleunigten Ionen auf einer spiralen Bahn um die Ionenquelle verlaufen, muss ein Magnetfeld senkrecht zur flachen Seite der Duanten herrschen.
Ist dies der Fall, wirkt die Lorentzkraft auf die bewegten, geladenen Teilchen und diese werden auf den Mittelpunkt ihrer Kreisbewegung hingelenkt.
Da ein Teilchen sehr häufig durch das elektrische Feld zwischen den Duanten laufen kann und damit immer weiter beschleunigt wird, können relativistisch relevante Geschwindigkeiten erreicht werden.
-
Analysiere den Einfluss der relativistischen Masse.
TippsLösungDa in einem Zyklotron sehr hohe Geschwindigkeiten erreicht werden können, müssen wir betrachten, was passiert, wenn $v > \frac {1}{10} c $ und damit eine relativistisch relevante Geschwindigkeit erreicht ist.
Dazu müssen wir die relativistische Masse berücksichtigen. Diese errechnet sich aus $ m_{rel} = m_ 0 \cdot \frac {1}{\sqrt{1- \frac{v^2}{c^2}}}$.
Die Masse steigt also mit der Geschwindigkeit an.
Integrieren wir $m_{rel}$ in die Formel zur Berechnung der Wechselfrequenz, so ergibt sich:
$ f = q \cdot B \cdot \frac{1}{2 \cdot \pi m_{rel}}$ $ = \frac{q \cdot B \cdot \sqrt{1- \frac{v^2}{c^2}}}{2 \cdot \pi \cdot {m_0}}$
Damit muss also eine geringere Frequenz angelegt werden, je weiter ein Teilchen die Grenze von $ v = \frac{1}{10} c $ überschreitet.
Das ist deshalb wichtig, da die Wechselfrequenz festlegt, zu welchem Zeitpunkt und in welcher Richtung das elektrische Feld vorliegt.
Durchliefe das beschleunigte Teilchen das elektrische Feld zu einem falschen Zeitpunkt, würde dieses gebremst und das Zyklotron würde nicht mehr seinem Zweck gerecht.
Mithilfe der Beobachtungen von Albert Einstein, können wir dieses Problem jedoch leicht lösen und das Zyklotron kann auch bei Geschwindigkeiten $ v > \frac{1}{10} c $ funktionieren.
9.178
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.108
Lernvideos
37.100
Übungen
33.418
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?