Thermodynamische Prozesse
Thermodynamische (Kreis)-Prozesse werden durch Zustandsänderungen und ihren thermischen Wirkungsgrad definiert.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Einleitung
Die industrielle Revolution im 19. Jahrhundert wurde getrieben durch die Erfindung der Dampfmaschine. Eine Dampfmaschine nutzt die Wärme des Wasserdampfes, um einen Kolben anzutreiben, der dann wiederum Züge oder Maschinen antreiben kann. Die Dampfmaschine kann also allein mit Hilfe von Wärme Arbeit verrichten, was industrielle Prozesse beschleunigt und den Menschen harte Arbeit abnimmt.
Die Dampfmaschine ist im thermodynamischen Sinne ein thermodynamischer Kreisprozess. Auch heutzutage sind sie von großer Bedeutung: Jeder Dieselmotor und jeder Kühlschrank ist ein thermodynamischer Kreisprozess. Motoren wie auch die Dampfmaschine sind sogenannte Wärmekraftmaschinen, das heißt, dass sie durch Wärmeübertragung Arbeit verrichten. Ein Kühlschrank ist eine Kältemaschine oder Wärmepumpe und funktioniert im Prinzip entgegengesetzt, es wird also Arbeit verrichtet um Wärme aus dem Kühlschrank zu „pumpen“. Wie genau, kannst du im Folgenden lernen.
Thermodynamische Grundlagen und Kreisprozess
In der Thermodynamik gibt es Zustandsgrößen, die den Zustand eines thermodynamischen Systems beschreiben. Dazu gehören die Temperatur $T$, der Druck $p$ und das Volumen $V$. In thermodynamischen Kreisprozessen betrachtet man meist nur ideale Gase und daher gilt das allgemeine Gasgesetz:
$ p \cdot V = n \cdot R \cdot T $.
Das Gasgesetz beschreibt den Zusammenhang zwischen den drei Zustandsgrößen. Dabei steht $n$ für die Stoffmenge und $R$ für die universelle Gaskonstante.
Wie der Name schon suggeriert sind Kreisprozesse thermodynamische Prozesse, die periodisch ablaufen, das heißt, der Anfangspunkt eines jeden Prozesses ist auch dessen Endpunkt. Während des Kreisprozesses durchläuft das System eine Reihe von Zustandsänderungen, so kann sich beispielsweise die Temperatur oder der Druck eines Systems ändern. Nach einem Durchlauf sind aber alle Zustandsgrößen wieder so groß wie zu Beginn.
Im Gegensatz zu Zustandsgrößen können Prozessgrößen nur bei Zustandsänderungen auftreten. Prozessgrößen sind zum Beispiel die Arbeit $W$, die ein System verrichten kann, und die Wärme $Q$, die dabei aufgenommen oder abgegeben wird.
Carnot-Prozess und Wirkungsgrad
Ein Carnot-Prozess ist ein idealer und daher nicht realer thermodynamischer Kreisprozess. Alle Kreisprozesse lassen sich am einfachsten in $V$-$p$-Indikatordiagrammen darstellen. Das sind Diagrammen mit zwei Achsen: Die x-Achse bezeichnet das Volumen und die y-Achse gibt den Druck eines Systems an. Durch Punkte in diesem Koordinatensystem werden Zustände dargestellt, Zustandsänderungen durch Verbindungslinien. Ein Kreisprozess kann im Indikatordiagramm ein Kreis sein, aber auch ein Rechteck oder Vieleck mit geraden oder krummen Linien. Das Entscheidende ist, dass alle Diagramme geschlossen sind wie ein Kreis.
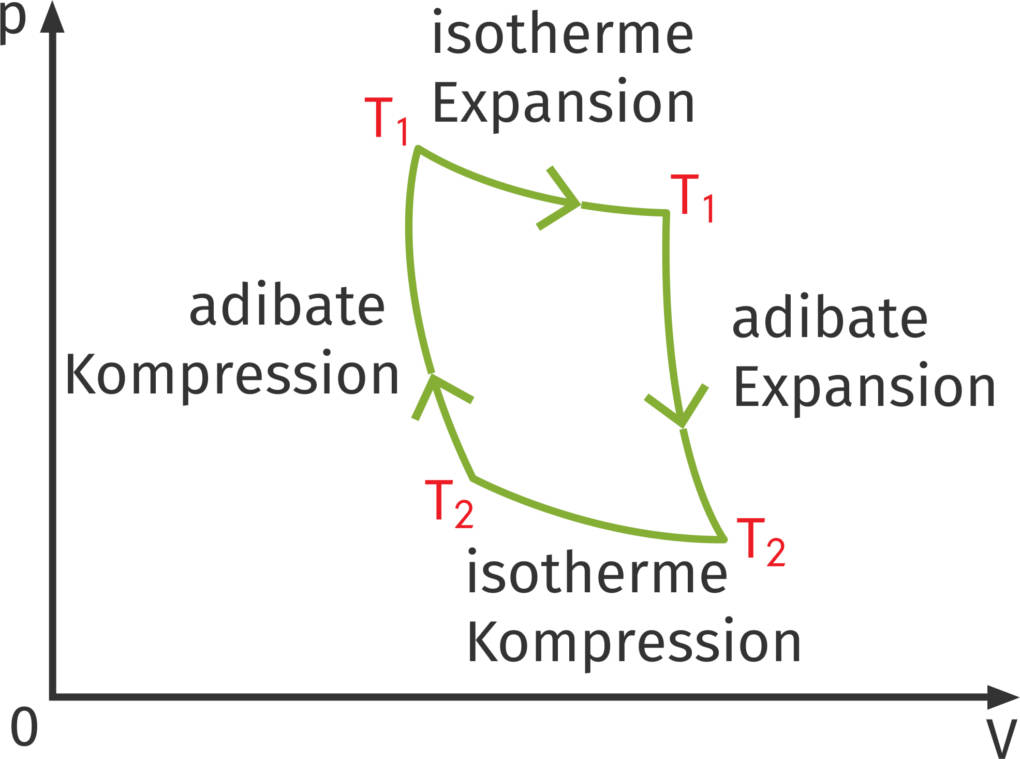
Die Fläche, die der Kreisprozess im Diagramm einschließt, ist die verrichtete Arbeit des Systems, also die Arbeit, die ein Motor leisten kann. Man kann zeigen, dass sich die Arbeit folgendermaßen berechnet:
$W_\text{gesamt}=(T_1 - T_2) \cdot R \cdot ln(\frac{V_1}{V_2})$.
Die Arbeit, die ein System leisten kann, hängt also nur von der Temperaturdifferenz und den Volumina ab. Dazu benötigt der Motor Wärme, die er durch die Verbrennung des Sprits erzeugt. Leider ist rein physikalisch nicht alle Wärme nutzbar, sodass ein Teil der Wärme wieder durch den Auspuff abgegeben wird. Daher ist die Arbeit eines Systems auch die Differenz zwischen der zugeführten und abgeführten Wärme.
Wirkungsgrad
Wie du dir vorstellen kannst, möchte man am Liebsten einen möglichst effizienten Motor bauen, damit man auch etwas von dem Sprit hat, den man teuer bezahlen muss. Ein Maß für die Effizienz eines thermodynamischen Kreisprozesses ist der thermische Wirkungsgrad $\eta$, der das Verhältnis aus verrichteter Arbeit und zugeführter Wärme ist und nur von der Temperatur abhängt.
$\eta=\frac{\text{verrichtete Arbeit}}{\text{zugeführte Wärme}}=\frac{T_1 - T_2}{T_1}<1$
Selbst der ideale Wirkungsgrad eines Kreisprozesses ist immer kleiner als 1. In der Realität treten zusätzlich Reibungsverluste auf, die den Wirkungsgrad weiter verringern.
Nachteile von Verbrennungsmotoren
Bei den meisten Verbrennungen werden Oxide frei, die sich negativ auf das Klima und auch auf deine Gesundheit auswirken. Daher wird verstärkt an Alternativen zum Verbrennungsmotor geforscht. Gerade Brennstoffzellen und Elektromotoren zeigen hier Potential. Aber auch mit Biokraftstoffen wird versucht, die Klimabilanz der Verbrennungsmotoren zu verbessern.
Zustandsänderungen
Wie oben beschrieben, ist ein Kreisprozess eine Reihe verschiedener Zustandsänderungen, während der sich mindestens eine Zustandsgröße verändert und andere konstant bleiben. Je nachdem, um welche Größen es sich handelt, folgen unterschiedliche Gesetze.
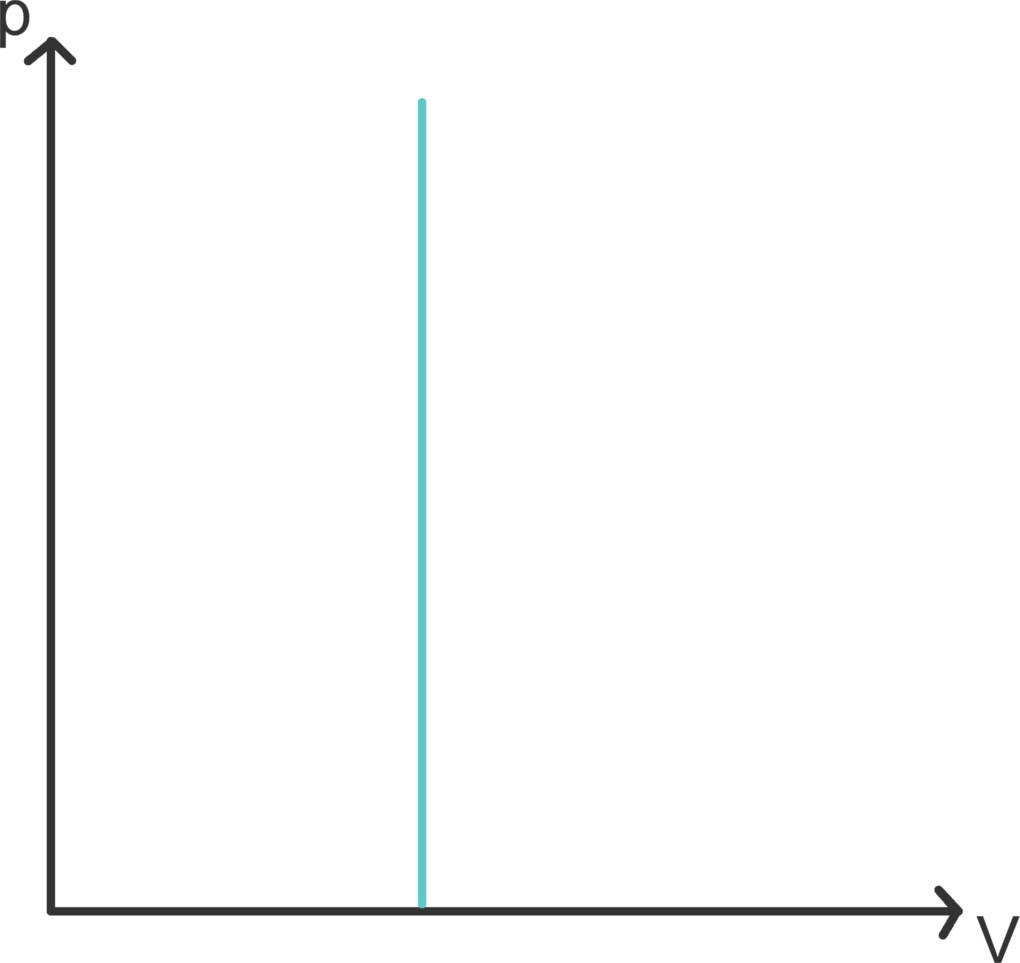
Isochore Zustandsänderungen
Isochore Zustandsänderungen bezeichnen Prozesse mit konstantem Volumen, wie sie beispielsweise in einer Thermoskanne stattfinden, die immer gleich groß ist. Füllst du heißen Kaffee in die Kanne, so herrscht zunächst Normaldruck. Wenn der Kaffee und die Luft in der Flasche sich dann abkühlen, muss nach dem Gasgesetz auch der Druck kleiner werden. Tatsächlich hörst du ein Zischen des Druckausgleichs, wenn du die Flasche wieder öffnest.
Vielleicht erinnerst du dich an den 1. Hauptsatz der Thermodynamik? Er besagt, dass die Änderung der inneren Energie eines Systems gleich der Summe aus der Änderung der Wärme und der verrichteten Arbeit am System ist.
$ \Delta E = \Delta Q + \Delta W $
Eine isochore Zustandsänderung ist im $V$-$p$-Diagramm eine Senkrechte. Da keine Volumenarbeit verrichtet wird ($\Delta W=0$) ist $\Delta E=\Delta Q$. Die innere Energie der Thermosflasche hat sich also allein durch Wärmeabgabe verringert.
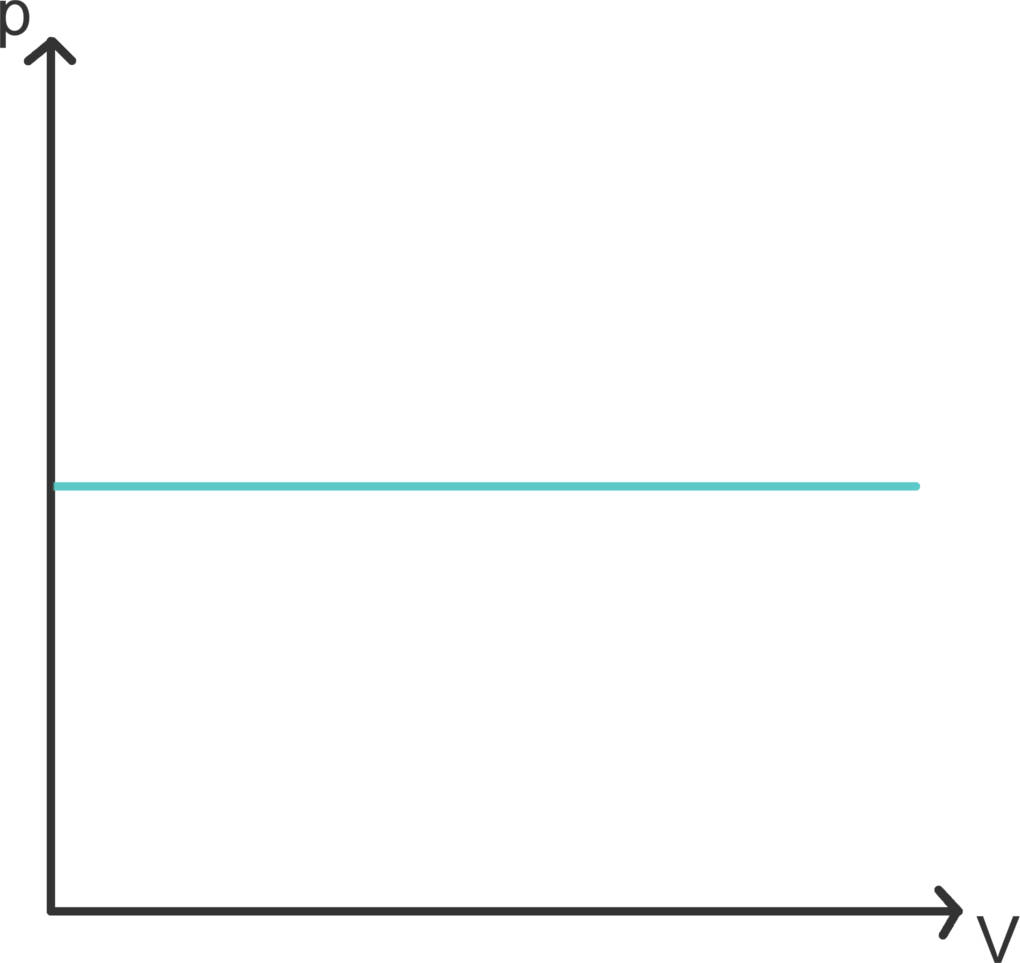
Isobare Zustandsänderungen
Eine isobare Zustandsänderung ist ein Prozess mit konstantem Druck. In einem Luftballon herrscht immer Luftdruck. Legst du ihn in die Sonne, erhöht sich seine Temperatur im Inneren. Stellst du das Gasgesetz um, so erkennst du, dass sich folglich auch das Volumen vergrößern muss. Tatsächlich bläht sich ein Ballon in der Sonne auf und schrumpft im Kühlschrank.
Im Diagramm ist eine Isochore eine Waagerechte. Die Änderung der inneren Energie (des Luftballons) ergibt sich aus zugeführter Wärme (Sonneneinstrahlung) und verrichteter Volumenarbeit (Wachsen bzw. Schrumpfen): $\Delta E = \Delta Q + p\Delta V$.
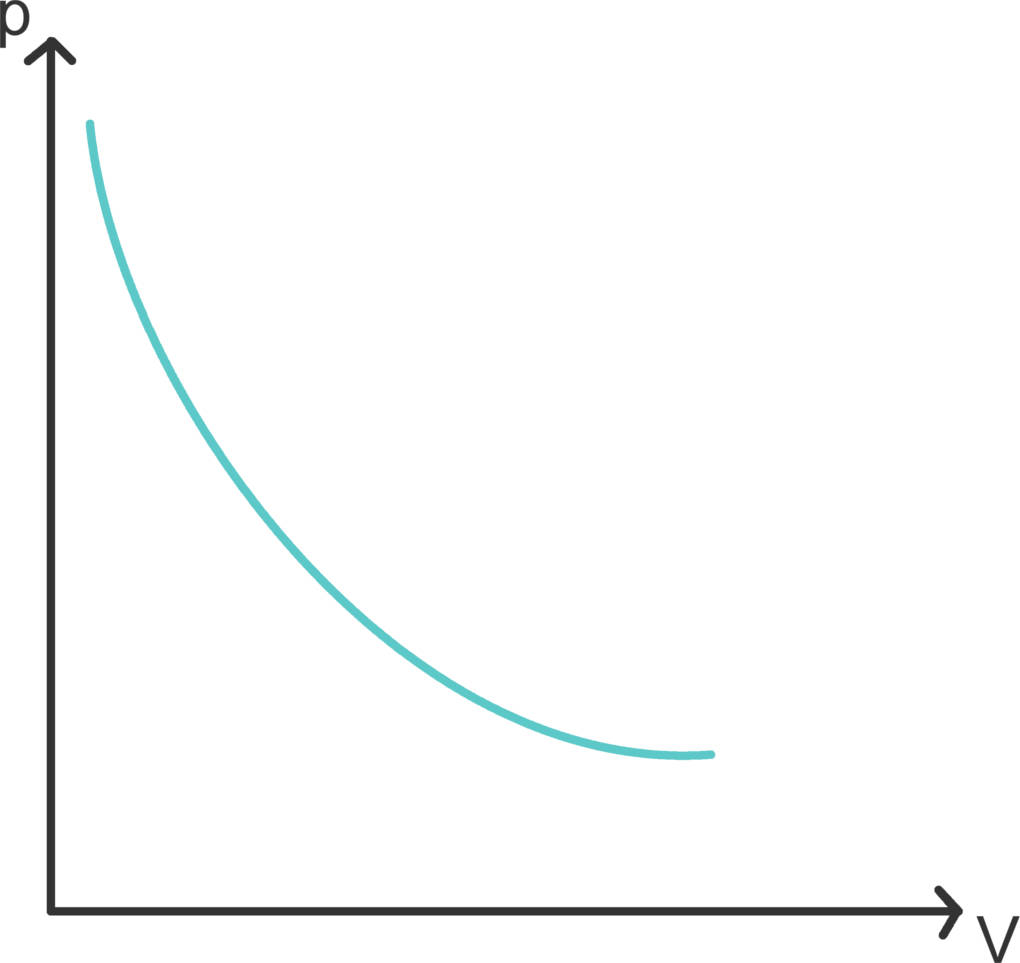
Isotherme Zustandsänderungen
Eine isotherme Zustandsänderung ist ein Prozess bei konstanter Temperatur. Im Carnot-Kreisprozess sind die Prozesse, die im Wärme- bzw. Kältereservoir stattfinden, isotherme Prozesse. In der Praxis ist es schwer bis unmöglich, die Temperatur konstant zu halten, allerdings ist es eine gute Näherung, wenn du etwas sehr langsam ausführst. Das langsame Auseinanderziehen einer Spritze ist beispielsweise isotherm.
Im Diagramm sind Isotherme Hyperbeln. Da die Temperatur ein Maß für die innere Energie eines Systems ist, bleibt auch die innere Energie bei einer Zustandsänderung mit konstanter Temperatur unverändert und es gilt $\Delta W=-\Delta Q$.
Adiabatische Zustandsänderungen
Eine adiabatische Zustandsänderung ist ein Prozess, bei dem keine Wärme ausgetauscht wird. Jede verrichtete Arbeit an einem solchen System entspricht demnach sofort der Zu- oder Abnahme der inneren Energie: $\Delta E=\Delta W$.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Thermodynamische Prozesse (14 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Thermodynamische Prozesse (5 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt





















 Carnotscher Kreisprozess
Carnotscher Kreisprozess
 Isochore Zustandsänderungen
Isochore Zustandsänderungen
 Isobare Zustandsänderungen
Isobare Zustandsänderungen
 Isotherme Zustandsänderungen
Isotherme Zustandsänderungen
 Adiabatische Zustandsänderungen
Adiabatische Zustandsänderungen









