Geometrische Körper, Schrägbilder und Netze
Zylinder, Kegel, Kugeln und Pyramiden sind unterschiedliche geometrische Körper. Hier erfährst du mehr über ihre Merkmale wie Flächen, Schrägbild, Volumen, Ecken und Kanten.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was sind geometrische Körper?
- Welche Eigenschaften besitzt der Zylinder?
- Zylinderförmige Gegenstände im Alltag
Was sind geometrische Körper?
Zylinder, Kegel, Pyramiden und Kugeln sind geometrische Körper und sie begegnen dir daher in der Geometrie sehr häufig. Körper bedeutet, dass es sich hierbei um Gegenstände handelt, die einen Raum einnehmen. Sie sind also dreidimensional.
Der Zylinder, der Kegel, die Pyramide und die Kugel unterscheiden sich in ihrem Aussehen und ihren Eigenschaften. Zu den Merkmalen von Körpern gehört, dass sie sich in der Anzahl ihrer Flächen, Ecken und Kanten unterscheiden.
Es gibt verschiedene Darstellungsformen von Körpern. Besonders wichtig sind Schrägbilder und Körpernetze, die dabei helfen die Körper in ihrer Räumlichkeit gut zu erfassen bzw. ihren Aufbau übersichtlich darzustellen.
Welche Eigenschaften besitzt der Zylinder?
Ein Zylinder wird aus drei Flächen zusammengesetzt:
- Eine Fläche hat die Form eines Rechtecks und wird Mantel genannt.
- Die zwei übrigen Formen sind zwei identische (also gleich große) Kreise, die parallel zueinander liegen. Diese Kreise bilden die Grund- und Deckfläche des Zylinders.
Die Übergänge von den Kreisen zu dem Rechteck werden als Kanten bezeichnet. Ein Zylinder hat somit zwei Kanten, aber keine Ecken. In der folgenden Abbildung kannst du links das Schrägbild und rechts das Netz eines Zylinders sehen.

Zylinderförmige Gegenstände im Alltag
Wenn du dich zu Hause oder draußen einmal umschaust, wirst du entdecken, dass es in deiner Umwelt viele zylinderförmige Gegenstände gibt. Dabei könntest du folgende Entdeckungen machen:
- Toilettenpapier- oder Küchenrollen haben die Form eines Zylinders. Wenn du eine Lage abrollst, erhältst du die Mantelfläche und siehst so, dass sie rechteckig ist.
- Weil Konservendosen praktisch sein und leicht zu stapeln sein müssen, haben sie die Form eines Zylinders. Eine solche Dose kannst du im folgenden Bild sehen:

- Vor allem in Städten findest du Litfaßsäulen, auf denen Werbung für Konzerte, Filme oder andere Events gemacht wird. In ihrer einfachsten Ausführung hat die Litfaßsäule die Form eines Zylinders.
- Auch manche Gläser haben ungefähr die Form eines Zylinders. Sie haben aber nur eine Grund- und keine Deckfläche. Wenn sie eine Deckfläche hätten, könntest du nicht mehr daraus trinken.
Welche Eigenschaften besitzt der Kegel?
Die Grundfläche eines Kegels ist ein Kreis. Die spitze Form des Kegels entsteht dadurch, dass jeder Punkt des Kreisrandes mit der Spitze des Kegels verbunden wird. Somit besteht ein Kegel aus den folgenden zwei Flächen:
- Die Grundfläche ist ein Kreis.
- Der Mantel ist ein Kreisausschnitt.
Die folgende Abbildung zeigt dir links das Schrägbild und rechts das Netz eines Kegels.
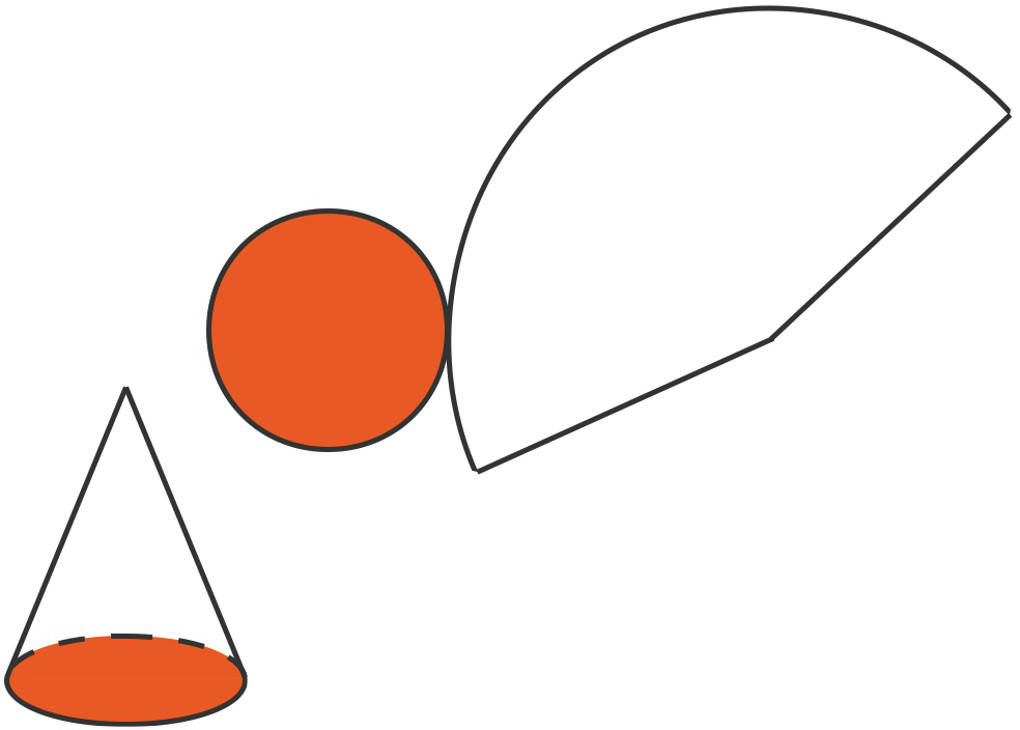
Somit hat ein Kegel nur eine Kante: der Übergang von der Grundfläche zum Mantel. Außerdem hat er eine Spitze.
Kegelförmige Gegenstände im Alltag
Du fragst dich bestimmt, wo du Kegel in deiner Umgebung finden kannst.

- Wenn du im Sommer zum Eiscafé gehst, kannst du die Kugeln Eis in einer Waffel bestellen. Diese Waffel (oder Eistüte) hat die Form eines Kegels.
- Bei deiner Einschulung hast du vielleicht eine Schultüte mit Süßigkeiten und nützlichen Dingen für die Schule bekommen. Auch eine solche Schultüte hat oft die Form eines Kegels.
Welche Eigenschaften besitzt die Pyramide?
Ähnlich wie ein Kegel hat auch die Pyramide eine Spitze. Sie setzt sich aus folgenden Flächen zusammen:
- Die Grundfläche kann ein Quadrat oder Dreieck sein.
- Jeder Eckpunkt der Grundfläche wird mit der Spitze der Pyramide verbunden. Dadurch entstehen dreieckige Seitenflächen.
Hier kannst du eine Pyramide mit quadratischer Grundfläche sehen, links ein Schrägbild und rechts das Netz einer Pyramide:

Anhand des Bildes kannst du einige Eigenschaften bestimmen. Eine quadratische Pyramide besteht aus fünf Flächen: die quadratische Grundfläche sowie vier gleichschenklige kongruente Dreiecke. Die vier Ecken der quadratischen Grundfläche sowie die Spitze ergeben insgesamt fünf Ecken. Die quadratische Grundfläche hat vier Kanten als Übergang zu den Dreiecken an den Seiten. Jeweils zwei Dreiecke haben eine gemeinsame Kante. Zusammen hat eine Pyramide also acht Kanten.
Pyramidenförmige Gegenstände im Alltag
Wo findest du Pyramiden in deiner Umgebung?
- Die Dächer von Kirchtürmen haben oft die Form einer Pyramide.
- Sicher hast du auch schon einmal von den ägyptischen Pyramiden gehört oder Bilder von diesen Pyramiden gesehen. Schon die alten Ägypter kannten die geometrische Form der Pyramide.
Welche Eigenschaften besitzt die Kugel?
Eine Kugel hat im Unterschied zu den vorigen Körpern keine Ecken und keine Kanten. Sie hat nur eine Fläche. Das Netz einer Kugel kann nicht gezeichnet werden:

Kugelförmige Gegenstände im Alltag
Kugeln findest du ziemlich häufig:
- Im Eiscafé kannst du eine oder mehrere Kugeln Eis mit deinen Lieblingssorten kaufen.
- Es gibt viele Ballsportarten, die einen kugelförmigen Ball verwenden: Handball, Tischtennis, Fußball oder Golf.
- Der Planet Erde, auf dem wir leben, hat auch die Form einer Kugel.
Was ist ein Körpernetz?
Ein Körpernetz bzw. eine Auffaltung ist eine ebene Darstellung eines geometrischen Körpers. Dabei wird dieser, wie der Name schon sagt, aufgefaltet. Die den Körper begrenzenden Seitenflächen liegen bei dieser Darstellung alle in einer Ebene nebeneinander. Um dir das besser vorstellen zu können, siehst du hier ein erstes Beispiel. Du willst deiner Tante Annemarie zum Geburtstag eine kleine Freude machen. Da sie sehr musikbegeistert und etwas altmodisch ist, sammelt sie CDs. Deshalb planst du, ihr aus Pappe eine Kiste für ihre neuesten Stücke zu basteln. Als Vorlage möchtest du das folgende Bild verwenden.

Anders als auf dem Bild möchtest du jedoch, dass die Kiste oben geschlossen ist. Die CD-Kiste soll also die Form eines Quaders haben. Wenn du die abgebildete Kiste an den zur Öffnung zeigenden Kanten aufschneidest und dir den Deckel dazu denkst, könnte das Ergebnis so aussehen.

Dies ist ein Körpernetz eines Quaders. Mit Hilfe dieses Körpernetzes kannst du nun die Oberfläche des Körpers berechnen. Das funktioniert, indem du den Flächeninhalt des Körpernetzes ausrechnest.
Wie wird ein Körpernetz mit Hilfe eines Körpers erstellt?
Hier lernst du, wie man aus einem Körper ein Körpernetz erstellen kann. Als Beispielfigur wird dabei ein Würfel, wie du ihn eventuell aus Brettspielen kennst, verwendet.

Die Abrollmethode
Wir nutzen nun einen solchen Würfel, um das Körpernetz eines Würfels zu erstellen. Dazu wenden wir folgende Schritte an:
- Lege diesen Würfel auf ein Blatt Papier und zeichne die Umrisse der Fläche ab, die auf dem Papier liegt.
- Merke dir die Zahl, die oben liegt, und rolle den Würfel zu einer beliebigen Seite.
- Schreibe in die gerade frei gewordene Fläche die gemerkte Zahl und zeichne wieder den Umriss der Fläche, die jetzt auf dem Papier liegt.
- Wiederhole nun Schritt 2 und 3 solange, bis du alle Augenzahlen des Würfels auf dem Papier hast.
Sobald du diese Schritte ausgeführt hast, erhältst du ein Würfelnetz. Im folgenden Bild kannst du ein solches Netz sehen.
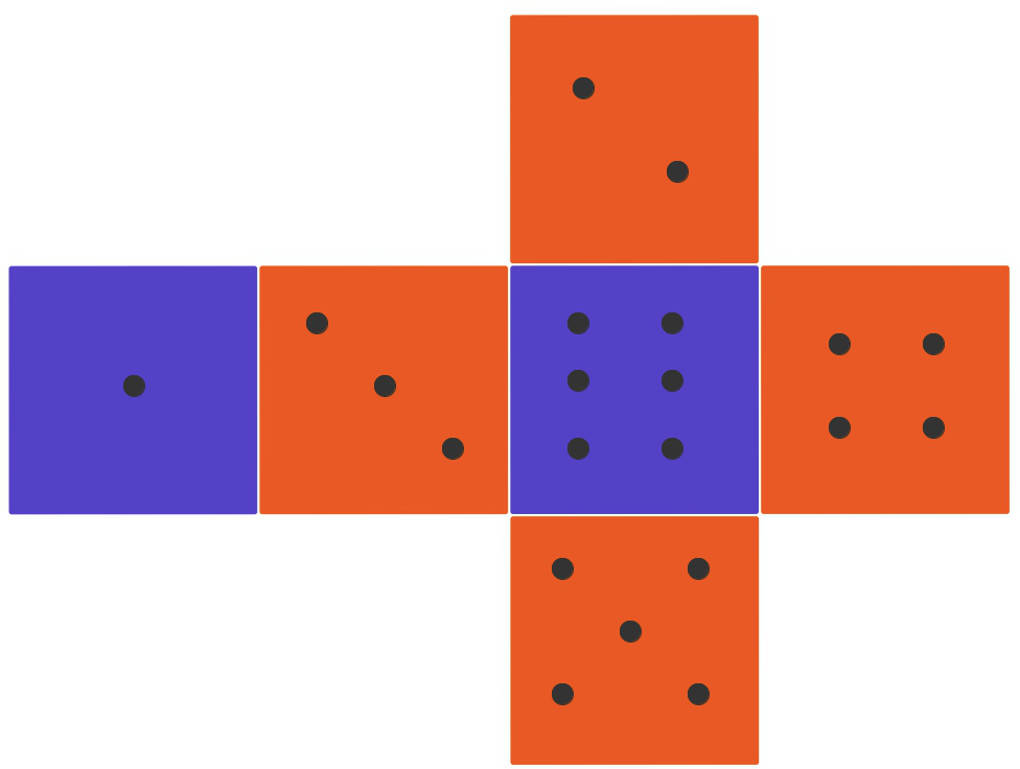
Ein Körper kann verschiedene Körpernetze haben
Im 2. Schritt der obigen Anleitung wird nicht festgelegt in welche Richtung du den Würfel rollen musst. Da du diesen Schritt mehrmals anwenden musst, können also verschiedene Netze entstehen, obwohl du ein und denselben Würfel benutzt. Alle diese Netze bestehen aus sechs Quadraten. Allerdings ist nicht jede Anordnung von sechs Quadraten ein Körpernetz eines Würfels. Hier siehst du einige Beispiele. Bei den beiden linken Anordnungen handelt es sich um Würfelnetze bei der rechten jedoch nicht.
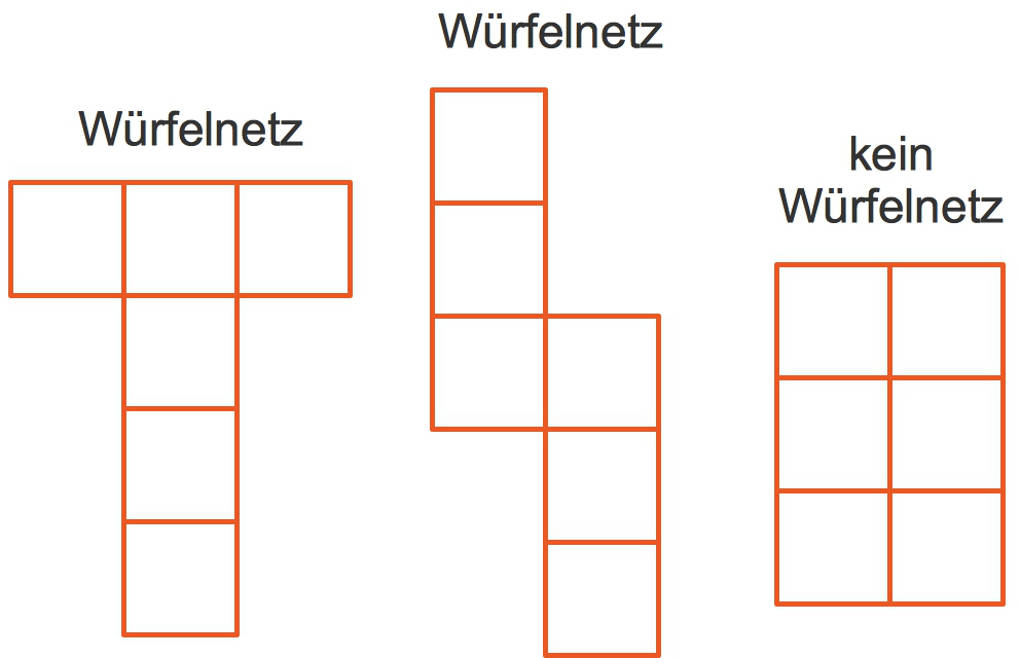
Es gibt übrigens insgesamt 11 verschiedene Würfelnetze. Probier doch mal aus, ob du noch welche findest. Verwende dazu die Abrollmethode.
Berechnung der Oberfläche von Körpern mit Hilfe von Körpernetzen
In den folgenden Absätzen findest du verschiedene Körper und die zugehörigen Netze. Zusätzlich wird dazu noch die Oberfläche des jeweiligen Körpers berechnet. Außerdem wird ein bekanntes Element aus dem Erdkunde-Unterricht als Beispiel für einen Körper gezeigt, für den man nicht ohne Probleme ein Netz zeichnen kann.
Würfel
Aus der Abrollmethode kennst du bereits das Körpernetz eines Würfels. Hier wird nun auch noch gezeigt, wie die Oberfläche eines Würfels berechnet wird. Die 6 Seitenflächen eines Würfels sind, wie man auch an dem zugehörigen Netz erkennen kann, jeweils Quadrate. Der Flächeninhalt A eines Quadrates mit der Seitenlänge $a$ berechnet sich durch A = $a^{2}$. Also ergibt sich für die Oberfläche O des Würfels O = 6 $\cdot a^{2}$.
Quader
Auch das Körpernetz eines Quaders kennst du bereits. Diese Form soll ja die Kiste für Tante Annemaries CDs haben. Hier siehst du ein Netz eines Quaders mit Bezeichnungen für die Seiten.
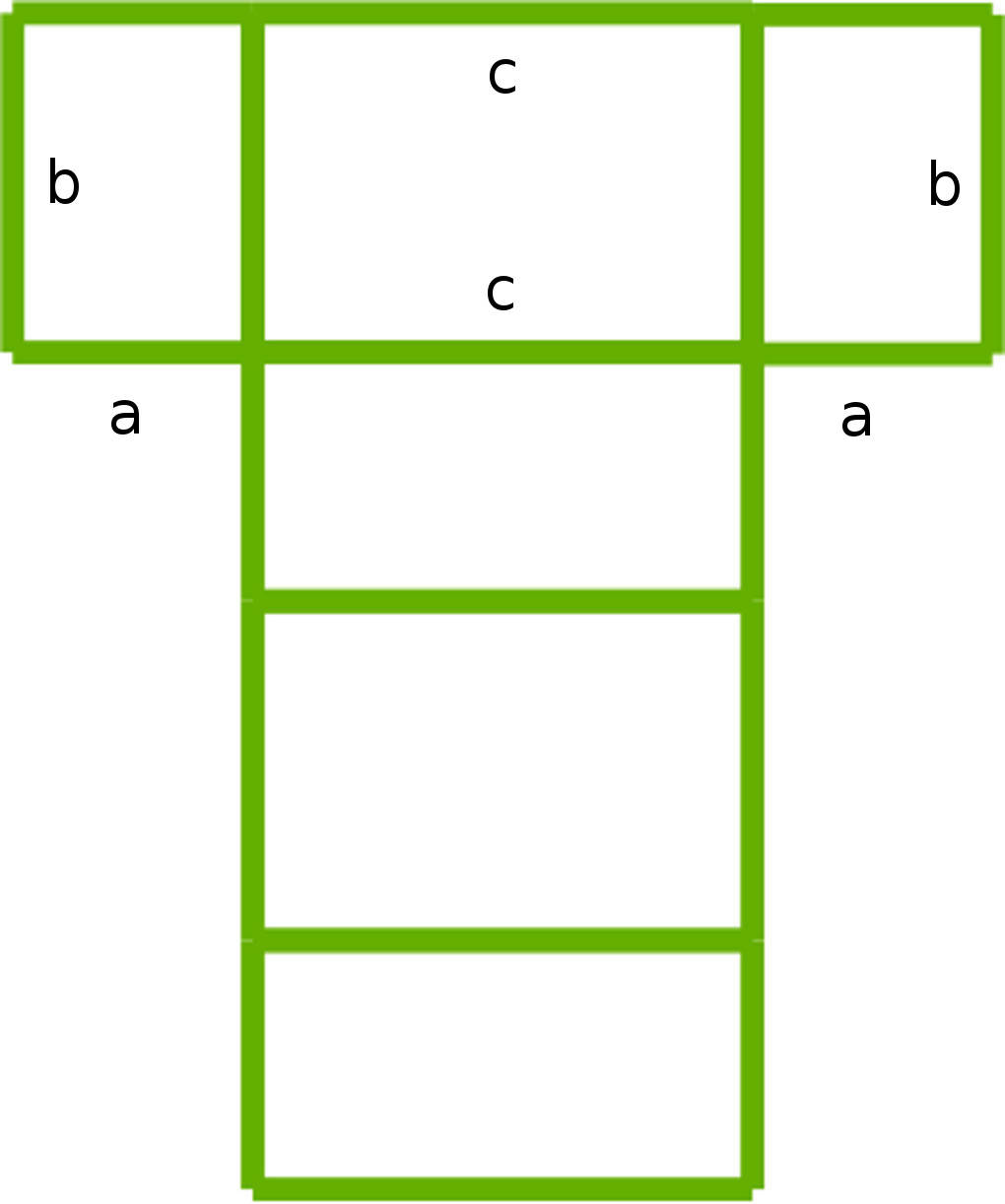
Nun siehst du, wie du die Oberfläche eines Quaders berechnen kannst. Wie in der Abbildung zu erkennen ist, besteht das Körpernetz eines Quaders aus 6 verschiedenen Rechtecken. Davon lassen sich jeweils 2 zusammenfassen, da sie kongruent (flächengleich) sind. Der Flächeninhalt jedes Rechtecks berechnet sich durch die Multiplikation der jeweiligen Seitenlängen. Insgesamt erhältst du für den Oberflächeninhalt O des Quaders O = 2ab + 2ac + 2bc = 2 $\cdot$ ( ab + ac + bc ).
Anwendungsaufgabe Körpernetz Quader: Die CD-Kiste
Der Geburtstag von Tante Annemarie rückt immer näher und du möchtest nun mit dem Basteln anfangen. Um entscheiden zu können, wie viel Pappe du brauchst, nimmst du eine CD-Hülle und misst diese aus:
- Breite:14,2 cm
- Höhe: 12,5 cm
- Tiefe: 1 cm
Die Kiste soll groß genug für 20 CDs sein. Du zeichnest dir eine Skizze mit Hilfe des Körpernetzes für Quader und schreibst die passenden Größen an die jeweiligen Seiten.
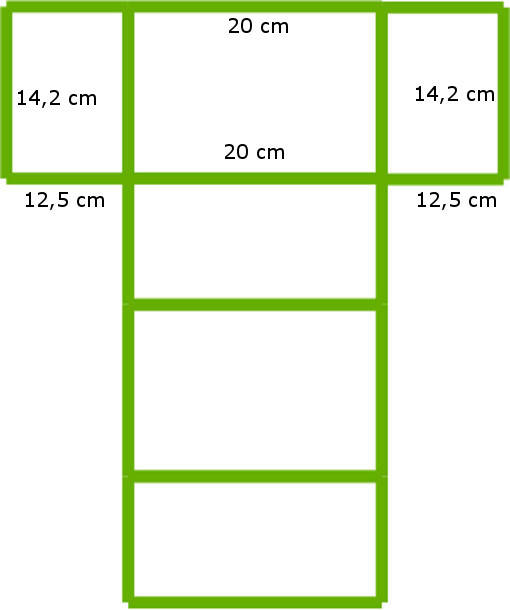
Die Oberflächen wird berechnet durch 2 $\cdot$ ( 20 $\cdot$ 14,2 + 20 $\cdot$ 12,5 + 14,2 $\cdot$ 12,5 ) = 1.423. Du brauchst also 1.423 $\text{ cm}^2$ Pappe.
Gegenbeispiel Körpernetz Kugel (Globus)
Eine Kugel ist ebenfalls ein mathematischer Körper. Du kennst diesen Körper eventuell aus dem Erdkundeunterricht. Ein Globus (lateinisches Wort für Kugel) stellt dort ein kugelförmiges Modell der Erde dar. Im Bezug auf Körpernetze stellt die Kugel eine Besonderheit dar: Durch die Krümmung der Kugel ist es nicht möglich, ein überlappungsfreies Körpernetz dieses Körpers zu erstellen.

Alle Videos zum Thema
Videos zum Thema
Geometrische Körper, Schrägbilder und Netze (16 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Geometrische Körper, Schrägbilder und Netze (16 Arbeitsblätter)
-
 Eigenschaften von Körpern
PDF anzeigen
Eigenschaften von Körpern
PDF anzeigen -
 Was ist der Unterschied zwischen Körper und Fläche?
PDF anzeigen
Was ist der Unterschied zwischen Körper und Fläche?
PDF anzeigen -
 Was ist eine Ecke?
PDF anzeigen
Was ist eine Ecke?
PDF anzeigen -
 Was ist eine Seitenfläche?
PDF anzeigen
Was ist eine Seitenfläche?
PDF anzeigen -
 Was ist ein Würfel?
PDF anzeigen
Was ist ein Würfel?
PDF anzeigen -
 Was ist ein Quader?
PDF anzeigen
Was ist ein Quader?
PDF anzeigen -
 Was ist ein Zylinder?
PDF anzeigen
Was ist ein Zylinder?
PDF anzeigen -
 Die Pyramide
PDF anzeigen
Die Pyramide
PDF anzeigen -
 Der Kegel
PDF anzeigen
Der Kegel
PDF anzeigen -
 Die Kugel
PDF anzeigen
Die Kugel
PDF anzeigen -
 Was ist eine Kante?
PDF anzeigen
Was ist eine Kante?
PDF anzeigen -
 Wie unterscheiden sich Zylinder und Kegel voneinander?
PDF anzeigen
Wie unterscheiden sich Zylinder und Kegel voneinander?
PDF anzeigen -
 Würfelnetze
PDF anzeigen
Würfelnetze
PDF anzeigen -
 Quadernetze
PDF anzeigen
Quadernetze
PDF anzeigen -
 Pyramidennetze
PDF anzeigen
Pyramidennetze
PDF anzeigen -
 Zylindernetze
PDF anzeigen
Zylindernetze
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter































