Terme aufstellen, umformen und berechnen
Terme sind Rechenausdrücke. In diesen kommen Zahlen, Variablen und Rechenzeichen vor. Ein solcher Rechenausdruck muss sinnvoll sein. Wenn du eine Textaufgabe bearbeiten möchtest, musst du Terme aufstellen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist ein Term?
Ein Term ist ein sinnvoller Rechenausdruck, in welchem
- Zahlen,
- Variablen,
- Rechenzeichen und
- Klammern vorkommen.
In einem Term kommen KEINE
- Gleichheitszeichen ($=$) oder
- Relationszeichen ($>$, $\ge$, $<$, $\le$) vor.
Was bedeutet „sinnvoll“? Wenn du für die Variablen Zahlen einsetzt, kannst du den Wert des Terms berechnen.
Beispiele
- Eine Zahl oder eine Variable können durchaus alleine stehen. Sie sind dann auch ein Term, z.B. $x$ oder $5$. Ein Rechenzeichen allein ist kein Term.
- Du kannst ein Rechenzeichen auch als Vorzeichen, zum Beispiel $-3$ für eine negative Zahl, verwenden. Auch dies ist ein Term.
- Umgekehrt, also $3-$, liegt kein Term vor.
- $x+1$ ist ein Term. Er besteht aus der Variablen $x$, dem Rechenzeichen $+$ und der Zahl $1$. Wenn du zum Beispiel für $x=3$ einsetzt, erhältst du $3+1=4$.
- Terme können auch durchaus etwas umfangreicher sein: $3x\cdot (5-y)+(2+x)\cdot(-x+3)$ ist auch ein Term.
- Übrigens: $3x$ ist die abkürzende Schreibweise für $3\cdot x$. Da hier klar ist, dass multipliziert werden muss, lässt man häufig das $\cdot$-Zeichen weg. Dies darfst du allerdings nicht bei einem Produkt von Zahlen machen: $2\cdot 4\neq 24$.
Merkhilfe
In der folgenden Abbildung siehst du, wie „Term-Plätzchen“ gebacken werden. Auf der rechten Seite wurde sich scheinbar nicht an das Rezept gehalten, was du unten im Bild erkennen kannst.

Was sind ergebnisgleiche Terme?
Man spricht von ergebnisgleichen Termen, wenn die Terme, egal welche Werte für die Variablen eingesetzt werden, immer das gleiche Ergebnis haben.
Ergebnisgleiche Terme sind:
- $x+0$ und $x$, da die Addition von $0$ nichts an einem Term ändert. Du schreibst dann $x+0=x$.
- Auch $x+1$ und $1+x$ sind ergebnisgleich. Du weißt sicher, dass du beim Addieren die Reihenfolge der Summanden vertauschen darfst. Das bezeichnet man als das Kommutativgesetz der Addition. Auch hier schreibst du $x+1=1+x$.
- $3-x$ und $2-x+1$ sind ergebnisgleich, da die beiden Zahlen im rechten Term zu $3$ addiert werden können.
Nicht ergebnisgleich sind die folgenden Terme:
- $x-1$ und $1-x$, denn bei der Subtraktion darfst du Reihenfolge nicht vertauschen. Nehmen wir einmal an, die beiden Terme wären ergebnisgleich, dann kannst du für $x$ eine beliebige Zahl einsetzen und beide Terme haben den gleichen Wert. Probieren wir das doch einmal aus und setzen für $x=3$ ein: $3-1=2$ aber $1-3=-2$. Du siehst, die Ergebnisse stimmen nicht überein.
- $2x+2$ und $3x$ sind auch nicht ergebnisgleich. Zwar gilt für $x=2$, dass der linke Term $2\cdot 2+2=6$ und auch der rechte Term $3\cdot 2=6$ ergibt, jedoch sind die Ergebnisse für alle anderen Werte für $x$ nicht gleich. Zum Beispiel für $x=3$ ist $2\cdot 3+2=8$, aber $3\cdot 3=9$.
Aufstellen von Termen
Nachdem du nun weißt, was ein Term ist, lernst du nun, wie du einen solchen Term aufstellen kannst.
Das Aufstellen von Termen kannst du dir so vorstellen: Du hast eine Gegebenheit, welche du mit Hilfe von Zahlen und Variablen sowie Rechenzeichen und vielleicht auch Klammern darstellen sollst, ... also als Term.
Schauen wir uns ein Beispiel an.
Paul und seine Schwester
Paul ist $3$ Jahre älter als seine Schwester.
- Da das Alter von Pauls Schwester nicht bekannt ist, verwendest du die Variable $x$. Du hättest auch einen anderen Buchstaben verwenden können.
- Was bedeutet es nun, dass Paul $3$ Jahre älter ist als seine Schwester? Du musst zu dem Alter der Schwester, also $x$, die $3$ addieren.
- So kommst du zu dem Term $x+3$.
Wenn du nun das Alter von Pauls Schwester kennst, zum Beispiel $5$ Jahre, kannst du für $x=5$ einsetzen und erhältst für den Term den Wert $5+3=8$. Also ist Paul dann $8$ Jahre alt.
Der Umfang eines Rechtecks
Bei einem Rechteck ist bekannt, dass die längere Seite doppelt so lang ist wie die kürzere. Wir verwenden für die Länge der kürzeren Seite die Variable $x$.

Zunächst überlegen wir uns, was es bedeutet, dass die längere Seite doppelt so lang ist wie die kürzere. „Doppelt so lange“ entspricht der Multiplikation mit $2$. Also kann dies durch den Term $2x$ dargestellt werden.
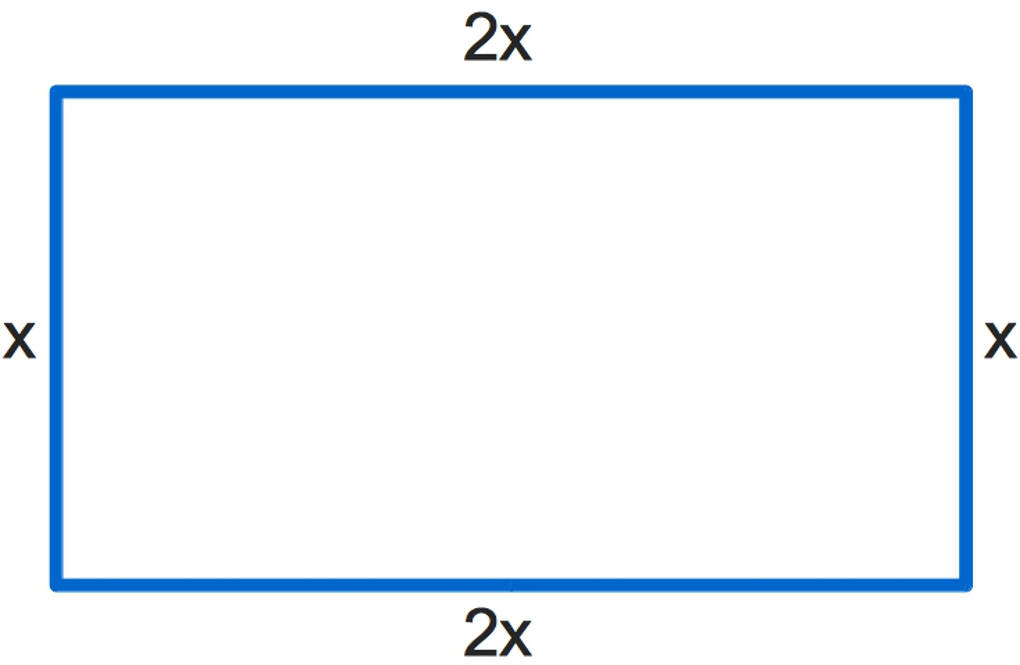
Sowohl die Variable $x$ selbst als auch $2x$ sind jeweils Terme.
Den Umfang des Rechtecks kannst du nun so berechnen:
- Du gehst einmal die Seite der Länge $x$ entlang und dann die Seite der Länge $2x$. Wie weit bist du bereits gegangen? Richtig: $x+2x$. Auch dies ist ein Term.
- Gehe nun noch einmal die Seite der Länge $x$. So erhältst du den Term $x+2x+x$.
- Zuletzt gehst du die Seite der Länge $2x$ entlang.
- Zusammen beträgt der Umfang also $x+2x+x+2x$. Dies ist ebenfalls ein Term.
Wenn du zu einem $x$ zwei weitere $x$ dazutust und dann noch ein $x$ und noch einmal zwei $x$, dann sind das zusammen $6x$. Nun hast du wieder einen Term gefunden.
Die beiden Terme $x+2x+x+2x$ und $6x$ sind ergebnisgleich: $x+2x+x+2x=6x$.
Du kannst für $x$ jeden beliebigen Wert einsetzen. Du erhältst immer das gleiche Ergebnis. Wir probieren das einmal für einige Werte:
- Für $x=4$ erhältst du $4+2\cdot4+4+2\cdot 4=24=6\cdot 4$.
- Für $x=12$ erhältst du $12+2\cdot12+12+2\cdot 12=72=6\cdot 12$.
- Für $x=5$ erhältst du $5+2\cdot5+5+2\cdot 5=30=6\cdot 5$.
- ...
Die Ergebnisgleichheit kannst du natürlich nicht durch Einsetzen nachweisen, dafür müsstest du unendlich viele Werte für $x$ einsetzen. Zum Nachweis formst du den Term wie folgt um.
$\begin{array}{rclcl} x+2x+x+2x&=&6x \\ 3x+x+2x&=&6x \\ 4x+2x&=&6x \\ 6x&=&6x&&|\div 6 \\ x&=&x \end{array}$
Damit ist die Ergebnisgleicheit der Terme eindeutig bewiesen.
Alle Videos zum Thema
Videos zum Thema
Terme aufstellen, umformen und berechnen (12 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Terme aufstellen, umformen und berechnen (12 Arbeitsblätter)
-
 Was ist ein Term?
PDF anzeigen
Was ist ein Term?
PDF anzeigen -
 Terme aufstellen und berechnen
PDF anzeigen
Terme aufstellen und berechnen
PDF anzeigen -
 Terme aufstellen – Anwendung
PDF anzeigen
Terme aufstellen – Anwendung
PDF anzeigen -
 Termumformungen ohne Variablen
PDF anzeigen
Termumformungen ohne Variablen
PDF anzeigen -
 Termumformungen mit Variablen
PDF anzeigen
Termumformungen mit Variablen
PDF anzeigen -
 Termumformungen (Übungsvideo)
PDF anzeigen
Termumformungen (Übungsvideo)
PDF anzeigen -
 Aus gegebenen Daten Terme aufstellen und berechnen
PDF anzeigen
Aus gegebenen Daten Terme aufstellen und berechnen
PDF anzeigen -
 Terme vereinfachen
PDF anzeigen
Terme vereinfachen
PDF anzeigen -
 Terme mit unterschiedlichen Variablen zusammenfassen
PDF anzeigen
Terme mit unterschiedlichen Variablen zusammenfassen
PDF anzeigen -
 Schlüsselwörter für Addition und Subtraktion
PDF anzeigen
Schlüsselwörter für Addition und Subtraktion
PDF anzeigen -
 Terme aufstellen und berechnen (Übungsvideo)
PDF anzeigen
Terme aufstellen und berechnen (Übungsvideo)
PDF anzeigen -
 Termumformungen mit mehreren Variablen
PDF anzeigen
Termumformungen mit mehreren Variablen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze


























